Непрерывность функции в точке и на числовом промежутке. Свойства непрерывных функций

Понятие непрерывности функции
Функция f(x) называется непрерывной в точке x0, если она определена в этой точке (т.е. существует значение
функции в этой точке f(x0)) и имеет конечный предел при
равный значению функции в этой точке:
определение 1.

Функция
не является непрерывной в точке х=0, т.к. не существует значения функции в этой точке:
ПРИМЕРЫ.
1

Функция
существует в точке х=0 , т.к. у(0)=1
2
Рассмотрим пределы этой функции в точке х=0 .
Предел слева:
Предел справа:
Эти пределы неравны, следовательно общего предела не существует и функция не является непрерывной в этой точке.

Функция
является непрерывной в точке х=0, т.к. существует значение функции в этой точке: y(0)=0
3
и существует предел

Определение непрерывности функции может быть записано в виде:
определение 2.

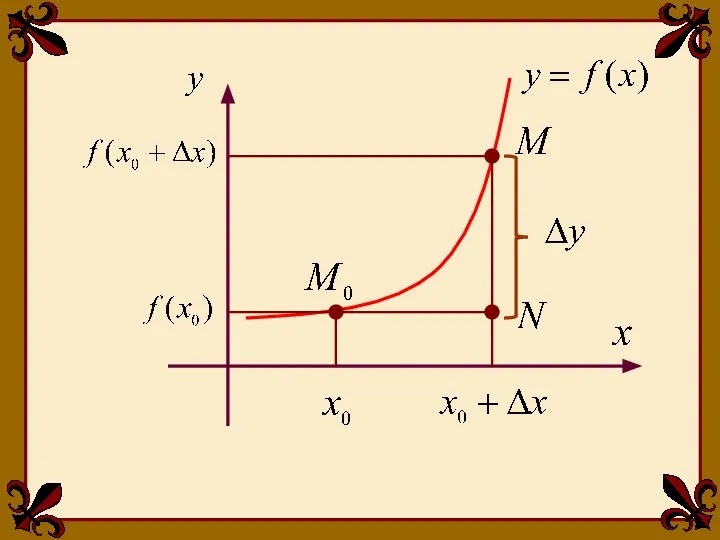
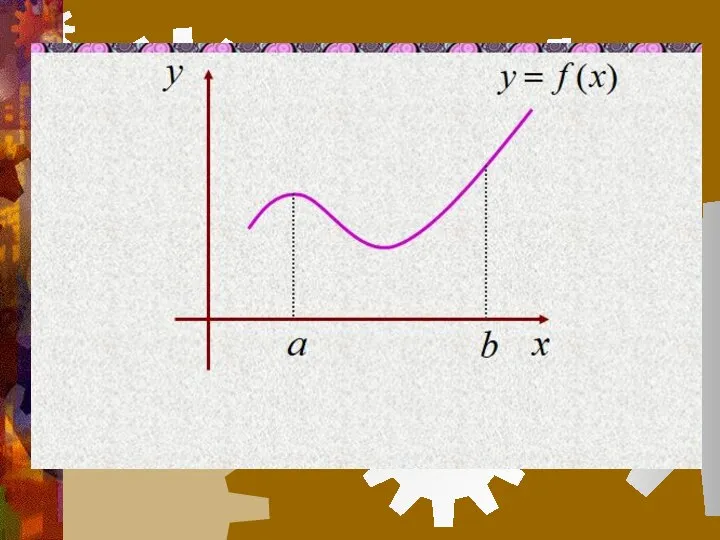
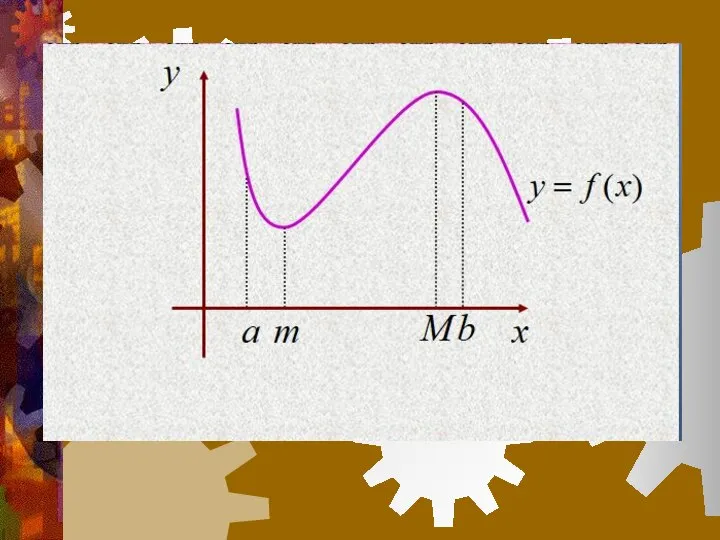
Непрерывность функции в данной точке выражается непрерывностью графика при прохождении этой точки.
Рассмотрим график функции y=f(x).
Дадим аргументу x0 приращение Δx. Тогда функция получит приращение Δy:
Графически:

определение 3.
Функция f(x) называется непрерывной в точке x0, если она определена в точке x0 и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:

Точка x0 называется точкой разрыва
функции f(x), если в этой точке функция
не является непрерывной.

Точка x0 называется точкой разрыва второго
рода функции f(x), если хотя бы один из
односторонних пределов функции равен
бесконечности или не существует.
Точка x0 называется точкой разрыва первого
рода функции f(x), если существуют
односторонние пределы функции слева и
справа при
Точки разрыва бывают 1 и 2 рода.

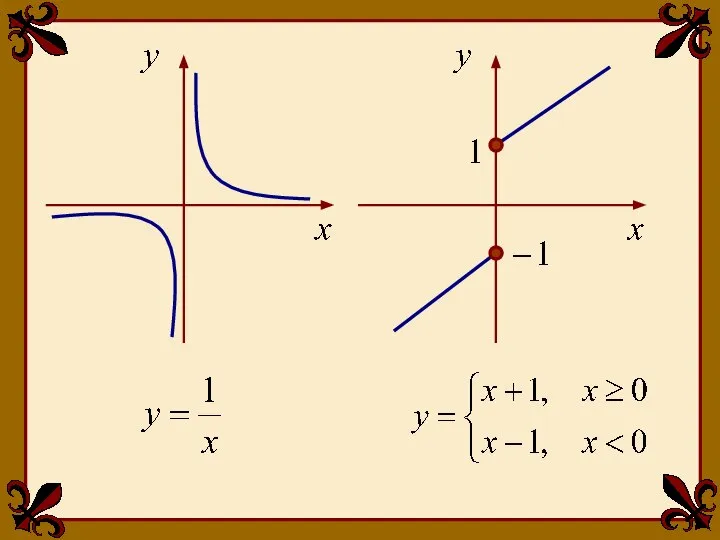
Функция
имеет точку разрыва второго рода х=0, поскольку:
ПРИМЕРЫ.
1

Функция
2
имеет точку разрыва первого рода х=0, поскольку:

1
тоже являются функциями, непрерывными в точке x0.
СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ В ТОЧКЕ