Содержание
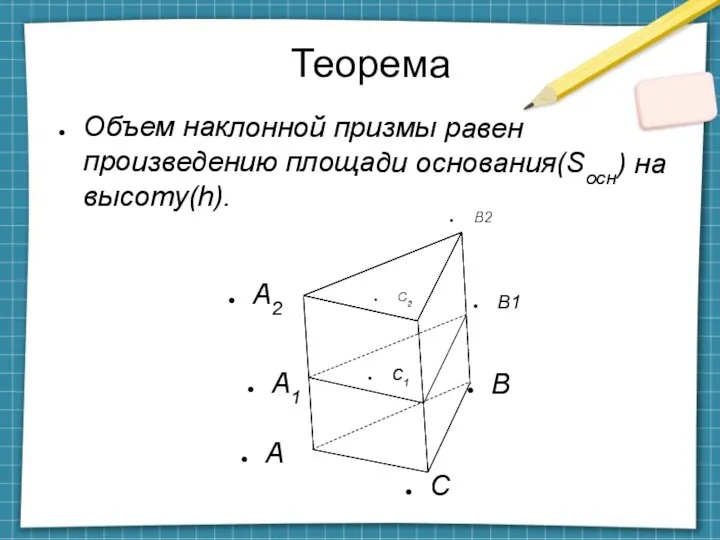
- 2. Теорема А Объем наклонной призмы равен произведению площади основания(Sосн) на высоту(h). C B А2 B1 А1
- 3. Докажем: А 1. Рассмотрим треугольную призму с объемом V. На одном из оснований поставим точку О,
- 4. Докажем: Таким образом треугольники A1B1C1 и ABC равны по 3 сторонам, ч.т.д. Следовательно, S(x)=S. Применяя теперь
- 6. Скачать презентацию


 Натуральные и целые числа. Проверочная работа
Натуральные и целые числа. Проверочная работа Арксинус и уравнение вида sinx=a
Арксинус и уравнение вида sinx=a Геометрия в живописи
Геометрия в живописи Основы моделирования
Основы моделирования Правильные многогранники
Правильные многогранники Прямоугольный треугольник
Прямоугольный треугольник Решение задач с применением раскрасок
Решение задач с применением раскрасок Логарифмические уравнения
Логарифмические уравнения Свойства предметов (часть 2)
Свойства предметов (часть 2) Графический способ решения систем уравнений
Графический способ решения систем уравнений Практические задания на применение формул сокращённого умножения
Практические задания на применение формул сокращённого умножения Интерактивный тренажёр. 4 класс
Интерактивный тренажёр. 4 класс Альтернативные издержки и кривая производственных возможностей
Альтернативные издержки и кривая производственных возможностей Сравнение чисел
Сравнение чисел Устный счет. Пропорция
Устный счет. Пропорция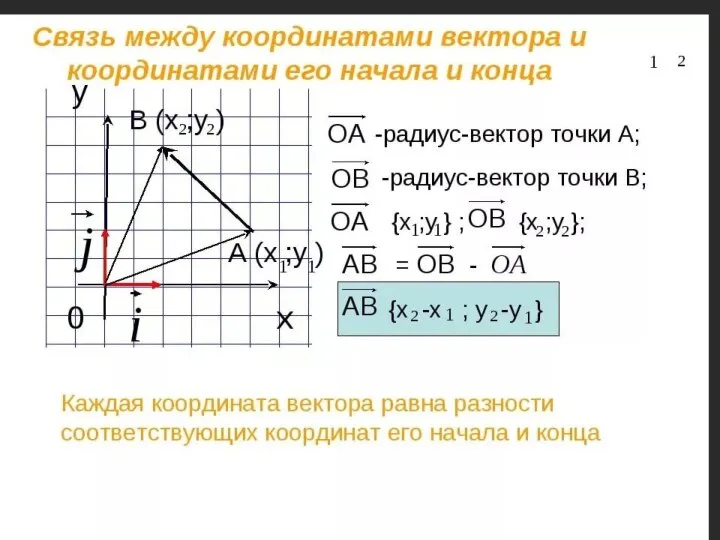 Векторы
Векторы Понятие логарифма
Понятие логарифма Игра
Игра Параллельные прямые
Параллельные прямые Сложение однозначных чисел с переходом через десяток вида +8, +9 (часть 1)
Сложение однозначных чисел с переходом через десяток вида +8, +9 (часть 1) Аналитическая панель
Аналитическая панель Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения Цифровые устройства. Логические функции и их минимизация
Цифровые устройства. Логические функции и их минимизация Составление переводной работы по алгебре в формате ЕГЭ, 2017-2018 учебный год
Составление переводной работы по алгебре в формате ЕГЭ, 2017-2018 учебный год Золотое сечение
Золотое сечение Булева алгебра
Булева алгебра Дифференциальные уравнения
Дифференциальные уравнения Степень с отрицательным показателем
Степень с отрицательным показателем