Содержание
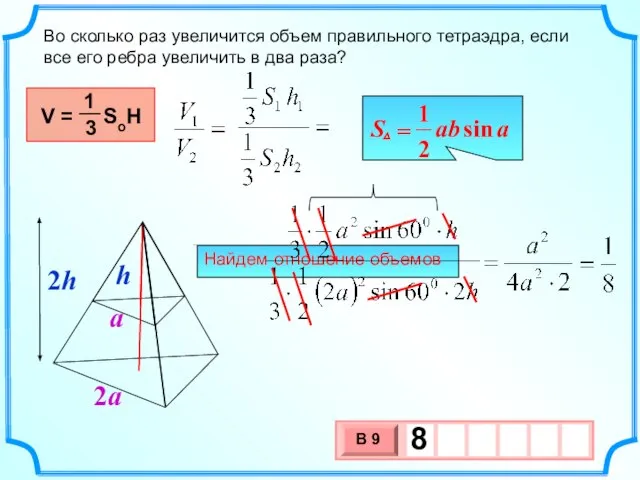
- 2. Найдем отношение объемов Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в
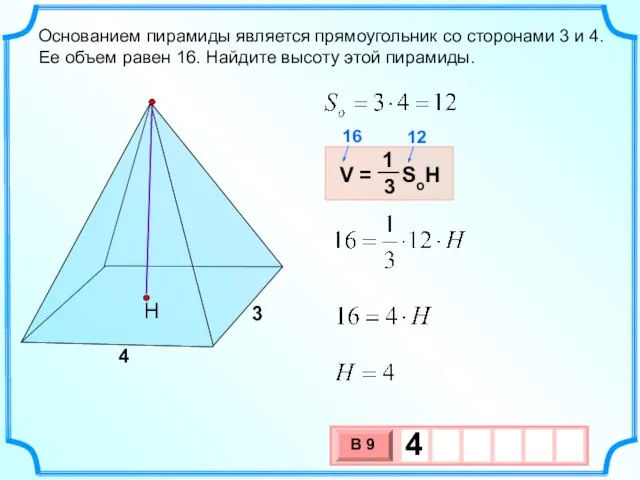
- 3. Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой
- 4. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна . 1 1
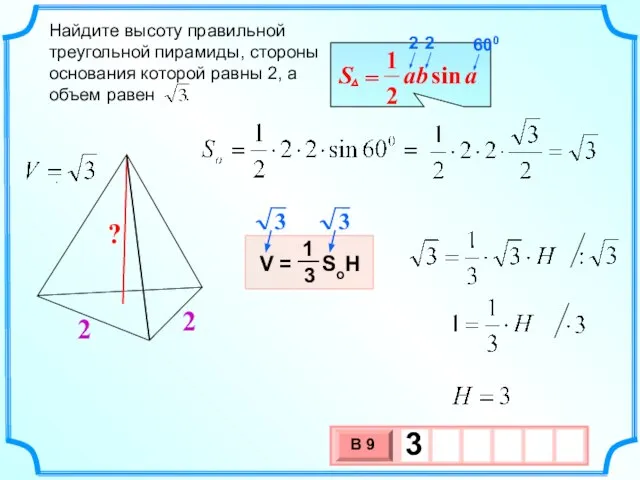
- 5. . Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен . 2
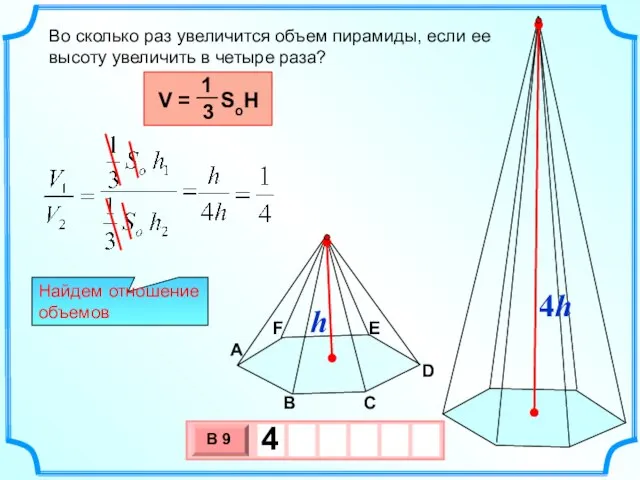
- 6. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза? Найдем отношение объемов
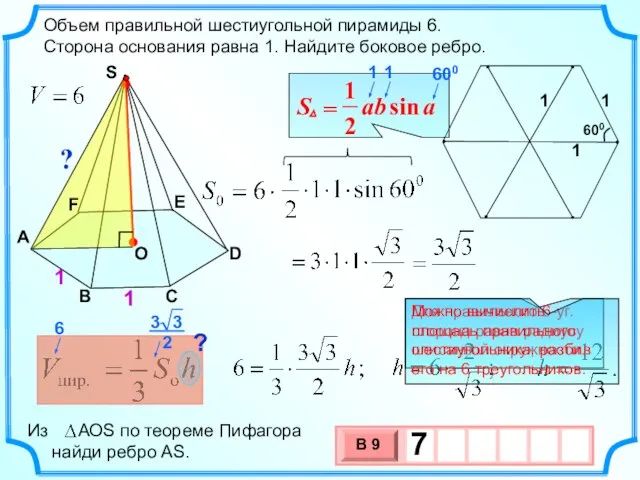
- 7. . Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро. A F B
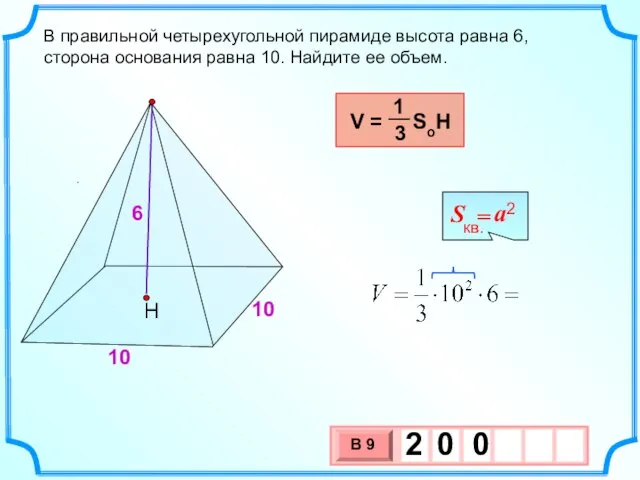
- 8. . В правильной четырехугольной пирамиде высота равна 6, сторона основания равна 10. Найдите ее объем. 6
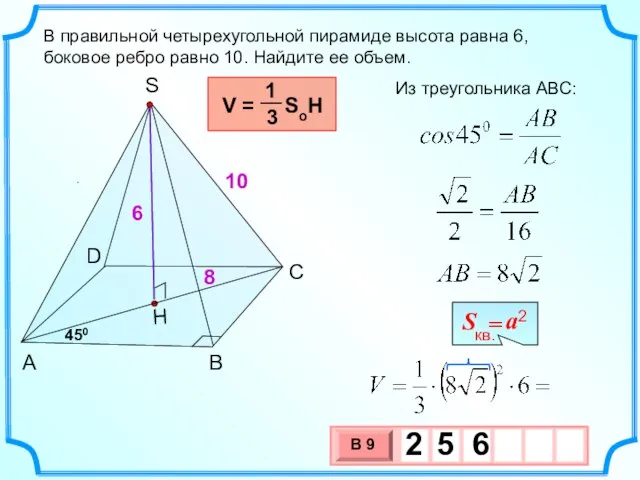
- 9. . В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем. 6
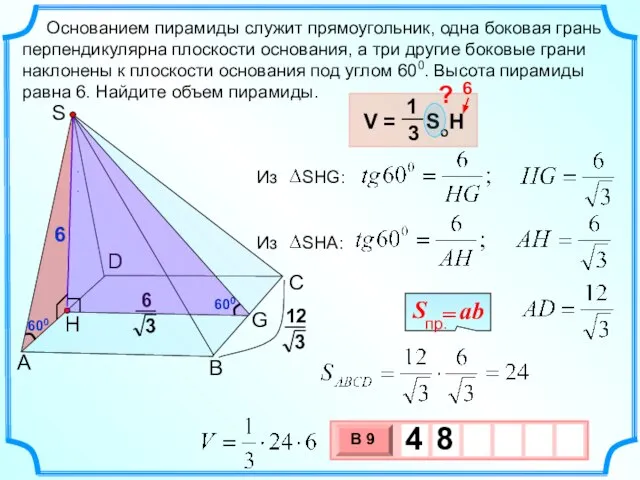
- 10. . Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани
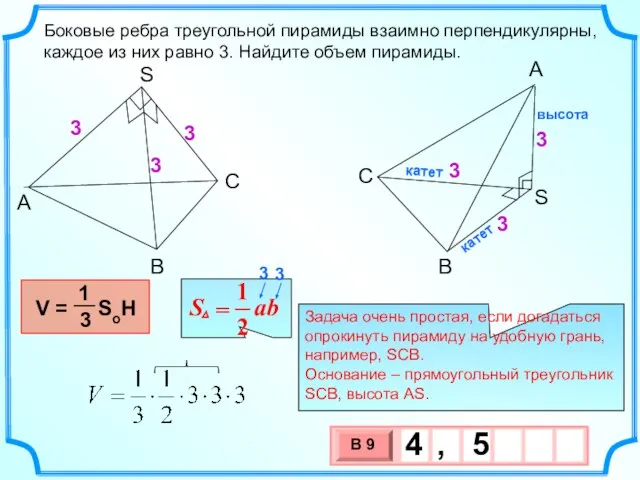
- 11. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды. Задача очень
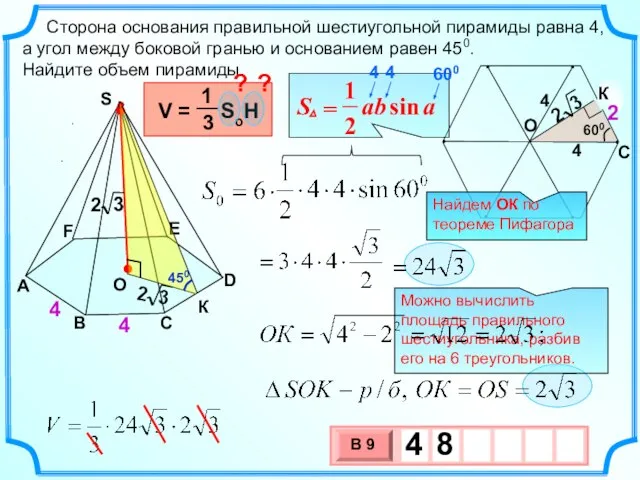
- 12. Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 450.
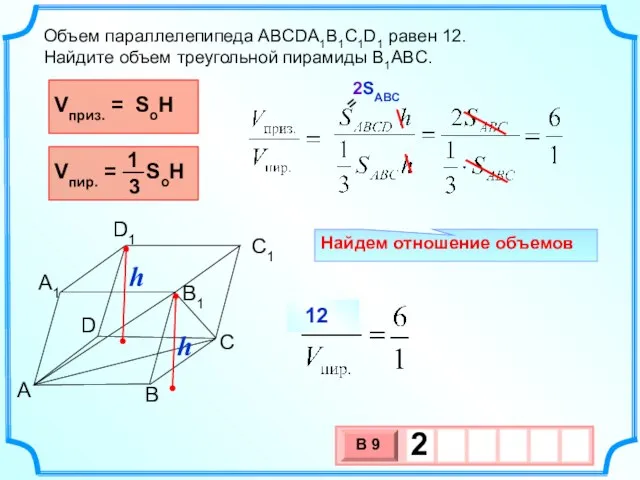
- 13. Найдем отношение объемов Объем параллелепипеда ABCDA1B1C1D1 равен 12. Найдите объем треугольной пирамиды B1ABC. B C D
- 14. Пирамида AD1CB1 получается, если мы отрежем от параллелепипеда четыре пирамиды по углам — ABCB1, D1B1CC1, AA1D1B1
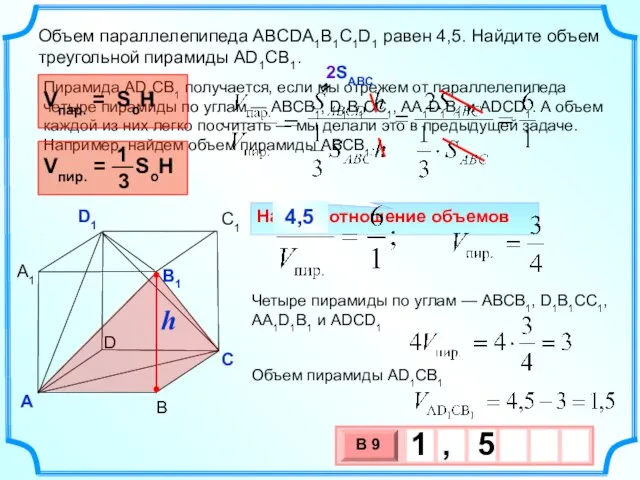
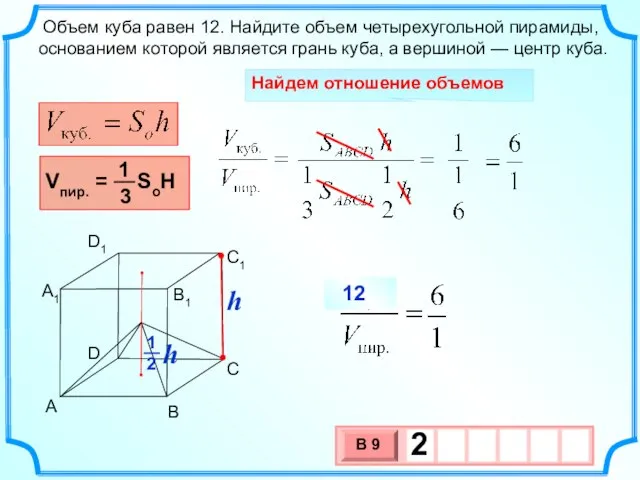
- 15. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной —
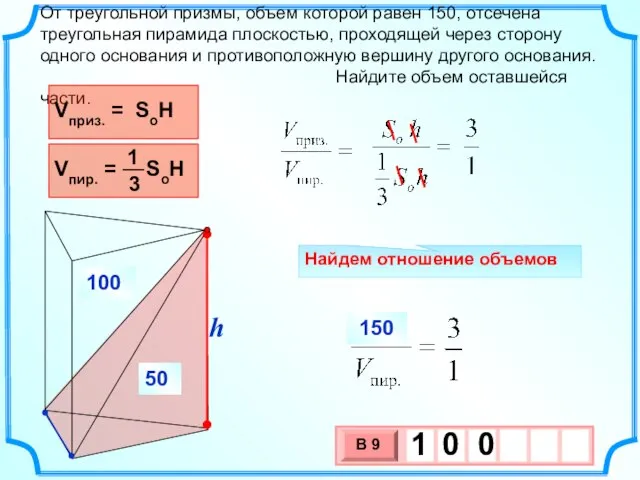
- 16. От треугольной призмы, объем которой равен 150, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания
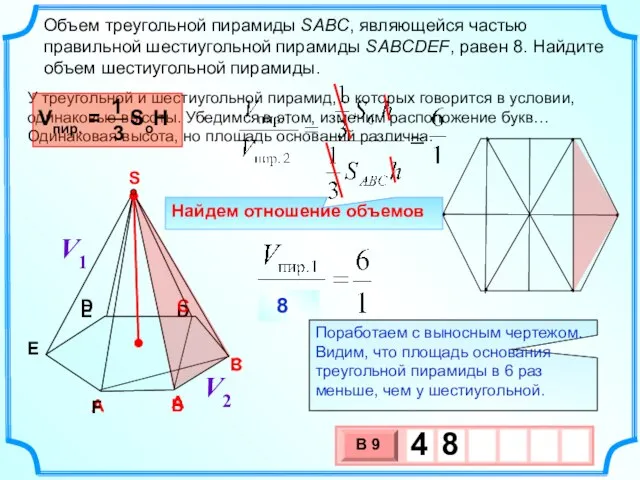
- 17. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 8. Найдите объем шестиугольной пирамиды.
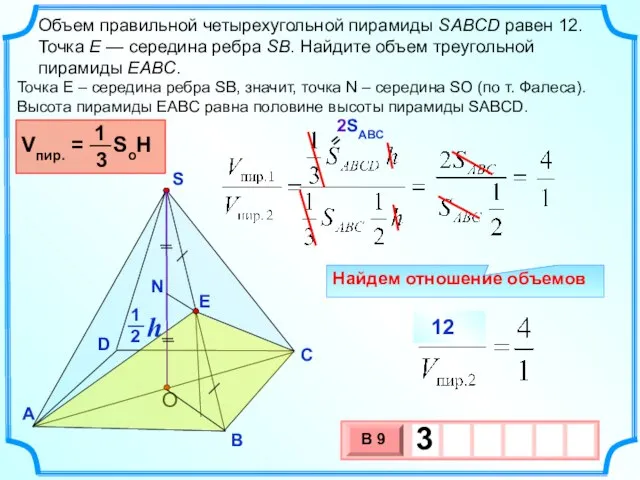
- 18. Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной
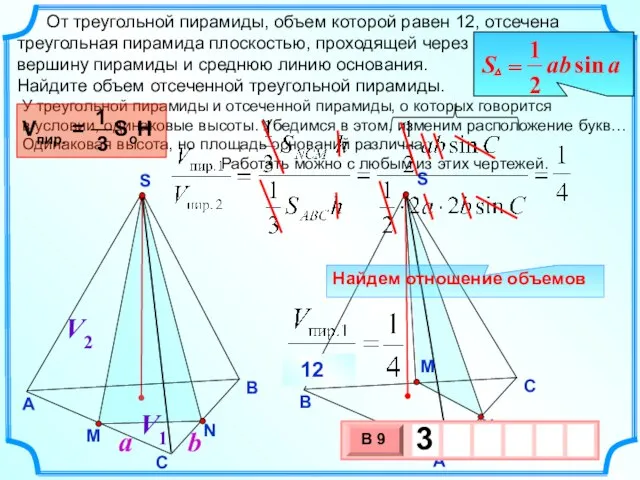
- 19. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и
- 21. Скачать презентацию

 Решение тригонометрических уравнений
Решение тригонометрических уравнений Алгоритм вычисления алгебраических выражений
Алгоритм вычисления алгебраических выражений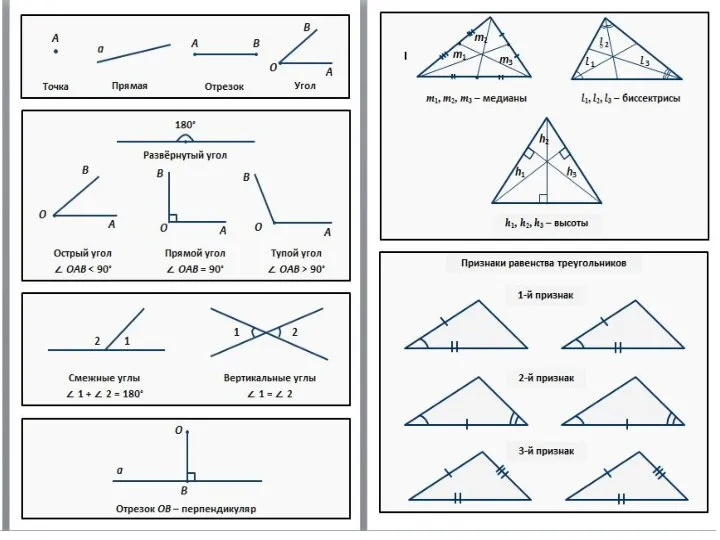 Геометрия. 8 класс
Геометрия. 8 класс Деление с остатком
Деление с остатком Понятие интеграла
Понятие интеграла Тема Функция у = ах2 и её график
Тема Функция у = ах2 и её график Конус. Виды конусов. Конусы в нашей жизни
Конус. Виды конусов. Конусы в нашей жизни Приближенные числа. Округление чисел. Бородино 1812 г. 26 августа (7 сентября)
Приближенные числа. Округление чисел. Бородино 1812 г. 26 августа (7 сентября) Способы решения тригонометрических уравнений
Способы решения тригонометрических уравнений polupravilnye-mnogogranniki
polupravilnye-mnogogranniki Решение показателей уравнений
Решение показателей уравнений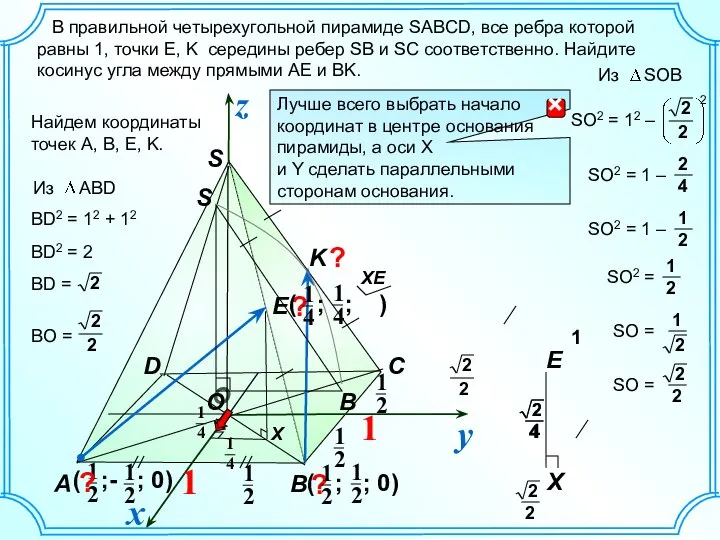 Пирамиды. Решение задач. C 12
Пирамиды. Решение задач. C 12 Примеры на сложение и вычитание
Примеры на сложение и вычитание Итоговое повторение. 9 класс (2)
Итоговое повторение. 9 класс (2) Геометрические фигуры: круг, квадрат, треугольник
Геометрические фигуры: круг, квадрат, треугольник Графы. ЕГЭ задание 15. Урок 11 А
Графы. ЕГЭ задание 15. Урок 11 А Математическая разминка
Математическая разминка Личные (семейные) финансы. Финансовое планирование и бюджет. Решение задач
Личные (семейные) финансы. Финансовое планирование и бюджет. Решение задач Вычисления с многозначными числами
Вычисления с многозначными числами Графики. График движения
Графики. График движения Движение по окружности. Подборка задач
Движение по окружности. Подборка задач Графическое оформление результатов эксперимента
Графическое оформление результатов эксперимента Введение в математический анализ и дифференциальное исчисление
Введение в математический анализ и дифференциальное исчисление Задачи на концентрацию, сплавы. Подготовка к ЕГЭ
Задачи на концентрацию, сплавы. Подготовка к ЕГЭ Сложение и вычитание в пределах 20. Повторение
Сложение и вычитание в пределах 20. Повторение Презентация по математике "Мы рады привествовать вас на уроке математики" -
Презентация по математике "Мы рады привествовать вас на уроке математики" -  Линейная алгебра. Метод Гаусса для решения систем линейных алгебраических уравнений
Линейная алгебра. Метод Гаусса для решения систем линейных алгебраических уравнений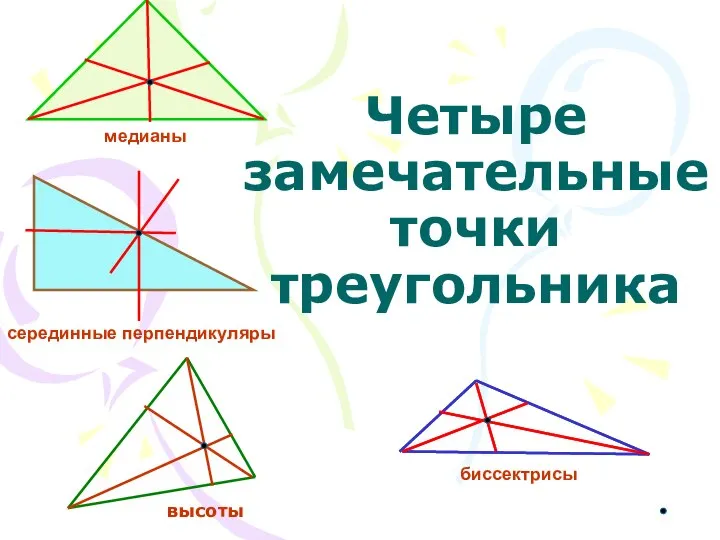 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника