Описанная окружность треугольника

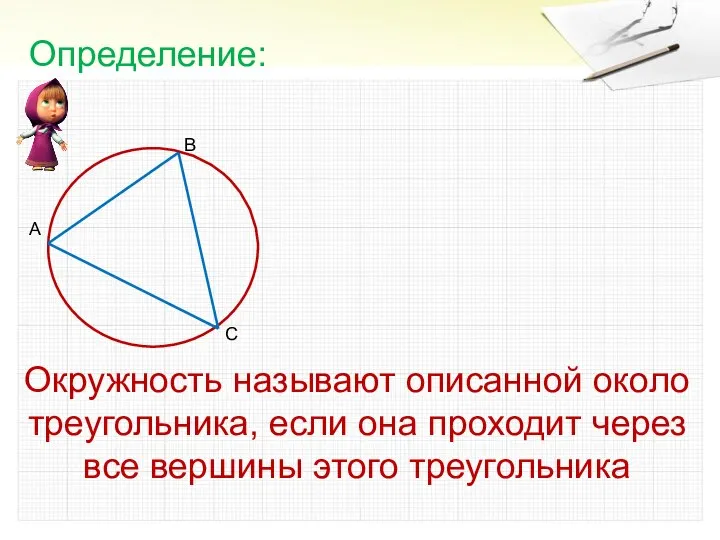
Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника
Определение:

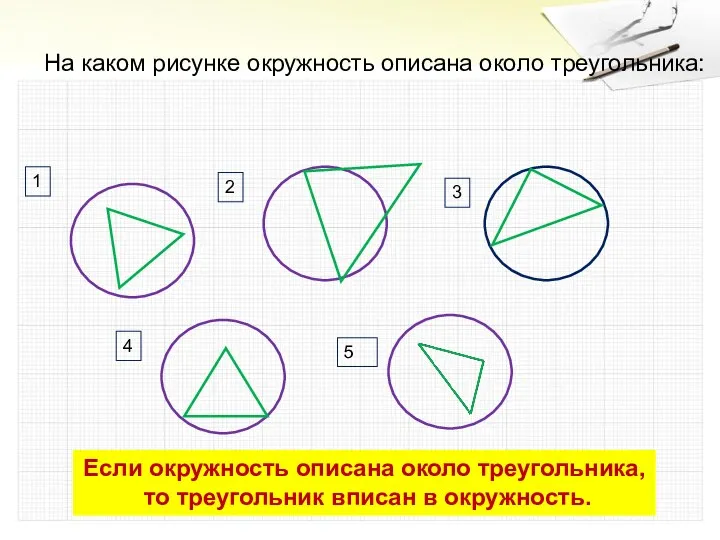
На каком рисунке окружность описана около треугольника:
1
2
3
4
5
Если окружность описана около треугольника,
то треугольник вписан в окружность.

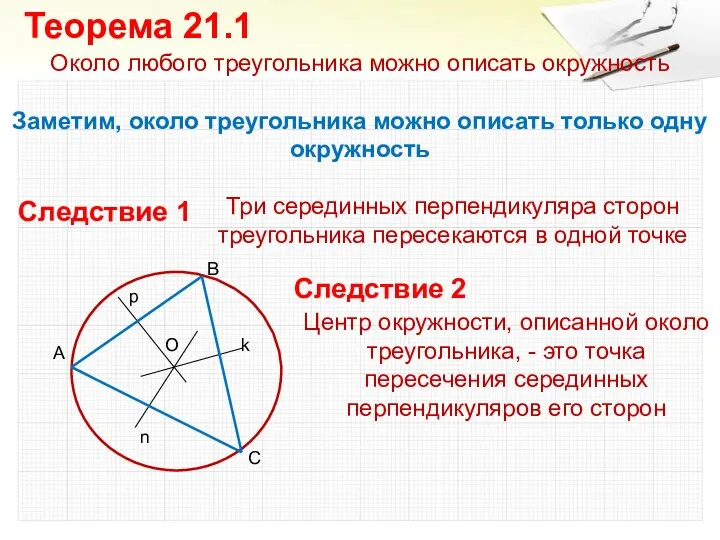
Около любого треугольника можно описать окружность
Заметим, около треугольника можно описать только одну окружность
Теорема 21.1
Три серединных перпендикуляра сторон треугольника пересекаются в одной точке
Следствие 1
Следствие 2
Центр окружности, описанной около треугольника, - это точка пересечения серединных перпендикуляров его сторон

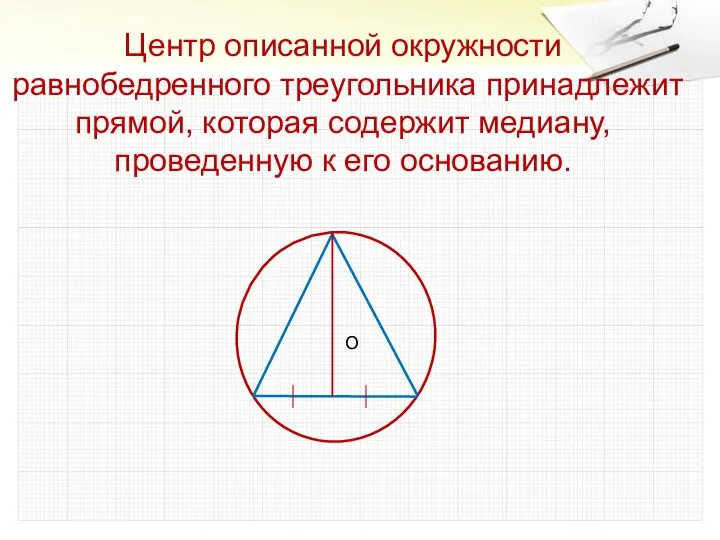
Центр описанной окружности равнобедренного треугольника принадлежит прямой, которая содержит медиану, проведенную к его основанию.
О

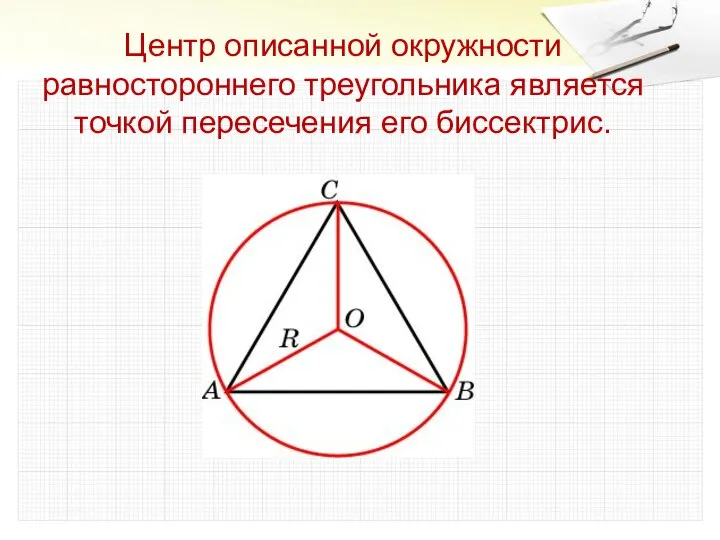
Центр описанной окружности равностороннего треугольника является точкой пересечения его биссектрис.