Содержание
- 2. Основы математической статистики Большой раздел современной матема-тической статистики — статистический последовательный анализ, фундаментальный вклад в создание
- 3. Выборочный метод Выборочный метод заключается в том, что из общей совокупности объектов, называемых генеральной совокупностью, извлекают
- 4. Пример использования «выборочного метода» - расчёт потерь Пример. Как правило, после расчёта потерь электроэнергии в сетях
- 5. Доверительные интервалы Доверительный интервал – термин, используемый в математической статистике при интервальной оценке статистических параметров, более
- 6. Доверительные интервалы
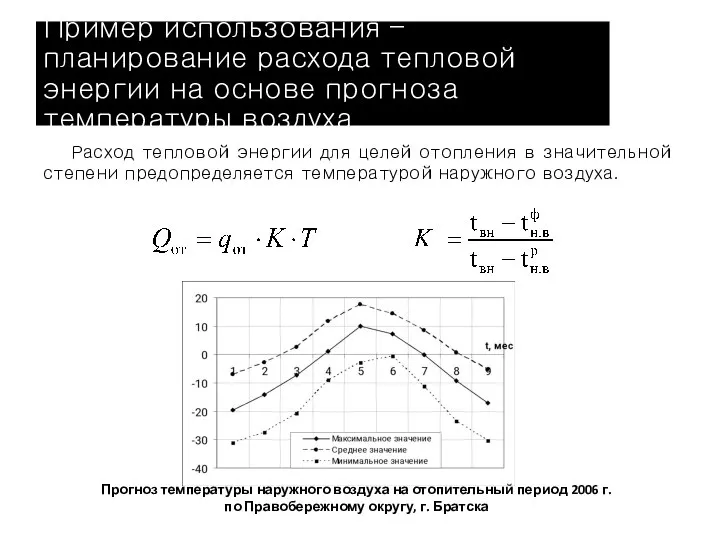
- 7. Пример использования – планирование расхода тепловой энергии на основе прогноза температуры воздуха Расход тепловой энергии для
- 8. Проверка статистических гипотез Проверка статистических гипотез является содержанием одного из обширных классов задач математической статистики. Статистическая
- 9. Проверка статистических гипотез Метод проверки статистической гипотезы состоит в следующем. Производится выборка, на основе которой вычисляется
- 10. Проверка статистических гипотез Критерии значимости - проверка гипотез о нормальности выборки Критерий Шапира-Уилка Критерий хи-квадрат Пирсона
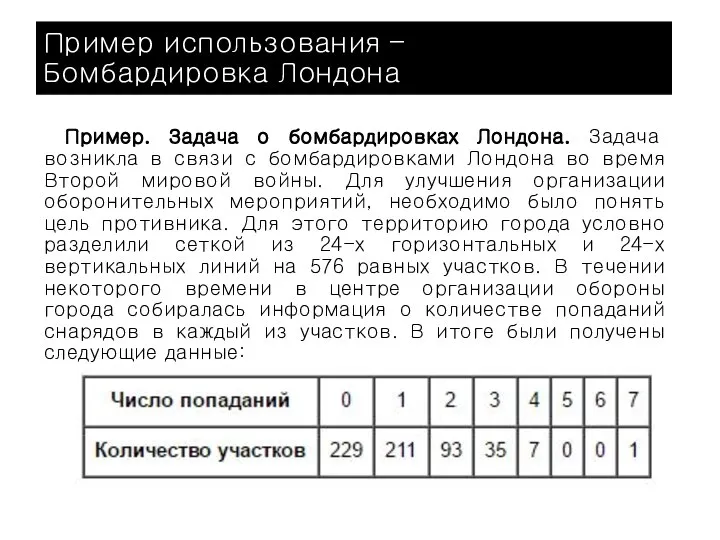
- 11. Пример использования – Бомбардировка Лондона Пример. Задача о бомбардировках Лондона. Задача возникла в связи с бомбардировками
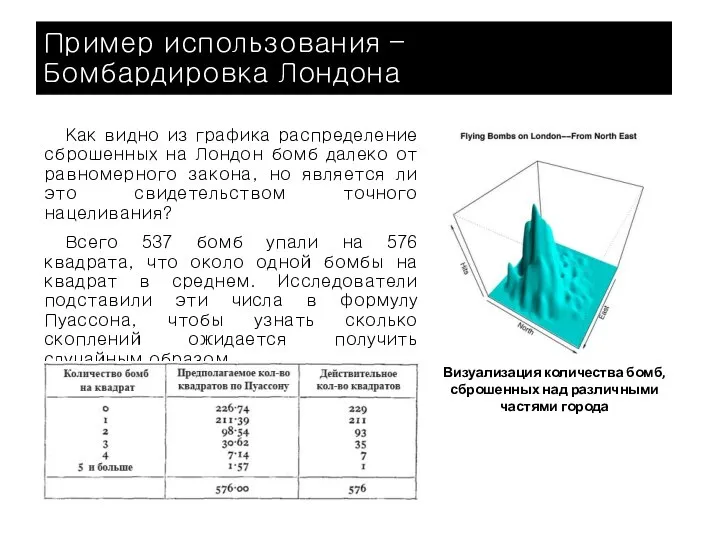
- 12. Пример использования – Бомбардировка Лондона Как видно из графика распределение сброшенных на Лондон бомб далеко от
- 13. Гипотеза H0: стрельба случайна (нет "целевых" участков). Закон редких событий (распределение Пуассона) Тогда при уровне значимости
- 14. Отсев грубых ошибок Исходные данные, получаемые в результате экспериментов, в силу разных причин, могут содержать грубые
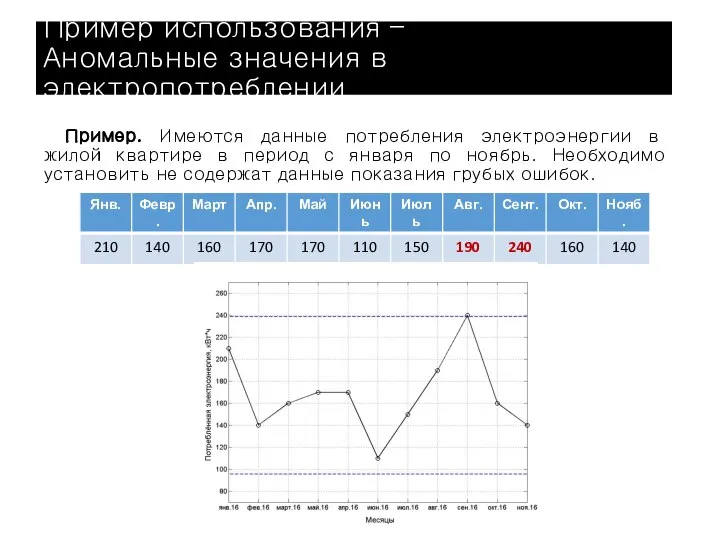
- 15. Пример. Имеются данные потребления электроэнергии в жилой квартире в период с января по ноябрь. Необходимо установить
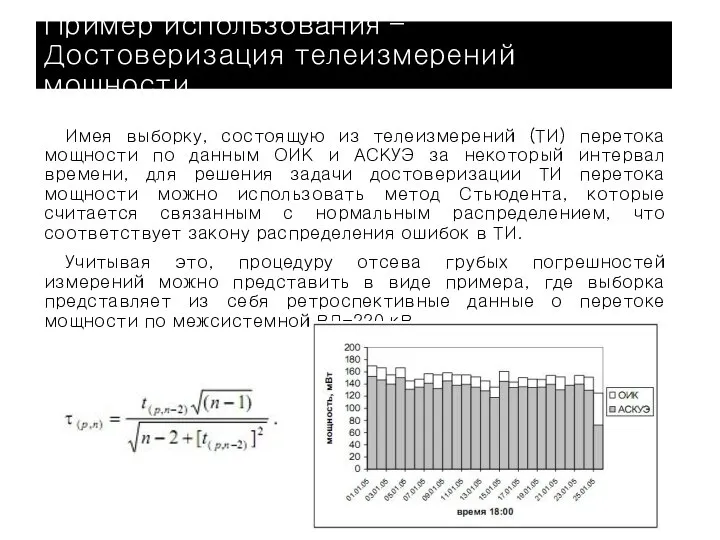
- 16. Пример использования – Достоверизация телеизмерений мощности Имея выборку, состоящую из телеизмерений (ТИ) перетока мощности по данным
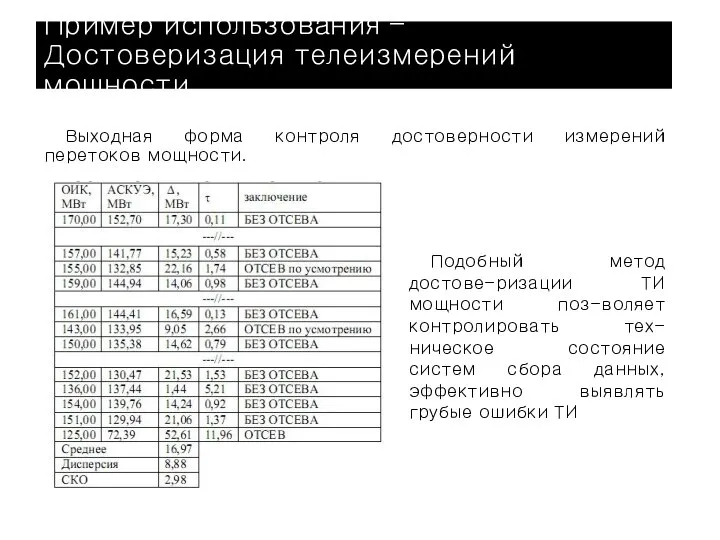
- 17. Пример использования – Достоверизация телеизмерений мощности Выходная форма контроля достоверности измерений перетоков мощности. Подобный метод достове-ризации
- 18. Регрессионный анализ Величины, характеризующие различные свойства объектов, могут быть независимыми или взаимосвязанными. Различают два вида взаимосвязи:
- 19. Регрессионный анализ Термин "регрессия" был введён Фрэнсисом Гальтоном в конце 19-го века. Гальтон обнаружил, что дети
- 20. Регрессионный анализ Регрессия — зависимость математического ожидания (например, среднего значения) случайной величины от одной или нескольких
- 21. Регрессионный анализ
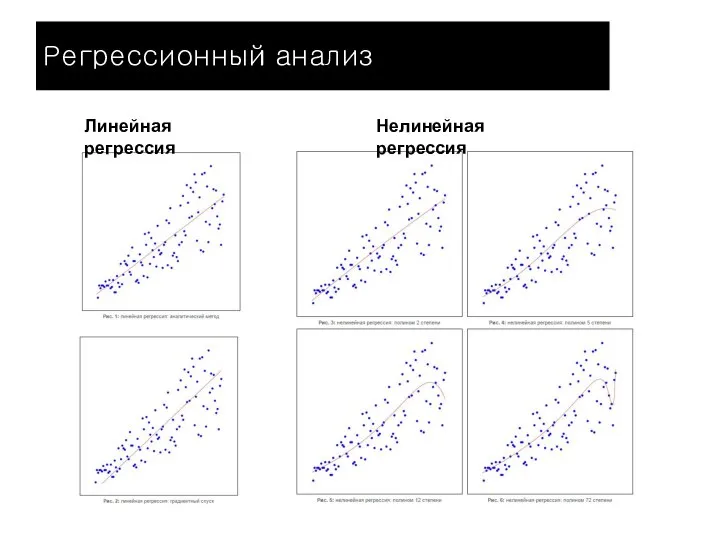
- 22. Регрессионный анализ Линейная регрессия Нелинейная регрессия
- 23. Регрессионный анализ Решение задачи регрессионного анализа целесообразно разбить на несколько этапов: предварительная обработка данных; выбор вида
- 24. Регрессионный анализ Уравнение регрессии в регрессионном анализе следует трактовать как векторное, ибо речь идет о матрице
- 25. Регрессионный анализ – метод наименьших квадратов
- 26. Регрессионный анализ – метод наименьших квадратов В основе МНК лежат следующие положения: значения величин ошибок и
- 27. Регрессионный анализ Качество полученного уравнения регрессии оценивают по степени близости между результатами наблюдений за показателем и
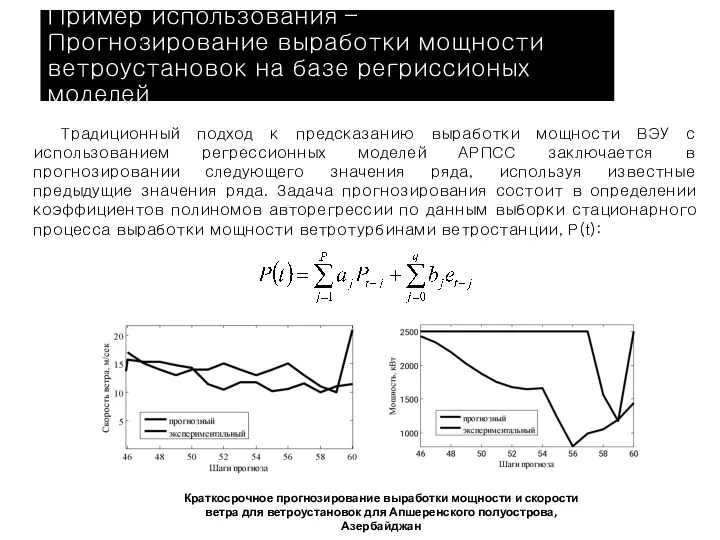
- 28. Традиционный подход к предсказанию выработки мощности ВЭУ с использованием регрессионных моделей АРПСС заключается в прогнозировании следующего
- 29. Пример использования – Моделирование распределение температуры оборудования от параметров работы электровозов при их движении Тепловой нагрев
- 30. Пример использования – Моделирование распределение температуры оборудования от параметров работы электровозов при их движении Установлено, что
- 31. Корреляционный анализ Для управления сложными системами, на которые воздействует множество факторов, необходимо иметь представление о факторах,
- 32. Корреляционный анализ Употребляется в науке с конца XYIII века. Его ввел французский палеонтолог Жорж Кювье, основавший
- 33. Корреляционный анализ Корреляция - это статистическая зависимость между случайными величинами, не имеющая строго функционального характера, при
- 34. Корреляционный анализ – основная идея Идея сопоставления колебаний значений признака относительно друг друга Если численные значения
- 35. Корреляционный связь Характеризует сложный механизм взаимодействия двух или нескольких признаков При котором при изменении одного признака
- 36. Коэффициент корреляции Пирсона Предполагает, что: обе переменные распределены нормально связь линейна Коэффициент корреляции Пирсона основан на
- 37. Корреляционный анализ при r > 0,85 (при этом варьирование признаков взаимосвязано приблизительно на 75% и более)
- 38. Коэффициент Спирмена Не предполагает, что данные распределены каким-то особым образом Вместо исходных значений использует их ранги
- 39. Оценка значимости корреляции Оценка коэффициента корреляции, вычисленная по ограниченной выборке, практически всегда отличается от нуля. Но
- 40. Оценка значимости корреляции Для проверки гипотезы о значимости коэффициента корреляции используется критерий Стьюдента в виде: В
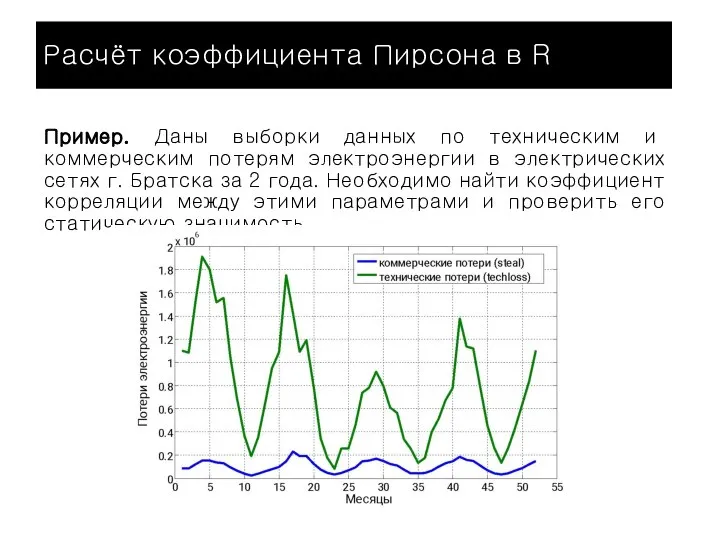
- 41. Расчёт коэффициента Пирсона в R Пример. Даны выборки данных по техническим и коммерческим потерям электроэнергии в
- 42. Расчёт коэффициента Пирсона в R #корреляционный анализ Pearson's product-moment correlation data: loss$techloss and loss$steal t =
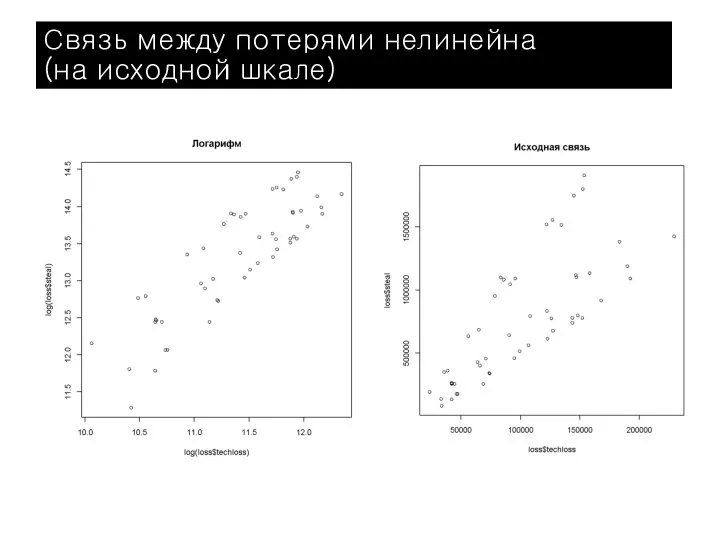
- 43. Связь между потерями нелинейна (на исходной шкале)
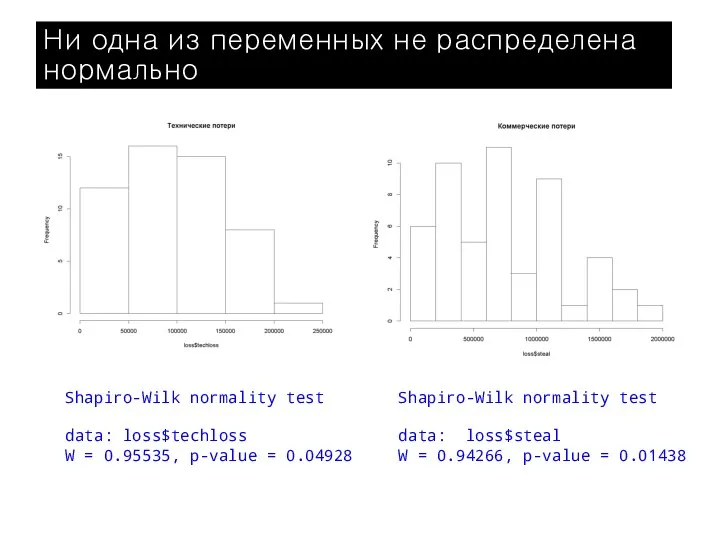
- 44. Ни одна из переменных не распределена нормально Shapiro-Wilk normality test data: loss$techloss W = 0.95535, p-value
- 46. Скачать презентацию
































 Неравенства. Практическая работа №3
Неравенства. Практическая работа №3 Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Презентация Понономарев
Презентация Понономарев Задачки от жителей Солнечного города. 1 класс
Задачки от жителей Солнечного города. 1 класс Простые и составные числа
Простые и составные числа Умножение обыкновенных дробей
Умножение обыкновенных дробей Решение треугольников
Решение треугольников Кенгуру – математика для всех
Кенгуру – математика для всех Основные законы распределения непрерывных случайных величин
Основные законы распределения непрерывных случайных величин Перпендикулярные прямые
Перпендикулярные прямые Справочник по геометрии
Справочник по геометрии Геометрический смысл производной. Производная и её геометрический смысл
Геометрический смысл производной. Производная и её геометрический смысл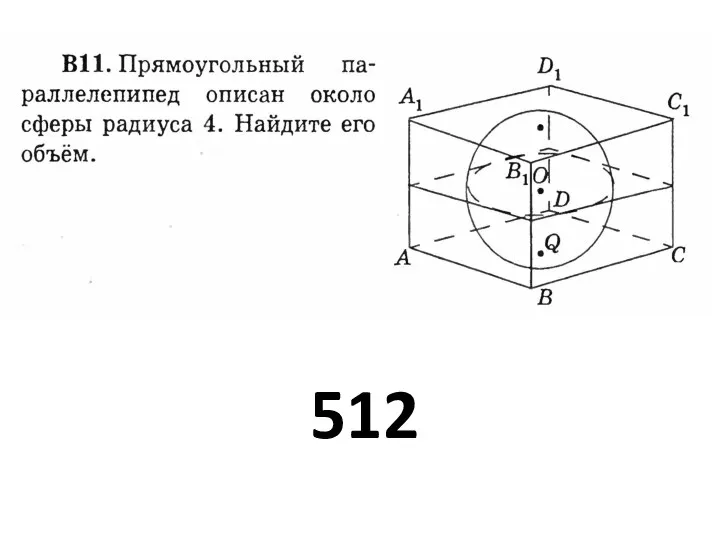 Решение задач по геометрии
Решение задач по геометрии Критические точки функции
Критические точки функции Рациональные числа 6 класс - Презентация по математике_
Рациональные числа 6 класс - Презентация по математике_ Регрессионный анализ
Регрессионный анализ Призма. Площадь полной поверхности прямой призмы
Призма. Площадь полной поверхности прямой призмы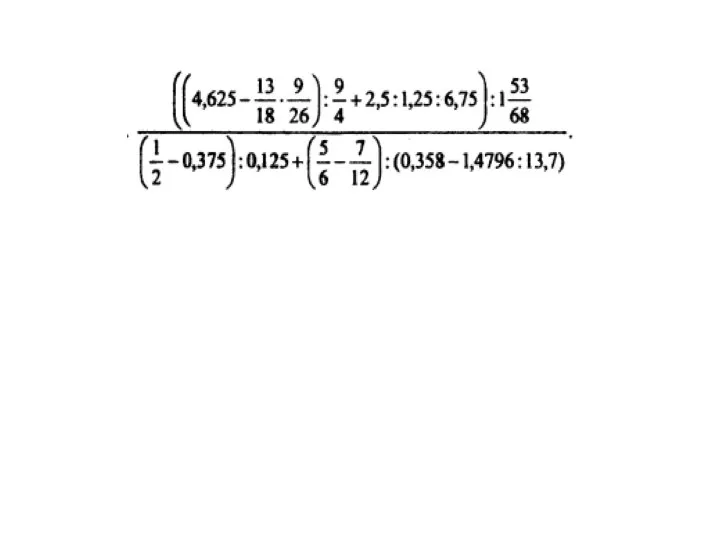 Тождественное преобразование алгебраических выражений. Продолжение
Тождественное преобразование алгебраических выражений. Продолжение Золотое сечение - красота и гармония в математических расчетах
Золотое сечение - красота и гармония в математических расчетах Презентация на тему ОТЫСКАНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ
Презентация на тему ОТЫСКАНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ  Презентация на тему ИСТОРИЯ ВОЗНИКНОВЕНИЯ ЧАСОВ
Презентация на тему ИСТОРИЯ ВОЗНИКНОВЕНИЯ ЧАСОВ  Математика в медицине
Математика в медицине Пропорция
Пропорция Интеграл. Первообразная
Интеграл. Первообразная Единицы объёма. Задания
Единицы объёма. Задания Среднее арифметическое. Задания
Среднее арифметическое. Задания Показательные уравнения, сводящиеся к квадратным
Показательные уравнения, сводящиеся к квадратным Математика. Вычитание
Математика. Вычитание