Содержание
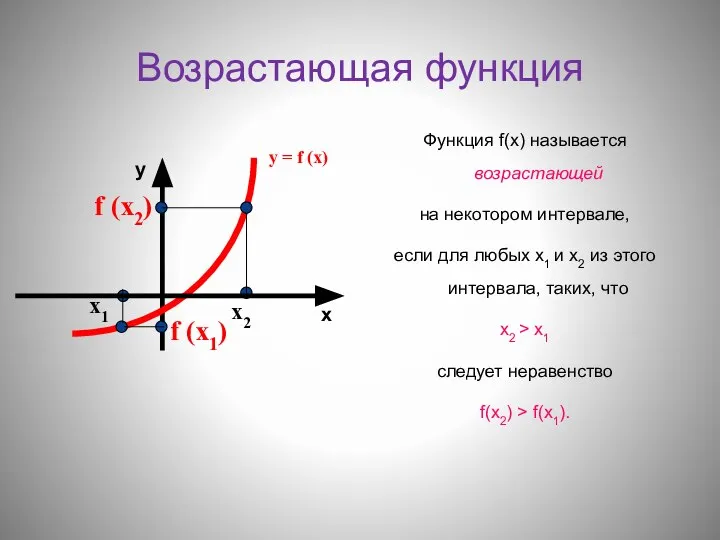
- 2. Возрастающая функция Функция f(х) называется возрастающей на некотором интервале, если для любых х1 и х2 из
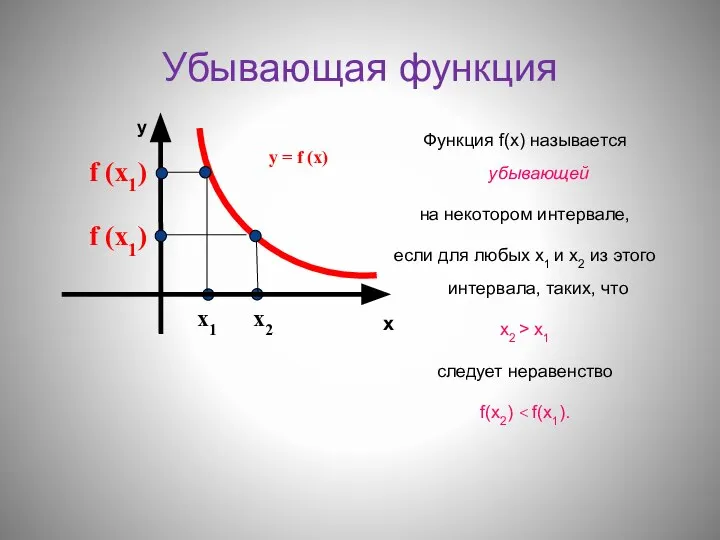
- 3. Убывающая функция Функция f(х) называется убывающей на некотором интервале, если для любых х1 и х2 из
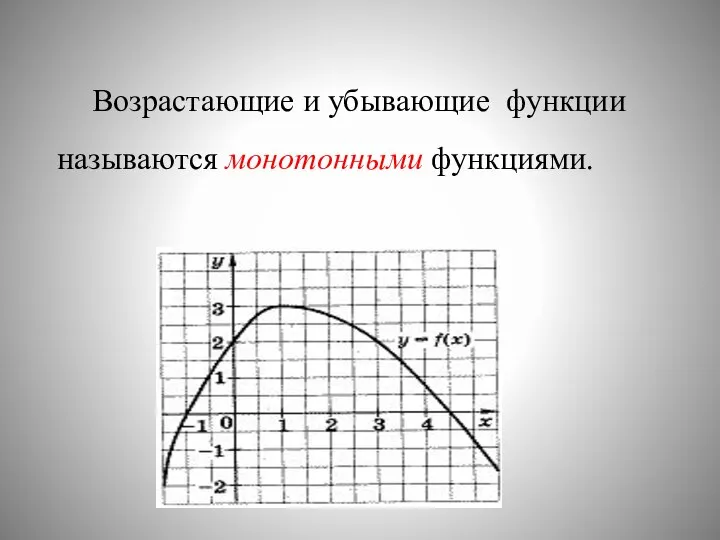
- 4. Возрастающие и убывающие функции называются монотонными функциями.
- 5. Способы исследования функций на монотонность Способ 1. По определению возрастающей (убывающей) функции. Способ 2. По графику
- 6. Пример №1. Исследуйте функцию f(x)= 1/х на По определению: монотонность. Решение. Область определения: D(f) : х
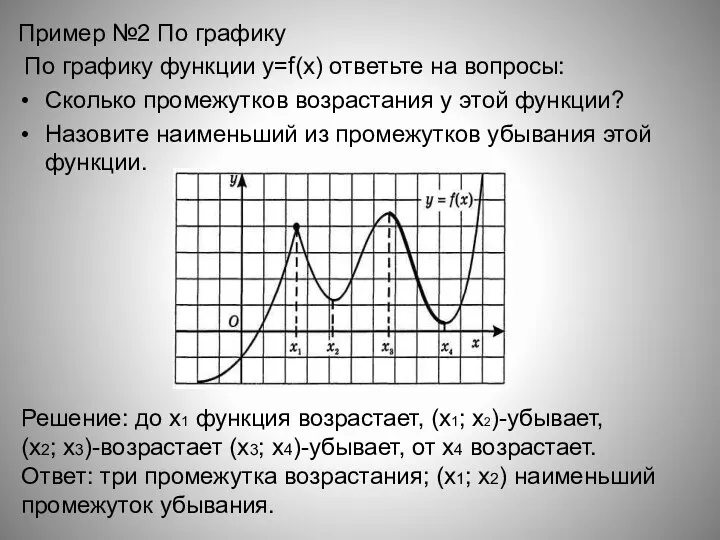
- 7. Пример №2 По графику По графику функции y=f(x) ответьте на вопросы: Сколько промежутков возрастания у этой
- 8. Наши цели 1. Найти связь между производной и свойством монотонности функции. 2. Создать алгоритм поиска промежутков
- 9. Тема урока: «Возрастание и убывание функции»
- 11. Гипотеза Если f/(x) > 0 на некотором интервале, то функция возрастает на этом интервале. Если f/(x)
- 12. Достаточный признак возрастания(убывания) функции
- 13. Алгоритм 1. Указать область определения функции. 2. Найти производную функции. 3. Определить промежутки, в которых f/(x)
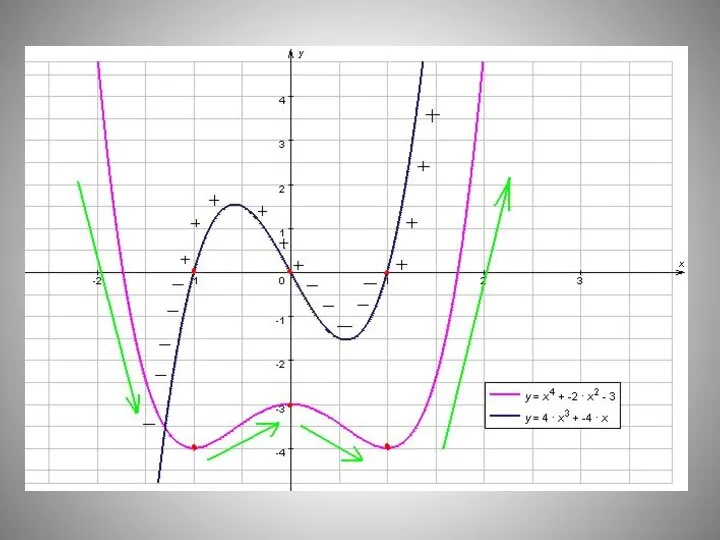
- 14. Образец решения по алгоритму f(х) = х4 - 2х2 , 1. D(f) = R 2. f/(x)
- 15. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её производной. Укажите количество промежутков возрастания
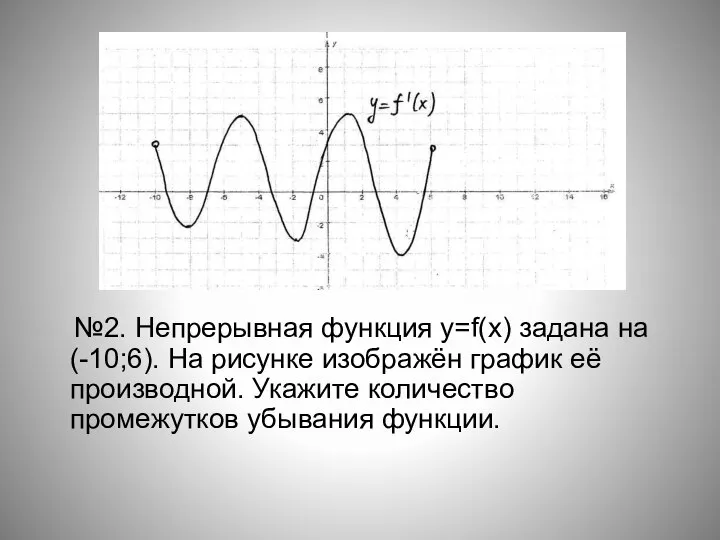
- 16. №2. Непрерывная функция y=f(x) задана на (-10;6). На рисунке изображён график её производной. Укажите количество промежутков
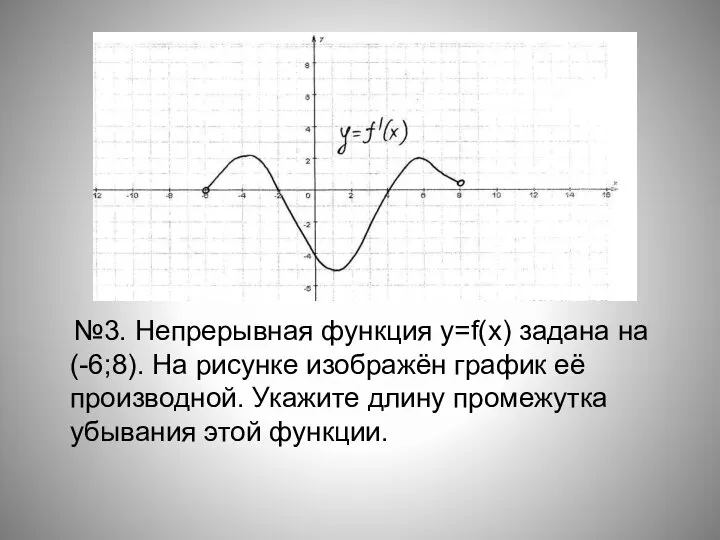
- 17. №3. Непрерывная функция y=f(x) задана на (-6;8). На рисунке изображён график её производной. Укажите длину промежутка
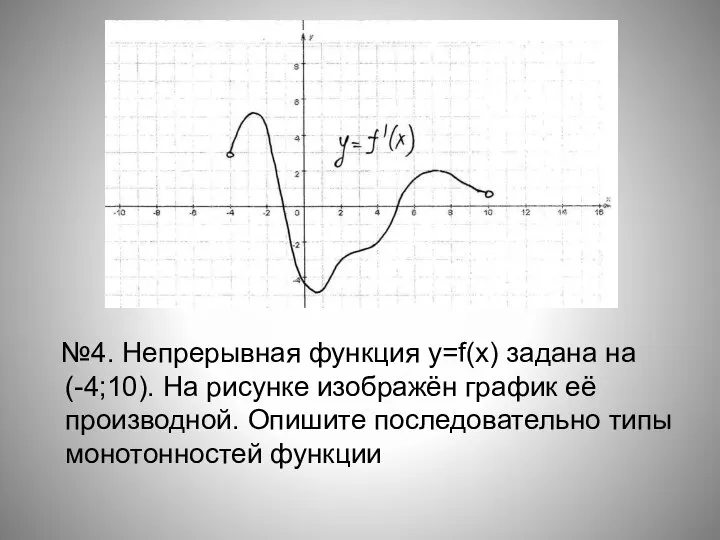
- 18. №4. Непрерывная функция y=f(x) задана на (-4;10). На рисунке изображён график её производной. Опишите последовательно типы
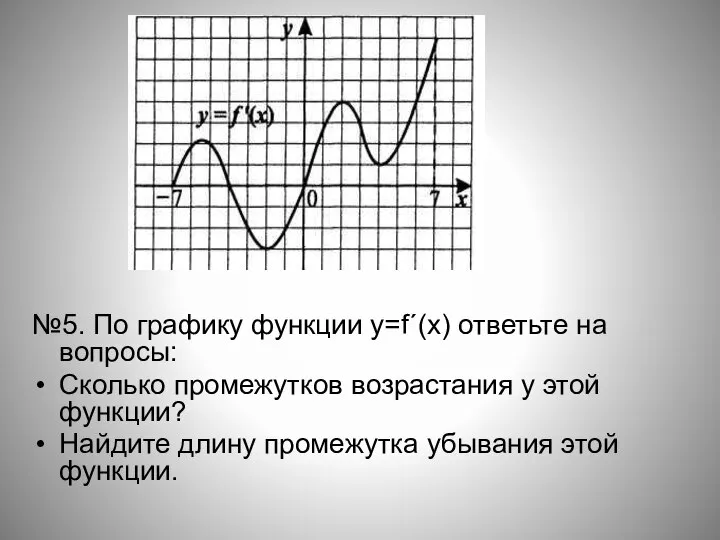
- 19. №5. По графику функции y=f´(x) ответьте на вопросы: Сколько промежутков возрастания у этой функции? Найдите длину
- 21. Скачать презентацию








![Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её производной.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/937722/slide-14.jpg)
 Геометрическое шоу Десять пятерок
Геометрическое шоу Десять пятерок Sie hat Geburtstag am fünften August. Er kommt am einunddreißigsten Juli
Sie hat Geburtstag am fünften August. Er kommt am einunddreißigsten Juli Решение планиметрических задач
Решение планиметрических задач Презентация по математике "УУД, которые формируются у ученика в процессе изучения математики в 4 классе" -
Презентация по математике "УУД, которые формируются у ученика в процессе изучения математики в 4 классе" -  Деление взаимно обратных чисел
Деление взаимно обратных чисел Презентация на тему Геометрические фигуры (2 класс)
Презентация на тему Геометрические фигуры (2 класс)  Пирамида. Элементы пирамиды
Пирамида. Элементы пирамиды Весёлые клоуны. Игра по математике для 1 класса
Весёлые клоуны. Игра по математике для 1 класса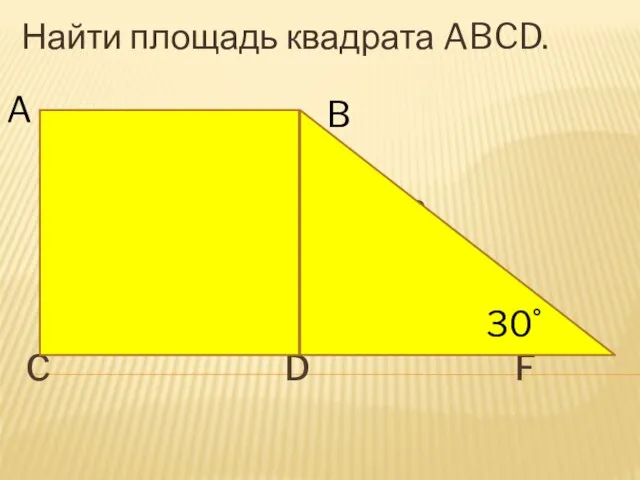 Решение задач. Площадь квадрата
Решение задач. Площадь квадрата Приложения производной
Приложения производной Презентация на тему Состав числа 5
Презентация на тему Состав числа 5  Построение сечений тетраэдра
Построение сечений тетраэдра Параллельность в пространстве
Параллельность в пространстве Наука Метрология
Наука Метрология Угол. Луч
Угол. Луч Презентация на тему Противоположные числа (6 класс)
Презентация на тему Противоположные числа (6 класс)  Логические и традиционные головоломки
Логические и традиционные головоломки Умножение натуральных чисел
Умножение натуральных чисел Тренажер. Примеры
Тренажер. Примеры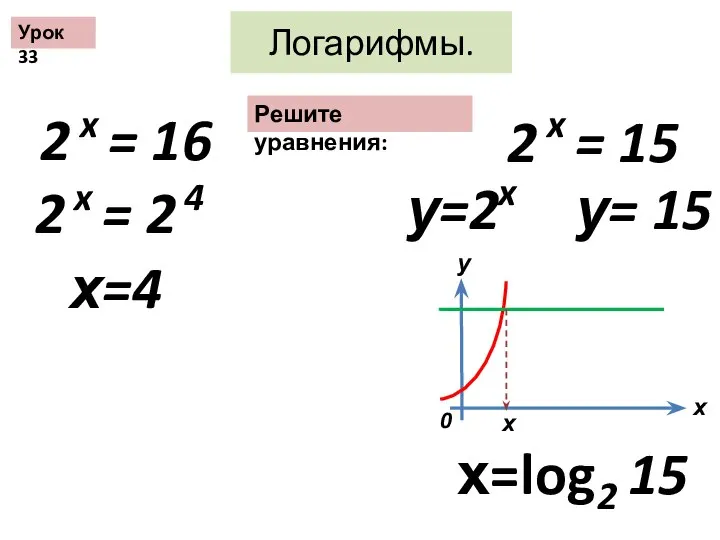 Логарифмы
Логарифмы Потенцирование логарифмических выражений
Потенцирование логарифмических выражений Презентация на тему Разложение многочлена на множители 7 класс
Презентация на тему Разложение многочлена на множители 7 класс  Урок по теме Многочлен и его стандартный вид
Урок по теме Многочлен и его стандартный вид Презентация на тему Решение задач на построение сечений многогранников
Презентация на тему Решение задач на построение сечений многогранников  Среднее арифметическое
Среднее арифметическое Элементы векторной алгебры
Элементы векторной алгебры ТРАПЕЦІЯ
ТРАПЕЦІЯ Игра 7
Игра 7