Слайд 2Предисловие
История возникновения формулы производной начинается ещё в 15 веке. Великий итальянский математик

Тартальи, рассматривая и развивая вопрос – на сколько зависит дальность полёта снаряда от наклона орудия – применяет её в своих трудах.
Слайд 3Производная - это предел отношения приращения функции к приращению аргумента, если приращение

аргумента стремится к нулю.
Слайд 4Производная находит своё применение в ряде следующих наук:
☺ Биология
☺ Химия
☺ Экономика
☺ География
☺ Физика

Слайд 5Биология
Биология — это наука о живых существах и их взаимодействии со средой

обитания.
Важный принцип биологии - популяции, которые находятся в теоретическом значении только благодаря производным. Вычисление скорости роста, пребывания популяций и средней продолжительности их жизни происходят благодаря производным.
Слайд 6Химия
Химия – это наука о веществах и о химических превращениях веществ.
Производная нашла

широкое применение в химии для построения математических моделей химических реакций и последующего описания их свойств. Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности.
Слайд 7Экономика
Экономика - это наука о деятельности людей по поводу производства и обмена

продуктов.
С помощью производной в экономике можно рассчитать наивысшую производительность труда, максимальную прибыль, максимальный выпуск продукции и минимальные издержки производства
Слайд 8География
География - это наука, которая изучает поверхность Земли, её природные условия, распределение

на ней природных объектов
В географии производная используется в расчётах некоторых значений в сейсмографии, особенностях электромагнитного поля земли, радиоактивности ядерно-геофизических показателей и численности населения на территории в момент времени в t
Слайд 9Физика
Физика - это наука о наиболее общих законах природы, о материи, её

структуре, движении и правилах трансформации
Производная в физике применяется в основном для вычисления наибольших или наименьших значений каких-либо величин, например, скорости, ускорения, силы тока, теплоёмкости, угловая скорость








 Презентация на тему Аксиома параллельных прямых
Презентация на тему Аксиома параллельных прямых  Презентация на тему ЗАДАЧИ НА ДРОБИ
Презентация на тему ЗАДАЧИ НА ДРОБИ 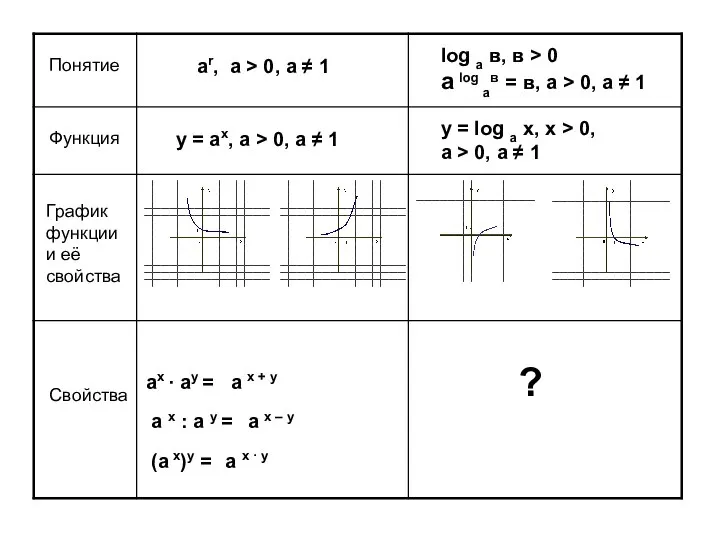 Свойства логарифмов
Свойства логарифмов Устный счёт. Состав числа 6. 1 класс
Устный счёт. Состав числа 6. 1 класс Sluchaynye_velichiny_14_sen
Sluchaynye_velichiny_14_sen Действительный анализ
Действительный анализ Математика. Задания по учебнику
Математика. Задания по учебнику Математическая викторина
Математическая викторина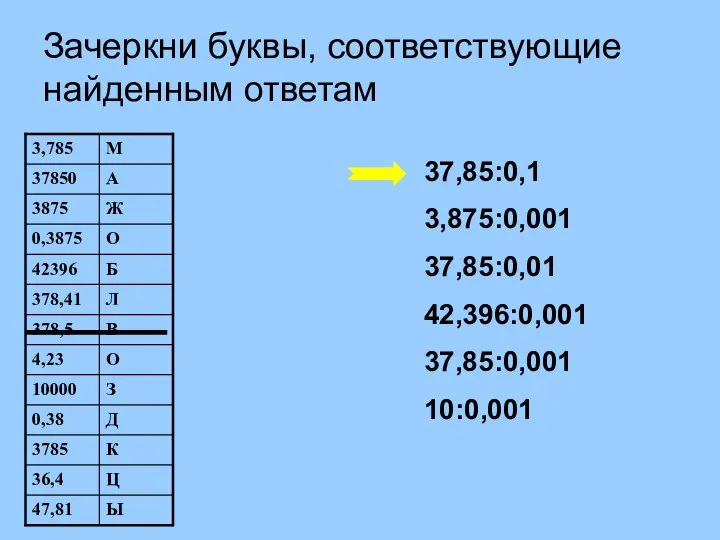 Устная работа (1). Зачеркни буквы, соответствующие найденным ответам
Устная работа (1). Зачеркни буквы, соответствующие найденным ответам Комплексные числа. Понятие мнимой единицы. Алгебраическая форма комплексного числа. Последовательности
Комплексные числа. Понятие мнимой единицы. Алгебраическая форма комплексного числа. Последовательности Задачи на готовых чертежах: Перпендикулярность плоскостей
Задачи на готовых чертежах: Перпендикулярность плоскостей Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Разминка. Подготовка к ГИА
Разминка. Подготовка к ГИА Площадь параллелограмма
Площадь параллелограмма Сравнение чисел
Сравнение чисел Комбинаторика
Комбинаторика Презентация на тему Линейная функция 6 класс
Презентация на тему Линейная функция 6 класс  Задачи на кратное сравнение
Задачи на кратное сравнение Градусная мера дуги окружности. Теорема о вписанном угле
Градусная мера дуги окружности. Теорема о вписанном угле Геометриялық фигуралар
Геометриялық фигуралар Презентация по математике "Табличное умножение и деление" -
Презентация по математике "Табличное умножение и деление" -  Квадратные корни. 8 класс
Квадратные корни. 8 класс Психолого – педагогические основы организации математического развития младших школьников
Психолого – педагогические основы организации математического развития младших школьников Базіс лінейнай прасторы. Каардынаты
Базіс лінейнай прасторы. Каардынаты Перпендикулярность плоскостей. 10 класс
Перпендикулярность плоскостей. 10 класс Функции и их графики. 9 класс
Функции и их графики. 9 класс Задачи на нахождение неизвестного
Задачи на нахождение неизвестного