Содержание
- 2. Основные свойства неопределенного интеграла Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от
- 3. Непосредственное интегрирование Ex 1: (a – b)3 = a3 – 3a2b + 3ab2 - b3 Ex
- 4. Ex 1: ∫(x – 3)3 dx = Вывод 1: Ex 2: ∫(3x + 7)25 = Вывод
- 6. Скачать презентацию



 Виды графов
Виды графов Тройные интегралы в цилиндрических координатах
Тройные интегралы в цилиндрических координатах Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе
Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе Китайская математика
Китайская математика Дополнительные задачи. 7 класс
Дополнительные задачи. 7 класс Множители и произведение
Множители и произведение Математика учит точности мысли
Математика учит точности мысли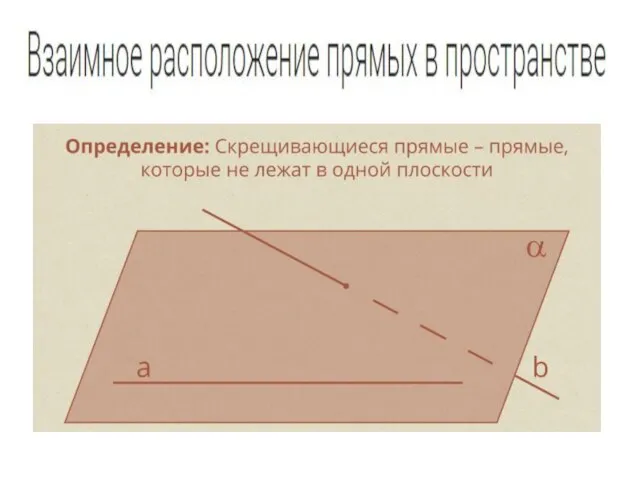 Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве Подбираем наибольшее произведение
Подбираем наибольшее произведение В мире геометрии
В мире геометрии Элементы комбинаторики
Элементы комбинаторики Простейшие задачи в координатах
Простейшие задачи в координатах Цифровые устройства. Логические функции и их минимизация
Цифровые устройства. Логические функции и их минимизация Линейные пространства и подпространства
Линейные пространства и подпространства Простейшие задачи в координатах
Простейшие задачи в координатах Задачи на проценты
Задачи на проценты Площадь треугольника
Площадь треугольника Презентация на тему История теоремы Пифагора
Презентация на тему История теоремы Пифагора  Частные производные второго порядка
Частные производные второго порядка Проценты в медицине
Проценты в медицине Сложение с переходом через десяток
Сложение с переходом через десяток Сходимость последовательности СВ
Сходимость последовательности СВ Квадратные уравнения
Квадратные уравнения Предел последовательности. Практическая работа № 24
Предел последовательности. Практическая работа № 24 Моделирование в технике
Моделирование в технике Пропорциональность отрезков хорд и секущих окружности
Пропорциональность отрезков хорд и секущих окружности Элементы комбинаторики
Элементы комбинаторики Закон больших чисел и предельные теоремы
Закон больших чисел и предельные теоремы