Преобразование графиков тригонометрических функций

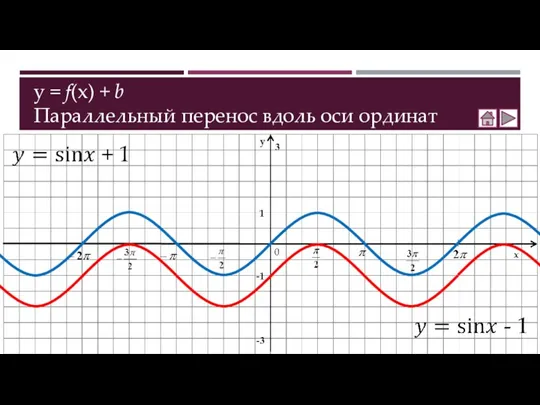
y = f(x) + b
Параллельный перенос вдоль оси ординат
3
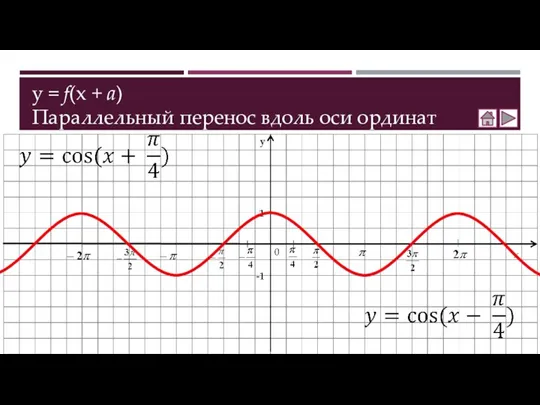
-3

y = f(x + a)
Параллельный перенос вдоль оси ординат

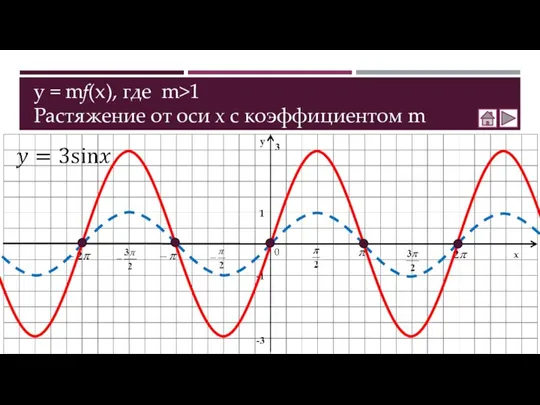
y = mf(x), где m>1
Растяжение от оси х с коэффициентом m
3
-3

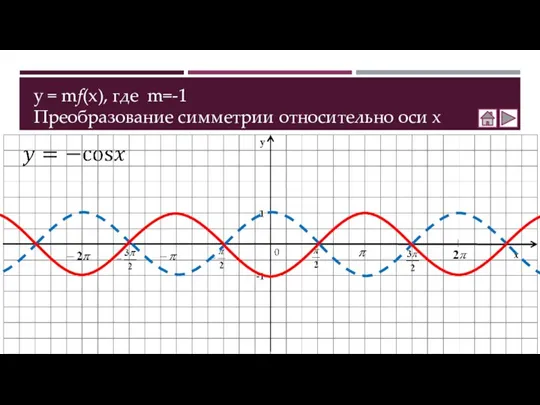
y = mf(x), где m=-1
Преобразование симметрии относительно оси х

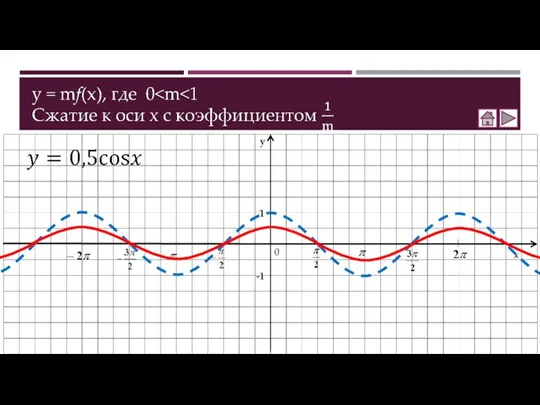
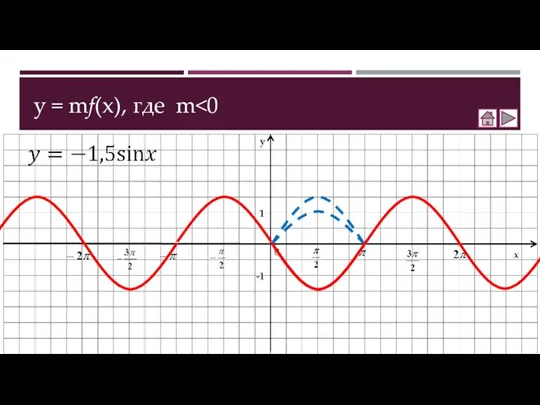
y = mf(x), где m<0

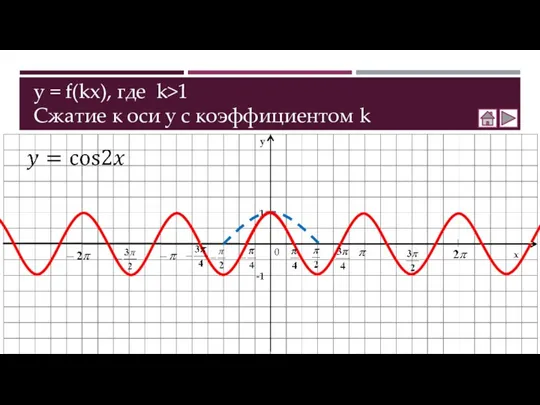
y = f(kx), где k>1
Сжатие к оси у с коэффициентом k