Слайд 2
Математику нельзя изучать, наблюдая, как это делает сосед.
А. Нивен

Слайд 3Свойства сложения, вычитания, умножения и деления полезны тем, что позволяют преобразовывать суммы

и
произведения в удобные выражения
для вычислений.
Научимся, как можно с помощью этих свойств упрощать выражения.
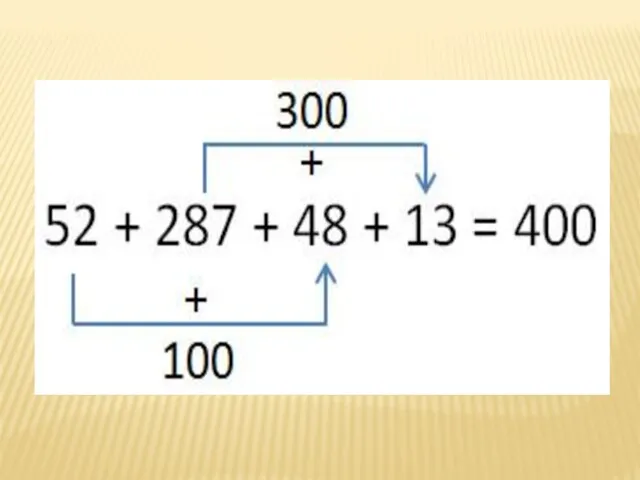
Слайд 4Вычислим сумму:
52 + 287 + 48 + 13 =
В этом выражении

есть числа, при сложении которых получаются "круглые" числа. Заметив это, легко провести вычисления устно. Воспользуемся переместительным законом сложения:
а + в = в + а
Слайд 6 Также для упрощения вычисления произведений можно использовать переместительный закон умножения:
а ·в

= в · а
7 • 2 • 9 • 5 = (2 • 5) • (7 • 9) = 10 • 63 = 630
Слайд 7Сочетательные (а·в)·с = а·(в·с)
и переместительные а ·в = в · а
свойства умножения

используются и при
упрощении буквенных выражений:
6 • a • 2 = 6 • 2 • a = 12a
2 • a • 4 • b = 2 • 4 • a • b = 8ab
5b + 8b = (5 + 8) • b = 13b
14y - 12y = (14 - 12) • y = 2y
Слайд 8Распределительный закон умножения
часто применяется для упрощения
вычислений.

Слайд 9Применяя распределительное свойство умножения
относительно сложения или вычитания к выражению
(a+ b) •

с и (a - b) • c, мы получаем выражение, не
содержащее скобки. В этом случае говорят, что мы
раскрыли (опустили) скобки. Для применения свойств
не имеет значения, где записан множитель "c" – перед
скобками или после.
Раскроем скобки в выражениях:
2(t + 8) = 2t + 16
(3b - 5)4 = 4 • 3b - 4 • 5 = 12b - 20
Слайд 10
ЗАПОМНИТЕ!!!
Если перед буквой не записано число, то
подразумевается, что перед буквой стоит числовой
множитель

1.
t + 4t = (1 + 4)t = 5t
Вынесение общего множителя за скобки
Поменяем местами правую и левую часть равенства:
(a + b)с = ac + bc
Получим:
ac + bc = (a + b)с
В таких случаях говорят, что из "ac + bc" вынесен общий
множитель "с" за скобки.
Слайд 11Примеры вынесения общего множителя за
скобки.
73 • 8 + 7 • 8 =

(73 + 7) • 8 = 80 • 8 = 640
7x - x - 6 = (7 - 1)x - 6 = 6x - 6 = 6(x - 1)
Слайд 13х· 9· 4· у
3· в· 12
с· 18· d· 3
36· в
36· х· у
54·
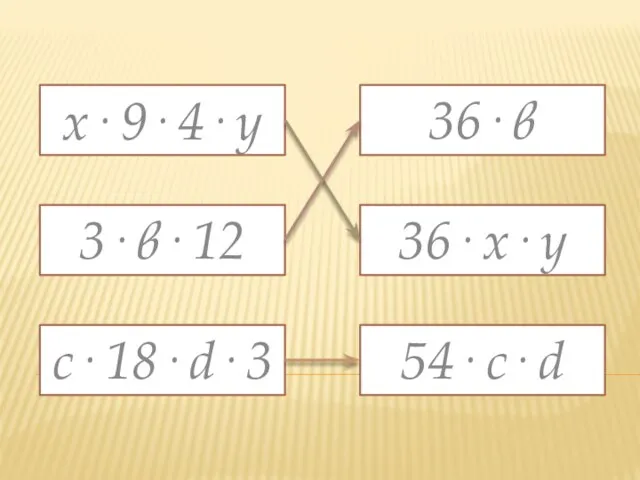
с· d
Слайд 14х· 4· 8· у
12y – 3y
5x + 6x +8y -·2y
9y
11в + 3
32xy
18в












 Презентация на тему Связь между слагаемыми и суммой
Презентация на тему Связь между слагаемыми и суммой  Экстремумы (1)
Экстремумы (1) Урок 23
Урок 23 Перпендикулярные прямые
Перпендикулярные прямые Своя игра. Треугольники
Своя игра. Треугольники Множество значений тригонометрических функций
Множество значений тригонометрических функций Презентация на тему Параллельность прямых и плоскостей (10 класс)
Презентация на тему Параллельность прямых и плоскостей (10 класс)  Презентация на тему Уравнение х2=а (8 класс)
Презентация на тему Уравнение х2=а (8 класс)  Арккосинус а. Решение уравнений
Арккосинус а. Решение уравнений Смежные и вертикальные углы
Смежные и вертикальные углы Вписанные окружности (решение задач)
Вписанные окружности (решение задач) Решение планиметрических задач на стереометрических чертежах
Решение планиметрических задач на стереометрических чертежах Параллельные прямые, перпендикулярные к плоскости
Параллельные прямые, перпендикулярные к плоскости Линейная функция
Линейная функция Многоугольники
Многоугольники Виды треугольников
Виды треугольников Введение в стереометрию
Введение в стереометрию Решение иррациональных уравнений
Решение иррациональных уравнений Анализ ошибок. Параллелепипеды. 10 класс
Анализ ошибок. Параллелепипеды. 10 класс Решение задач ЕГЭ по тригонометрии
Решение задач ЕГЭ по тригонометрии Числа 1 – 5 закрепление
Числа 1 – 5 закрепление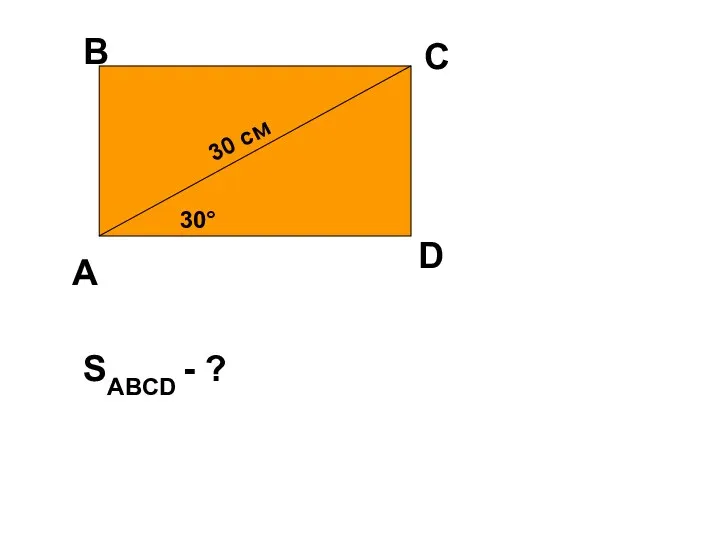 Параметры четырехугольника
Параметры четырехугольника Случаи вычитания
Случаи вычитания Пивкин ИКС-34 (2)
Пивкин ИКС-34 (2) Приёмы устных вычислений вида 240 умножить на 4, 203 умножить на 4
Приёмы устных вычислений вида 240 умножить на 4, 203 умножить на 4 Powtórzenie do klasówki
Powtórzenie do klasówki Сложение натуральных чисел 5 класс МОУ «Усть-Мосихинская СОШ» Новосёлова Е.А.
Сложение натуральных чисел 5 класс МОУ «Усть-Мосихинская СОШ» Новосёлова Е.А. Теорема Безу. Схема Горнера
Теорема Безу. Схема Горнера