Содержание
- 2. Random Variable A random variable x takes on a defined set of values with different probabilities.
- 3. Random variables can be discrete or continuous Discrete random variables have a countable number of outcomes
- 4. Probability functions A probability function maps the possible values of x against their respective probabilities of
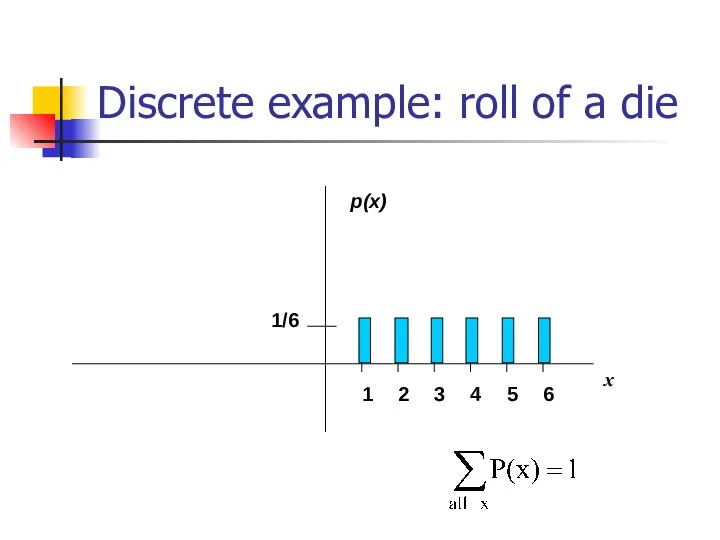
- 5. Discrete example: roll of a die
- 6. Probability mass function (pmf)
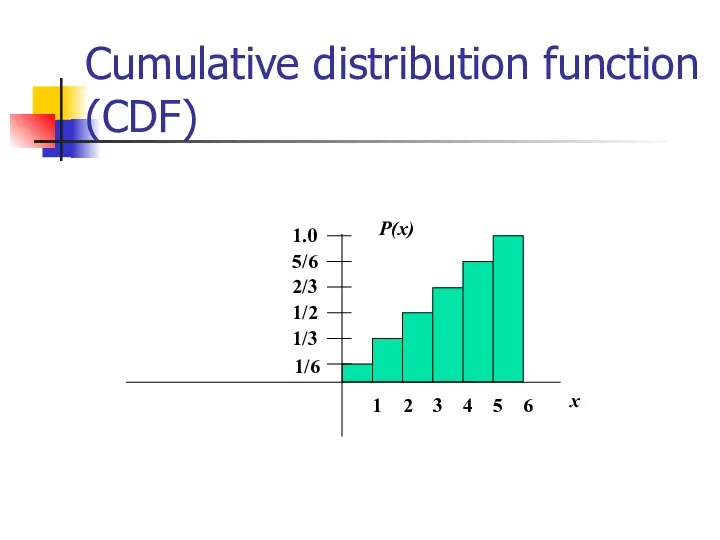
- 7. Cumulative distribution function (CDF)
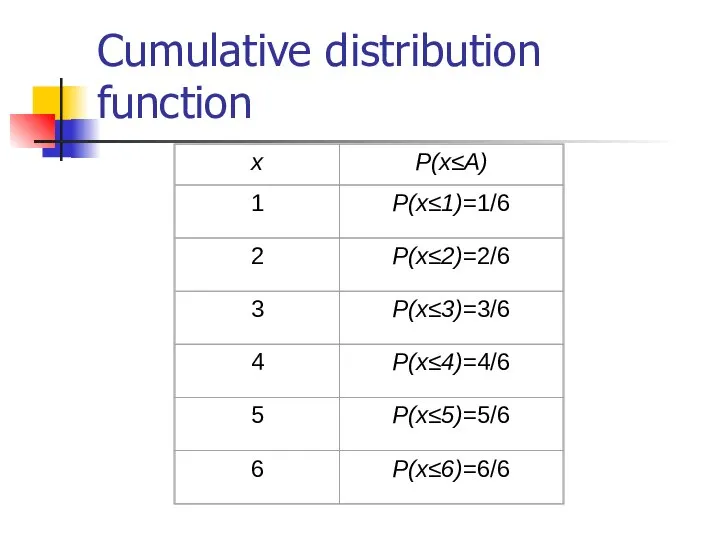
- 8. Cumulative distribution function
- 9. Examples 1. What’s the probability that you roll a 3 or less? P(x≤3)=1/2 2. What’s the
- 10. Practice Problem Which of the following are probability functions? a. f(x)=.25 for x=9,10,11,12 b. f(x)= (3-x)/2
- 11. Answer (a) a. f(x)=.25 for x=9,10,11,12 1.0
- 12. Answer (b) b. f(x)= (3-x)/2 for x=1,2,3,4
- 13. Answer (c) c. f(x)= (x2+x+1)/25 for x=0,1,2,3
- 14. Practice Problem: The number of ships to arrive at a harbor on any given day is
- 15. Practice Problem: You are lecturing to a group of 1000 students. You ask them to each
- 16. Important discrete distributions in epidemiology… Binomial Yes/no outcomes (dead/alive, treated/untreated, smoker/non-smoker, sick/well, etc.) Poisson Counts (e.g.,
- 17. Continuous case The probability function that accompanies a continuous random variable is a continuous mathematical function
- 18. Continuous case For example, recall the negative exponential function (in probability, this is called an “exponential
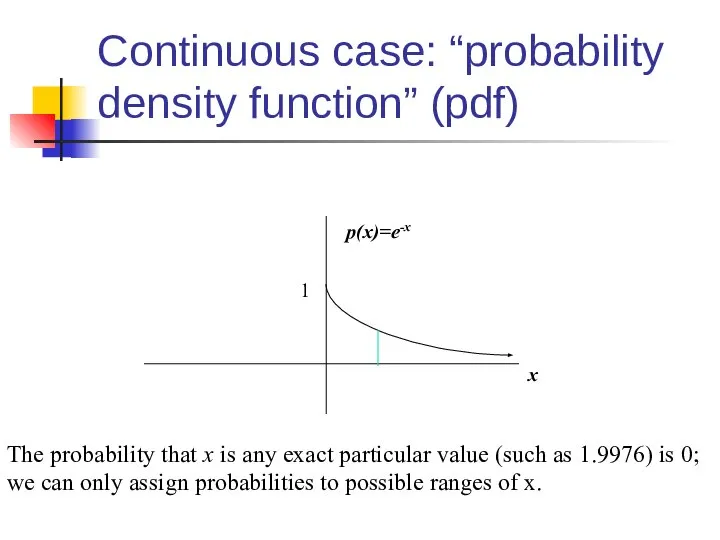
- 19. Continuous case: “probability density function” (pdf) The probability that x is any exact particular value (such
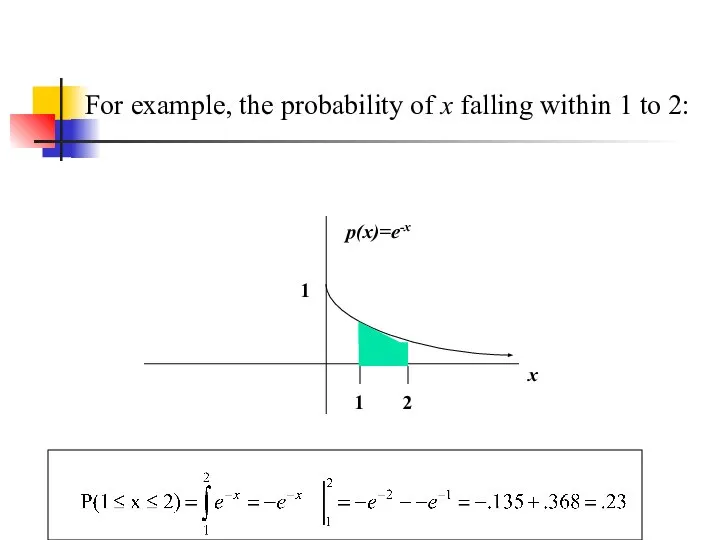
- 20. For example, the probability of x falling within 1 to 2:
- 21. Cumulative distribution function As in the discrete case, we can specify the “cumulative distribution function” (CDF):
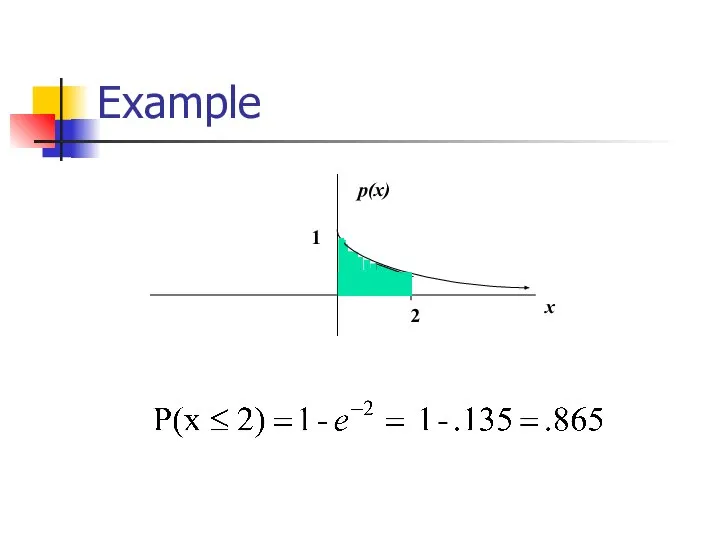
- 22. Example
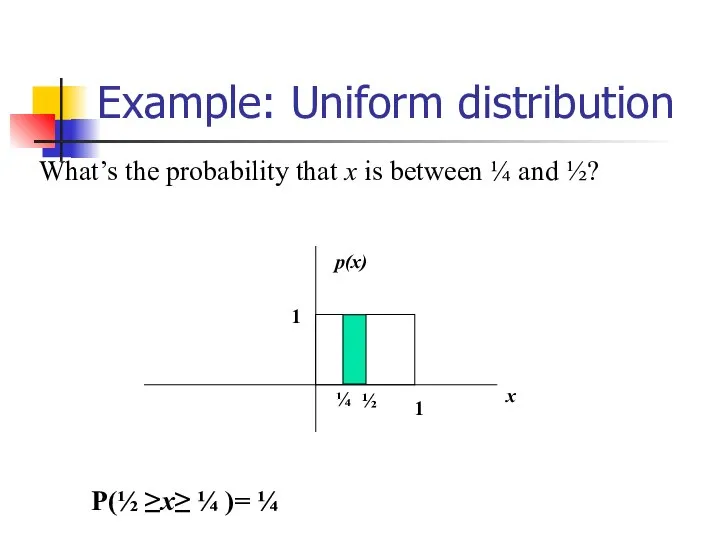
- 23. Example 2: Uniform distribution The uniform distribution: all values are equally likely The uniform distribution: f(x)=
- 24. Example: Uniform distribution What’s the probability that x is between ¼ and ½? P(½ ≥x≥ ¼
- 25. Practice Problem 4. Suppose that survival drops off rapidly in the year following diagnosis of a
- 26. Answer The probability of dying within 1 year can be calculated using the cumulative distribution function:
- 27. Expected Value and Variance All probability distributions are characterized by an expected value and a variance
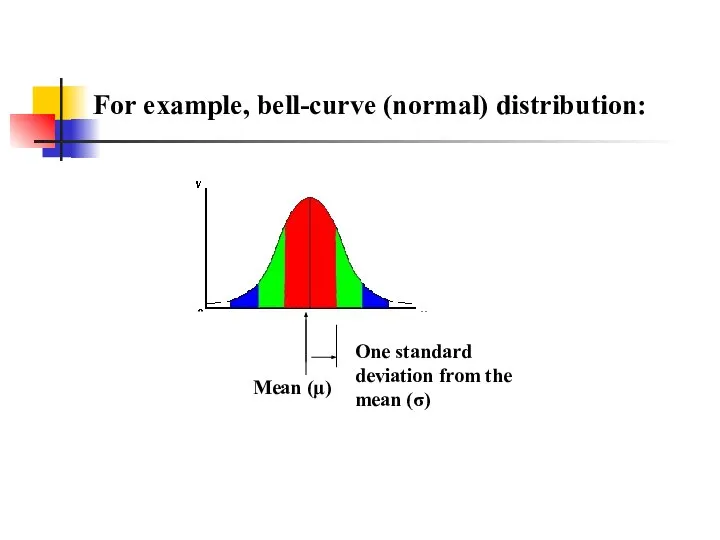
- 28. For example, bell-curve (normal) distribution:
- 29. Expected value, or mean If we understand the underlying probability function of a certain phenomenon, then
- 30. Example: expected value Recall the following probability distribution of ship arrivals:
- 31. Expected value, formally Discrete case: Continuous case:
- 32. Empirical Mean is a special case of Expected Value… Sample mean, for a sample of n
- 33. Expected value, formally Discrete case: Continuous case:
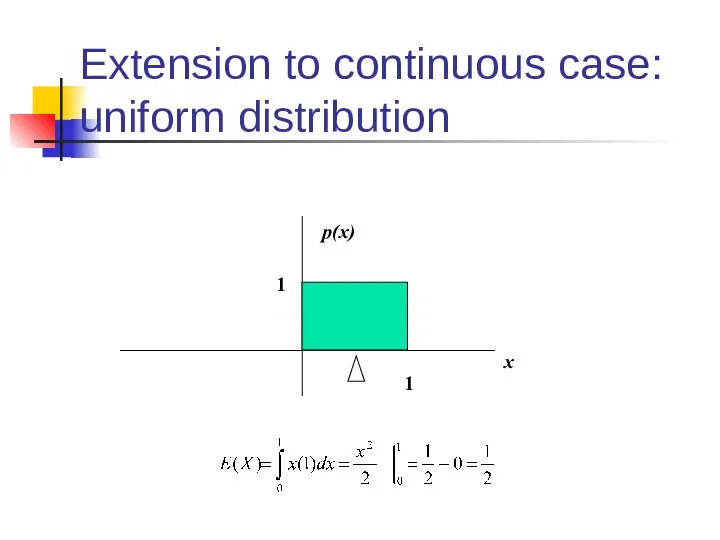
- 34. Extension to continuous case: uniform distribution x p(x) 1 1
- 35. Symbol Interlude E(X) = µ these symbols are used interchangeably
- 36. Expected Value Expected value is an extremely useful concept for good decision-making!
- 37. Example: the lottery The Lottery (also known as a tax on people who are bad at
- 38. Lottery Calculate the probability of winning in 1 try: The probability function (note, sums to 1.0):
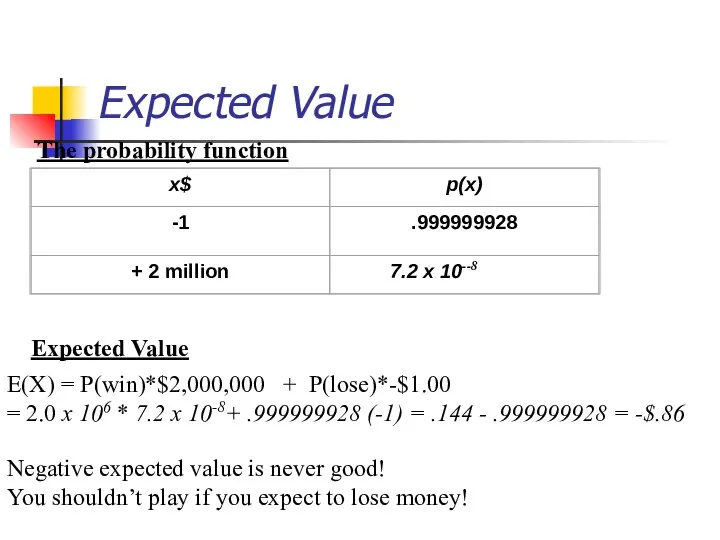
- 39. Expected Value The probability function Expected Value E(X) = P(win)*$2,000,000 + P(lose)*-$1.00 = 2.0 x 106
- 40. Expected Value If you play the lottery every week for 10 years, what are your expected
- 41. Gambling (or how casinos can afford to give so many free drinks…) A roulette wheel has
- 42. **A few notes about Expected Value as a mathematical operator: If c= a constant number (i.e.,
- 43. E(c) = c E(c) = c Example: If you cash in soda cans in CA, you
- 44. E(cX)=cE(X) E(cX)=cE(X) Example: If the casino charges $10 per game instead of $1, then the casino
- 45. E(c + X)=c + E(X) E(c + X)=c + E(X) Example, if the casino throws in
- 46. E(X+Y)= E(X) + E(Y) E(X+Y)= E(X) + E(Y) Example: If you play the lottery twice, you
- 47. Practice Problem If a disease is fairly rare and the antibody test is fairly expensive, in
- 48. Answer (a) a. Suppose a particular disease has a prevalence of 10% in a third-world population
- 49. Answer (b) b. What if you pool only 10 samples at a time? E(X) = (.90)10
- 50. Answer (c) c. 5 samples at a time? E(X) = (.90)5 (1) + [1-.905] (6) =
- 51. Practice Problem If X is a random integer between 1 and 10, what’s the expected value
- 52. Answer If X is a random integer between 1 and 10, what’s the expected value of
- 53. Expected value isn’t everything though… Take the show “Deal or No Deal” Everyone know the rules?
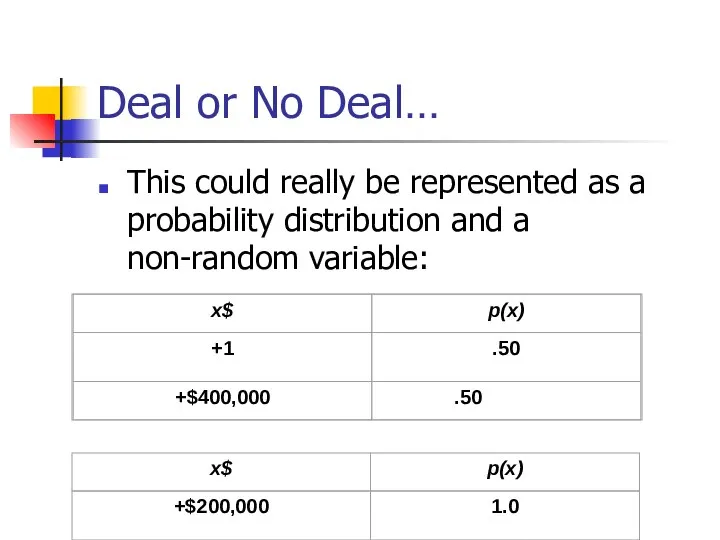
- 54. Deal or No Deal… This could really be represented as a probability distribution and a non-random
- 55. Expected value doesn’t help…
- 56. How to decide? Variance! If you take the deal, the variance/standard deviation is 0. If you
- 57. Variance/standard deviation “The average (expected) squared distance (or deviation) from the mean” **We square because squaring
- 58. Variance, formally Discrete case: Continuous case:
- 59. Similarity to empirical variance The variance of a sample: s2 =
- 60. Symbol Interlude Var(X) = σ2 these symbols are used interchangeably
- 61. Variance: Deal or No Deal Now you examine your personal risk tolerance…
- 62. Practice Problem A roulette wheel has the numbers 1 through 36, as well as 0 and
- 63. Answer Standard deviation is $.99. Interpretation: On average, you’re either 1 dollar above or 1 dollar
- 64. Handy calculation formula! Handy calculation formula (if you ever need to calculate by hand!):
- 65. Var(x) = E(x-μ)2 = E(x2) – [E(x)]2 (your calculation formula!) Proofs (optional!): E(x-μ)2 = E(x2–2μx +
- 66. For example, what’s the variance and standard deviation of the roll of a die?
- 67. **A few notes about Variance as a mathematical operator: If c= a constant number (i.e., not
- 68. Var(c) = 0 Var(c) = 0 Constants don’t vary!
- 69. Var (c+X)= Var(X) Var (c+X)= Var(X) Adding a constant to every instance of a random variable
- 70. Var (c+X)= Var(X) Var (c+X)= Var(X) Adding a constant to every instance of a random variable
- 71. Var(cX)= c2Var(X) Var(cX)= c2Var(X) Multiplying each instance of the random variable by c makes it c-times
- 72. Var(X+Y)= Var(X) + Var(Y) Var(X+Y)= Var(X) + Var(Y) ONLY IF X and Y are independent!!!!!!!! With
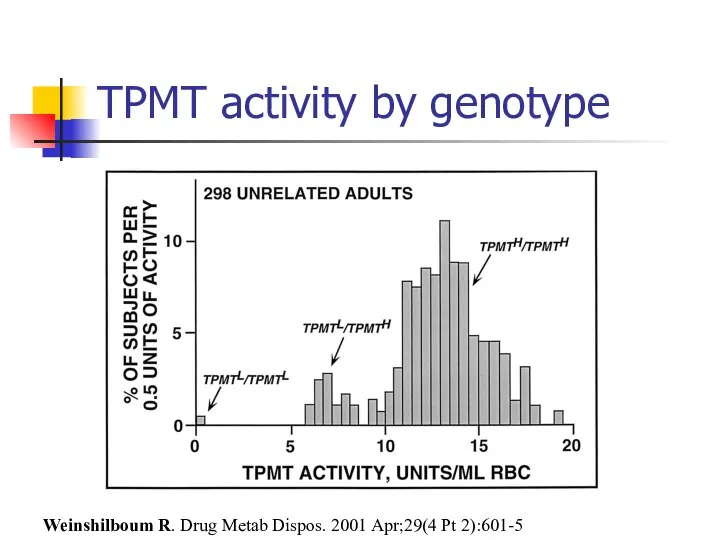
- 73. Example of Var(X+Y)= Var(X) + Var(Y): TPMT TPMT metabolizes the drugs 6- mercaptopurine, azathioprine, and 6-thioguanine
- 74. TPMT activity by genotype Weinshilboum R. Drug Metab Dispos. 2001 Apr;29(4 Pt 2):601-5
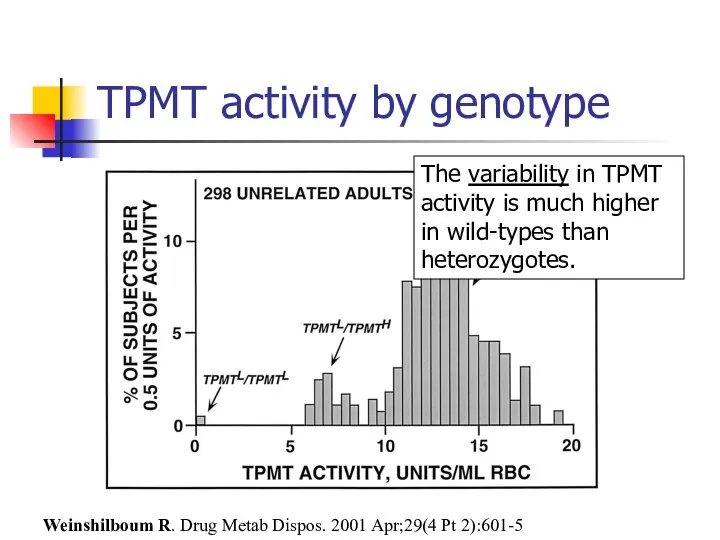
- 75. TPMT activity by genotype Weinshilboum R. Drug Metab Dispos. 2001 Apr;29(4 Pt 2):601-5 The variability in
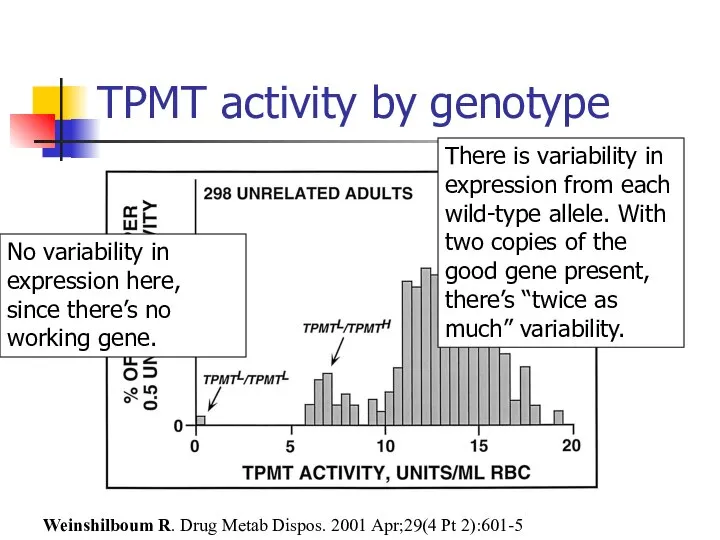
- 76. TPMT activity by genotype Weinshilboum R. Drug Metab Dispos. 2001 Apr;29(4 Pt 2):601-5 There is variability
- 77. Practice Problem Find the variance and standard deviation for the number of ships to arrive at
- 78. Answer: variance and std dev Interpretation: On an average day, we expect 11.3 ships to arrive
- 79. Practice Problem You toss a coin 100 times. What’s the expected number of heads? What’s the
- 80. Answer: expected value Intuitively, we’d probably all agree that we expect around 50 heads, right? Another
- 81. Answer: variance What’s the variability, though? More tricky. But, again, we could do this for 1
- 82. Or use computer simulation… Flip coins virtually! Flip a virtual coin 100 times; count the number
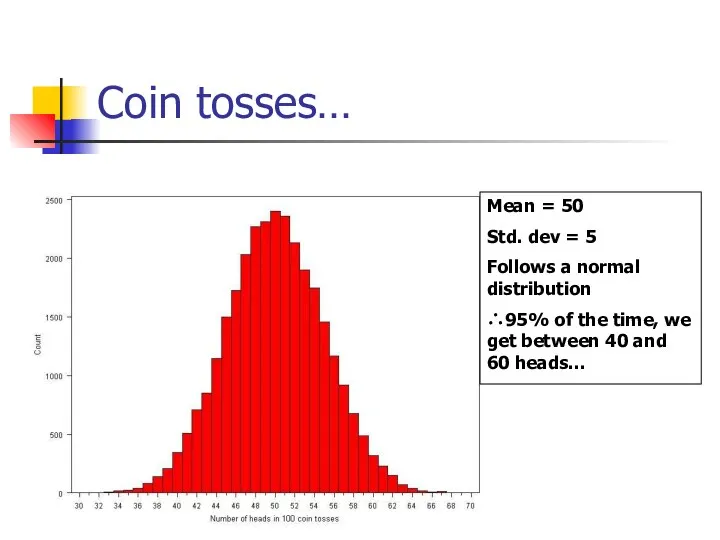
- 83. Coin tosses… Mean = 50 Std. dev = 5 Follows a normal distribution ∴95% of the
- 84. Covariance: joint probability The covariance measures the strength of the linear relationship between two variables The
- 85. The Sample Covariance The sample covariance:
- 87. Скачать презентацию

































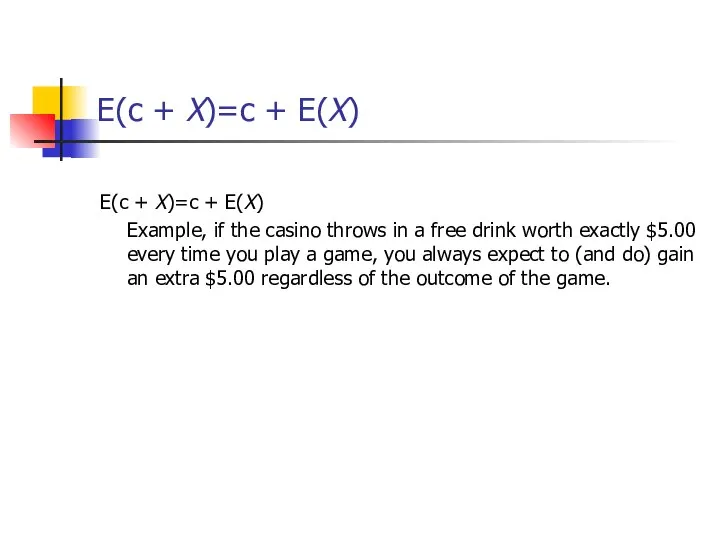


















![Var(x) = E(x-μ)2 = E(x2) – [E(x)]2 (your calculation formula!) Proofs (optional!):](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1058868/slide-64.jpg)






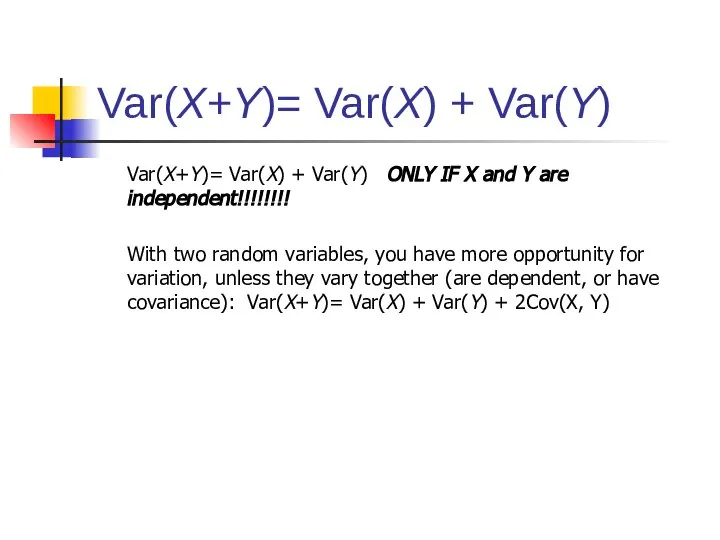









 Дифференцирование показательной и логарифмической функций
Дифференцирование показательной и логарифмической функций В стране геометрических фигур (форма, размер, цвет)
В стране геометрических фигур (форма, размер, цвет) Арифметический квадратный корень
Арифметический квадратный корень Натуральные числа и дроби. Урок 1
Натуральные числа и дроби. Урок 1 Круговая окружность
Круговая окружность Среднее арифметическое
Среднее арифметическое Презентация на тему Перевод целых чисел в 2, 8, 16-ую системы счисления
Презентация на тему Перевод целых чисел в 2, 8, 16-ую системы счисления 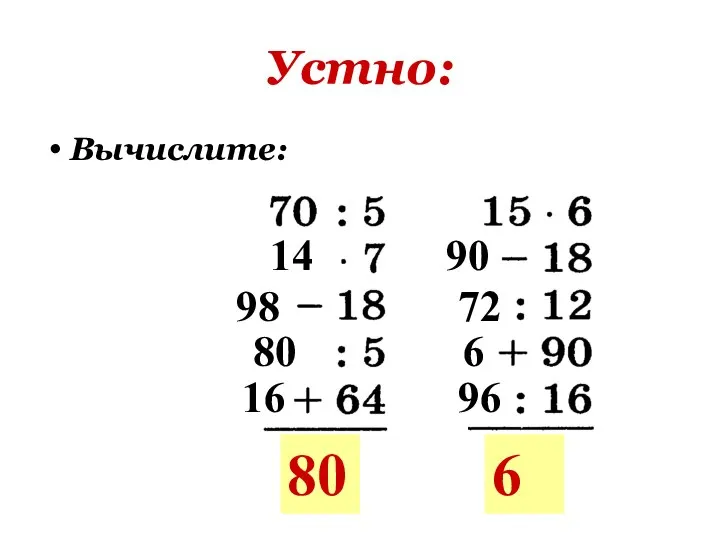 Устно. Вычисления
Устно. Вычисления Презентация на тему Умножение и деление десятичной дроби на 10, 100, 1000 и т.д.
Презентация на тему Умножение и деление десятичной дроби на 10, 100, 1000 и т.д.  lobachevsky
lobachevsky Сложение и вычитание положительных десятичных дробей
Сложение и вычитание положительных десятичных дробей Золотое сечение
Золотое сечение Арифметическая прогрессия
Арифметическая прогрессия Взаимно обратные числа
Взаимно обратные числа Теорема Пифагора
Теорема Пифагора Статистические графики
Статистические графики ложение комплексных чисел. Вычитание комплексных чисел
ложение комплексных чисел. Вычитание комплексных чисел Булева алгебра
Булева алгебра Зимующие птицы. Дети 5 лет
Зимующие птицы. Дети 5 лет Числа от 1 до 100. Умножение и деление. Закрепление
Числа от 1 до 100. Умножение и деление. Закрепление Задания по математике (5 класс, часть 7)
Задания по математике (5 класс, часть 7) Геометрический смысл производной
Геометрический смысл производной Векторы на плоскости
Векторы на плоскости Интерактивный тренажёр. Сложение и вычитание в пределах первого десятка. 3 уровень
Интерактивный тренажёр. Сложение и вычитание в пределах первого десятка. 3 уровень Синус, косинус и тангенс угла
Синус, косинус и тангенс угла Курс по математике ОГЭ 2021
Курс по математике ОГЭ 2021 Проценты (1)
Проценты (1) Деление обыкновенных дробей
Деление обыкновенных дробей