Содержание
- 2. Вспомним:
- 3. Постараемся ввести степень с отрицательным показателем так, чтобы свойства для степени с натуральным показателем остались верными
- 4. Сначала введём степень с показателем 0. Для этого в свойстве 2 положим m=n : ВЫВОД:
- 5. Теперь в свойстве 2 положим m=0 :
- 6. определение степени с отрицательным показателем:
- 9. Скачать презентацию





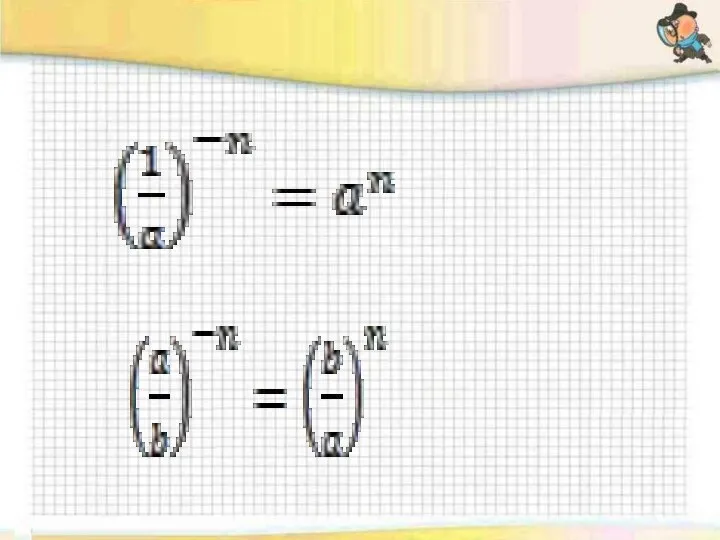
 Дифференциальные уравнения
Дифференциальные уравнения Показательные уравнения
Показательные уравнения Стандартный вид числа в физике, астрономии и технике
Стандартный вид числа в физике, астрономии и технике Основное свойство дроби
Основное свойство дроби Решение уравнений. Математика 6 класс
Решение уравнений. Математика 6 класс Нахождение угла между двумя прямыми в пространстве
Нахождение угла между двумя прямыми в пространстве Понятие вектора
Понятие вектора Прогрессии в окружающей нас жизни
Прогрессии в окружающей нас жизни Погрешность измерения
Погрешность измерения Порог чувствительности средства измерений
Порог чувствительности средства измерений Порядок действий в выражениях со скобками
Порядок действий в выражениях со скобками Правильные многогранники
Правильные многогранники Таблица умножения на 3 в стихах
Таблица умножения на 3 в стихах Область определения и множество значений тригонометрических функций
Область определения и множество значений тригонометрических функций Длина окружности
Длина окружности Корень n-ой степени и его свойства
Корень n-ой степени и его свойства Рациональные дроби и их свойства
Рациональные дроби и их свойства Исследовательская работа. Теорема Пифагора
Исследовательская работа. Теорема Пифагора Линейные однородные дифференциальные уравнения. Формула Остроградского-Лиувилля
Линейные однородные дифференциальные уравнения. Формула Остроградского-Лиувилля Понятие движения. Геометрия 9 класс
Понятие движения. Геометрия 9 класс Сложение и вычитание обыкновенных дробей. Графический диктант
Сложение и вычитание обыкновенных дробей. Графический диктант Поворот точки вокруг начала координат
Поворот точки вокруг начала координат Многоугольники в жизни. Примеры
Многоугольники в жизни. Примеры Математический кроссворд. Для учащихся 5-6 классов
Математический кроссворд. Для учащихся 5-6 классов Парный регрессионный анализ
Парный регрессионный анализ Логарифм
Логарифм Понятие многогранник, призма
Понятие многогранник, призма Статистика, часть 6. Условные обозначения
Статистика, часть 6. Условные обозначения