Содержание
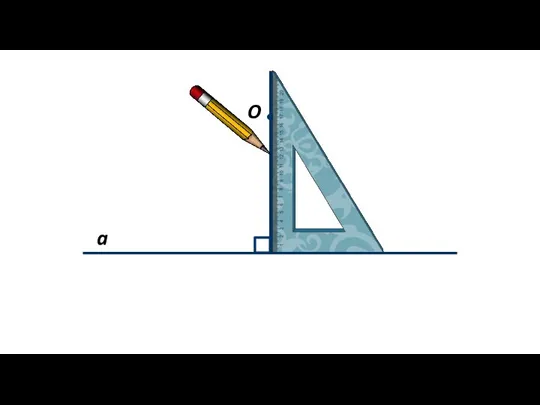
- 2. Отрезок ОВ называется перпендикуляром, проведённым из точки О к прямой а, если отрезок ОВ и прямая
- 3. Доказательство. 1. Существование. Теорема. Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой,
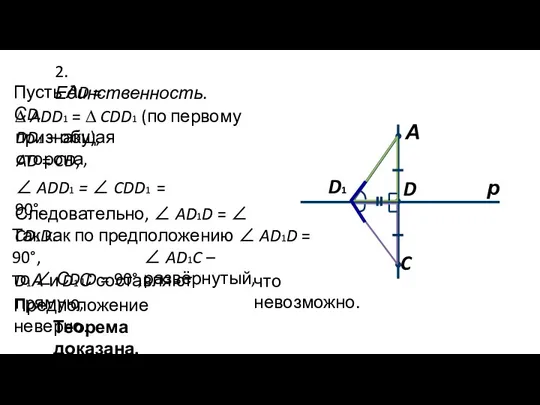
- 4. AD = CD, Так как по предположению ∠ AD1D = 90°, то ∠ СD1D = 90°,
- 7. Скачать презентацию


 Обобщение по 3-м формулам сокращенного умножения
Обобщение по 3-м формулам сокращенного умножения Сложение отрицательных чисел
Сложение отрицательных чисел Презентация на тему Разность и её значение (1 класс)
Презентация на тему Разность и её значение (1 класс)  Весёлая математика: Давайте посчитаем
Весёлая математика: Давайте посчитаем Презентация на тему Комплексные числа 11 класс
Презентация на тему Комплексные числа 11 класс  Первообразная и интеграл
Первообразная и интеграл Основы математической статистики
Основы математической статистики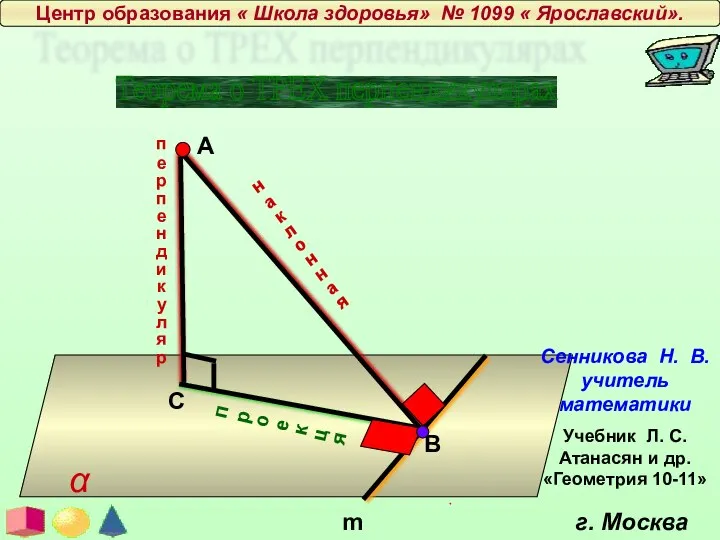 Теорема о трех перпендикулярах
Теорема о трех перпендикулярах Пересечение поверхностей, одна из которых занимает проецирующее положение относительно плоскости проекций
Пересечение поверхностей, одна из которых занимает проецирующее положение относительно плоскости проекций Многогранники в природе
Многогранники в природе теория вероятностей задачи
теория вероятностей задачи Задача по математике (4 класс, задание 85.1)
Задача по математике (4 класс, задание 85.1) Вычисление вероятностей сложных событий
Вычисление вероятностей сложных событий Ряды распределения в статистике
Ряды распределения в статистике Л 5 Функция одной переменной
Л 5 Функция одной переменной Повторение пройденного (1 класс)
Повторение пройденного (1 класс) Исследование функции с помощью производной
Исследование функции с помощью производной Свойство параллелограмма
Свойство параллелограмма ВПР вариант 16 № 11. Решение трудной задачи
ВПР вариант 16 № 11. Решение трудной задачи Презентация на тему Тетраэдр (10 класс)
Презентация на тему Тетраэдр (10 класс)  Презентация на тему Умножение и деление чисел на 2 и на 3 (2 класс)
Презентация на тему Умножение и деление чисел на 2 и на 3 (2 класс)  ЕГЭ 2012
ЕГЭ 2012 Многоугольники в нашей жизни
Многоугольники в нашей жизни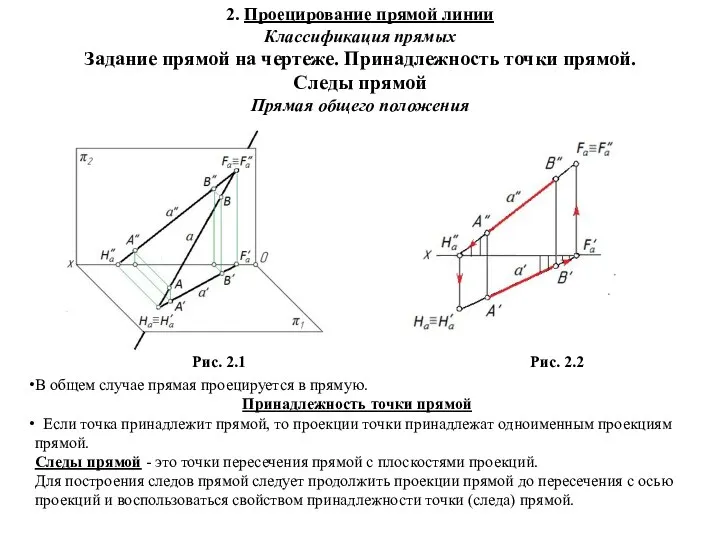 Начертательная геометрия. Проецирование прямой линии
Начертательная геометрия. Проецирование прямой линии Контрольная работа. 8 класс
Контрольная работа. 8 класс Множества натуральных чисел
Множества натуральных чисел Первый признак параллельности прямых
Первый признак параллельности прямых Прикладная математика. Лекция 1. Геометрический метод решения задачи линейного программирования
Прикладная математика. Лекция 1. Геометрический метод решения задачи линейного программирования