Решение систем линейных алгебраических уравнений

Малые погрешности в вычислениях могут привести к большим погрешностям в решении, и задача решения СЛАУ является неустойчивой.

ЧИСЛО ОБУСЛОВЛЕННОСТИ cond(A)
При численном решении различных прикладных задач исследователи часто сталкиваются с таким понятием как число обусловленности. Это понятие описывается в учебниках по матричной алгебре. Число обусловленности является важнейшим «индикатором» для определения устойчивости решения той или иной задачи.
Известные американские математики Форсайт и Молер по поводу числа обусловленности пишут следующее: «Широко распространено заблуждение, что малость det(A) влечет за собой плохую обусловленность матрицы А». Далее, «… значение cond(A) является гораздо более важным критерием трудности решения линейной системы Ax=b, чем малость det(A), либо громадность порядка n».

Обусловленность оценивает близость матрицы коэффициентов А к вырожденной.
Число обусловленности cond(A) является количественной оценкой обусловленности.
Всегда cond(A)≥1.

Если cond(A)≥103, то говорят, что матрица А плохо обусловлена.
Если 1≤cond(A)≤100, то матрица считается хорошо обусловленной.
Причина появления больших погрешностей при решении плохо обусловленных систем хорошо иллюстрируется на примере следующей системы линейных алгебраических уравнений (СЛАУ) с двумя неизвестными:

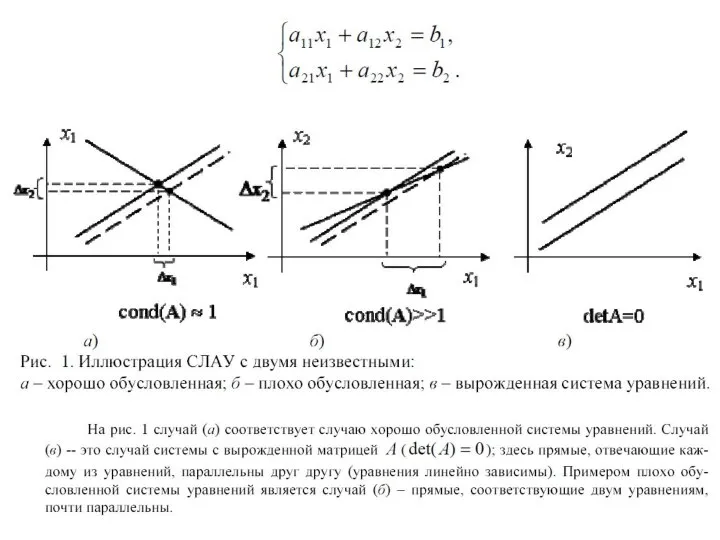
На рис. 1 случай (а) соответствует случаю хорошо обусловленной системы уравнений.
Случай (в) -- это случай системы с вырожденной матрицей А (det(A)=0); здесь прямые, отвечающие каждому из уравнений, параллельны друг другу (уравнения линейно зависимы).
Примером плохо обусловленной системы уравнений является случай (б) – прямые, соответствующие двум уравнениям, почти параллельны.

Штриховые прямые (а) и (б) на рис. 1 отвечают одному из уравнений, в котором немного изменены коэффициенты aij или правая часть bj.
Как видно, в случае хорошо обусловленной СЛАУ малые возмущения в величинах aij и bi приводят к небольшим изменениям решения (точка пересечения прямых смещается незначительно).
В случае плохо обусловленной системы уравнений малые изменения в коэффициентах ведут к большим изменениям в решении (точка пересечения прямых смещается сильно).

Число обусловленности матрицы и устойчивость решения системы уравнений
Система уравнений считается хорошо обусловленной, если малые изменения в коэффициентах матрицы или в правой части вызывают малые изменения в решении.
Система уравнений считается плохо обусловленной, если малые изменения в коэффициентах матрицы или в правой части вызывают большие изменения в решении.
Рассмотрим несколько примеров [2].

Пример 1. Дана система уравнений:
Решением уравнения (1) является следующее:
Теперь внесем небольшие изменения в правую часть системы (1):
Решением системы (2) является

Если теперь внесем малые изменения в коэффициентах системы (1)
То получим следующее решение
Очевидно, система (1) является «плохо обусловленной», так как малые изменения, внесенные в коэффициентах матрицы или в правую часть, повлекли за собой большие изменения в решении системы.

Как видно, система (4) является «хорошо обусловленной», так как малые изменения, внесенные в коэффициентах матрицы или в правую часть, повлекли за собой малые изменения в решении системы.
Эти простые примеры показывают, насколько небольшие изменения коэффициентов матрицы или правой части (вызванные различными источниками погрешности: ошибки округления, погрешности различных численных методов и т.д.) могут существенно изменить решение. И, действительно, с этой проблемой исследователи часто сталкиваются при численном решении различных прикладных задач.

Теперь рассмотрим, как можно вычислить число обусловленности матрицы.
Число обусловленности матрицы напрямую связано с понятием норма матрицы.
Как и определитель квадратной матрицы, норма матрицы – это число (скаляр).
Норма матрицы (квадратной, прямоугольной, обратимой или необратимой) всегда является положительным числом.

Понятие нормы универсально для любой матрицы, квадратной или неквадратной, матрицы-столбца или строки, размерность также может быть любой.
Эту характеристику используют в качестве оценочной величины для анализа изменяемости матрицы в каком-либо расчетном процессе или совокупности нескольких матриц.

Можно сказать, что норма является показателем «мощности» матрицы.
Она обозначается ‖A‖ и равна действительному числу, которое должно соответствовать определенному набору условий:

Существует три вида норм: бесконечная, первая норма и вторая (евклидова).
Все они являются каноническими, т.е. их значения не меньше по модулю любого матричного элемента. На практике обычно вычисляют только один из видов, этого достаточно для объективной оценки.

Чтобы найти норму матрицы, нужно воспользоваться одним из ниже приведенных способов для каждого вида. Все они основаны на расчете суммы элементов матрицы, но каждый подразумевает собственный алгоритм
Для расчета бесконечной нормы просуммируйте по модулю значения элементов отдельно по каждой строке и выберите из них максимальное
Найдите первую норму, поступив аналогично с элементами по каждому столбцу
Расчет евклидовой нормы подразумевает три действия: возведение каждого элемента в квадрат, суммирование и извлечение квадратной корня из общего результата

Пример: вычислите все виды норм для данной матрицы.

Решение
a11+a12=11;
a21+a22=12;
a31+a32=5 → ‖А‖∞ = 12;

Решение
2) a11+a21+a31=12;
a12+a22+а32=16
‖А‖1 = 16;

Определим зависимость числа обусловленности от нормы матрицы
Вернемся к рассмотрению плохо обусловленной системы (1)
Запишем систему (1) в новых обозначениях

Обозначим систему (2) так:
После внесения малых изменений в правую часть системы (1) мы получили систему (2)

Найдем изменение правой части и решения

Изменение правой части равно:

Изменение решения равно:

Эта связь выражается в следующих неравенствах:

пропустить

Если учесть, что при представлении вещественных чисел на ЭВМ используются 24 значащие цифры, то машинная погрешность равна:
Таким образом, в векторе решения будем иметь не более двух верных цифр после запятой.
Итак, понятие числа обусловленности очень важно при решении различных прикладных задач.
Число обусловленности является более важным критерием плохой обусловленности СЛАУ, чем малость определителя матрицы или ее большой порядок.
пропустить

Понятие числа обусловленности очень важно при решении различных прикладных задач.
Число обусловленности является более важным критерием плохой обусловленности СЛАУ, чем малость определителя матрицы или ее большой порядок.

Итак, чем больше число обусловленности, тем сильнее сказывается на решении линейной системы ошибка в исходных данных.

Решение СЛАУ

Итак, обычно СЛАУ n-го порядка записывается в виде
или в развернутой форме

К прямым (точным) методам относятся такие методы, которые, в предположении, что вычисления ведутся без округлений, позволяют получить точные значения неизвестных за конечное число арифметических операций.
Они просты, универсальны и используются для широкого класса систем. Однако они не применимы к системам больших порядков (n < 200) и к плохо обусловленным системам из-за возникновения больших погрешностей.

К ним можно отнести:
правило Крамера,
метод обратных матриц,
метод последовательного исключения неизвестных (метод Гаусса),
метод Холецкого,
метод LU-разложения (использование мультипликативных разложений матриц),
метод прогонки,
метод квадратного корня, метод наименьших квадратов и др.

К приближенным относятся методы, которые даже в предположении, что вычисления ведутся без округлений, позволяют получить решение системы лишь с заданной точностью. Это итерационные методы (методы последовательных приближений) позволяют получать решение систем с помощью бесконечных сходящихся процессов.

К таким методам относятся:
метод итераций (метод последовательных приближений)
метод Зейделя
метод Ричардсона с чебышевским набором параметров
метод минимальных поправок
метод скорейшего спуска
метод релаксации

завершить