Содержание
- 2. План: Роль и место математики в современном мире Понятие функции и способы ее задания Классификация функций
- 3. В любой науке столько истины, сколько в ней математики. И.Кант Роль и место математики в современном
- 4. МАТЕМАТИКА - область человеческого знания, изучающая математические модели, отражающие объективные свойства и связи. Математика (греч. mathematike,
- 5. Современное понятие математики - наука о математических структурах (множествах, между элементами которых определены некоторые отношения).
- 6. 1 период (с древнейших времен до VIII-VII вв до н.э.) – зарождение математики 2 период (с
- 7. 2.Понятие функции и способы ее задания
- 8. Функция – зависимость переменной y от переменной x, при которой каждому значению x соответствует единственное значение
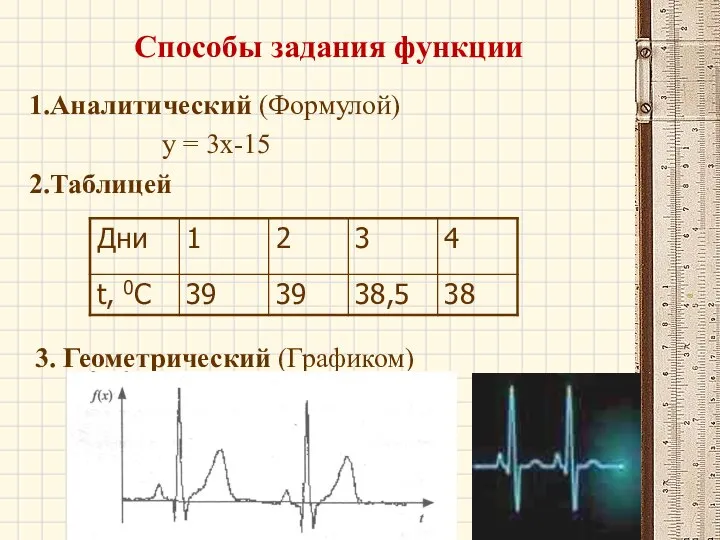
- 9. Способы задания функции 1.Аналитический (Формулой) у = 3х-15 2.Таблицей 3. Геометрический (Графиком)
- 10. Простейшие элементарные функции 3.Классификация функций
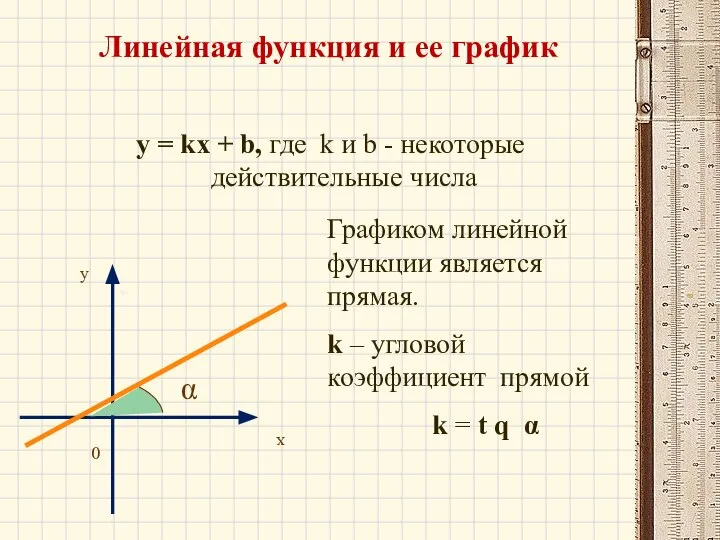
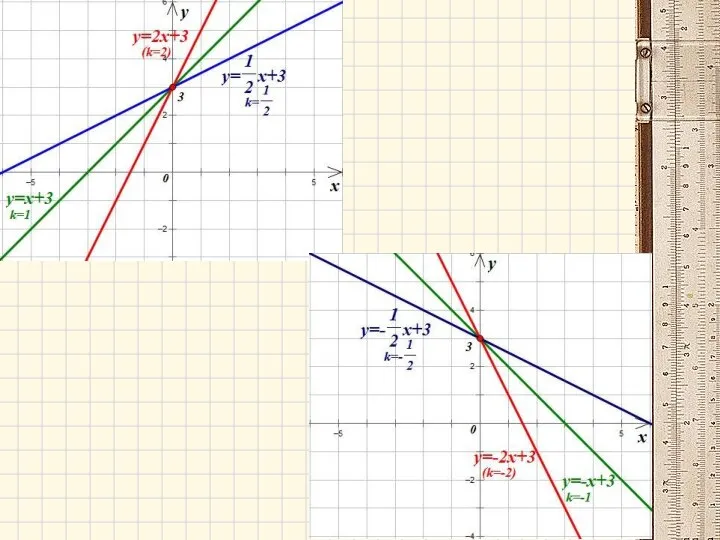
- 11. Линейная функция и ее график y = kx + b, где k и b - некоторые
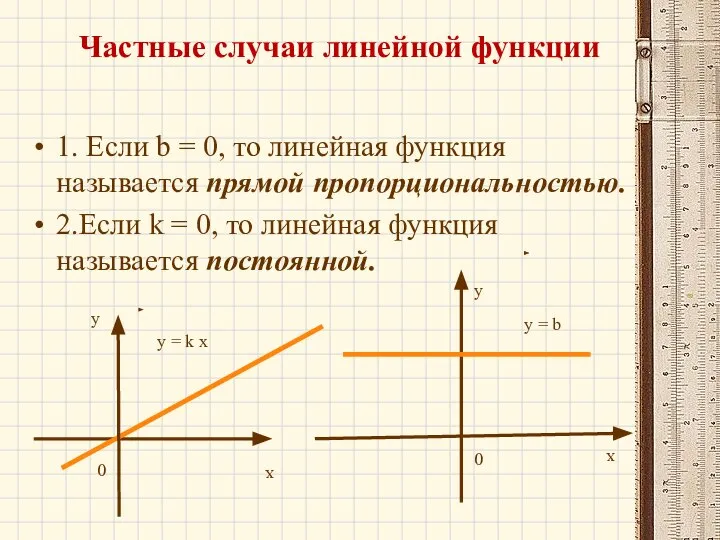
- 13. Частные случаи линейной функции 1. Если b = 0, то линейная функция называется прямой пропорциональностью. 2.Если
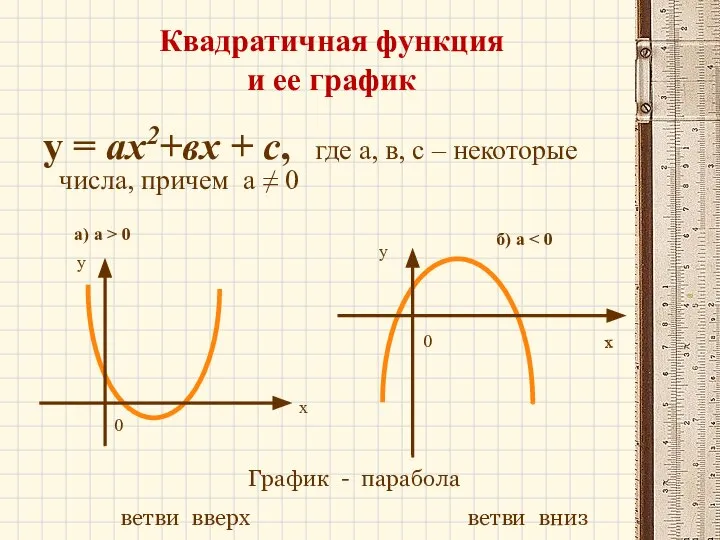
- 14. Квадратичная функция и ее график у = ах2+вх + с, где а, в, с – некоторые
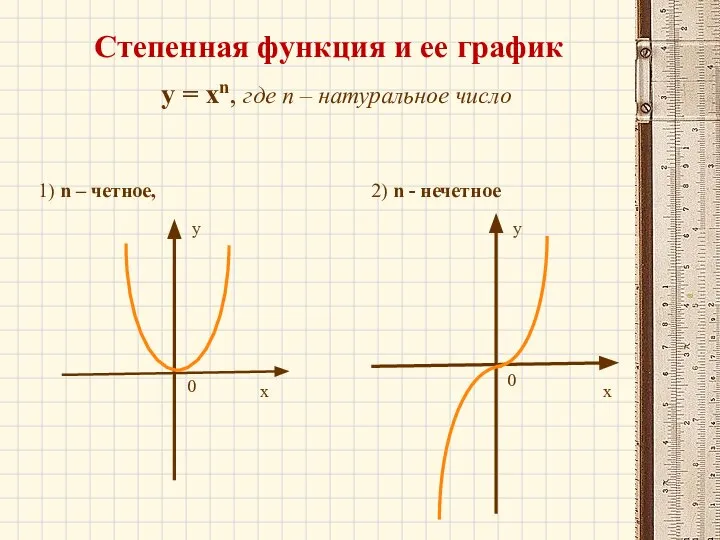
- 15. Степенная функция и ее график y = xn, где n – натуральное число 1) n –
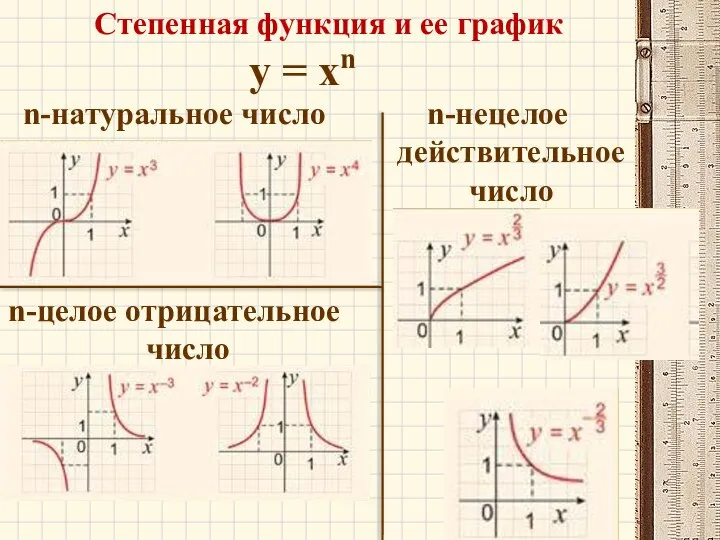
- 16. Степенная функция и ее график y = xn n-натуральное число n-целое отрицательное число n-нецелое действительное число
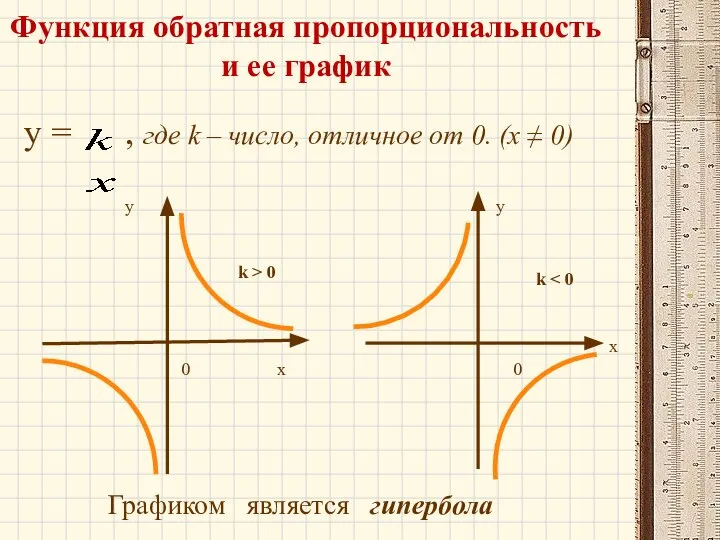
- 17. Функция обратная пропорциональность и ее график y = , где k – число, отличное от 0.
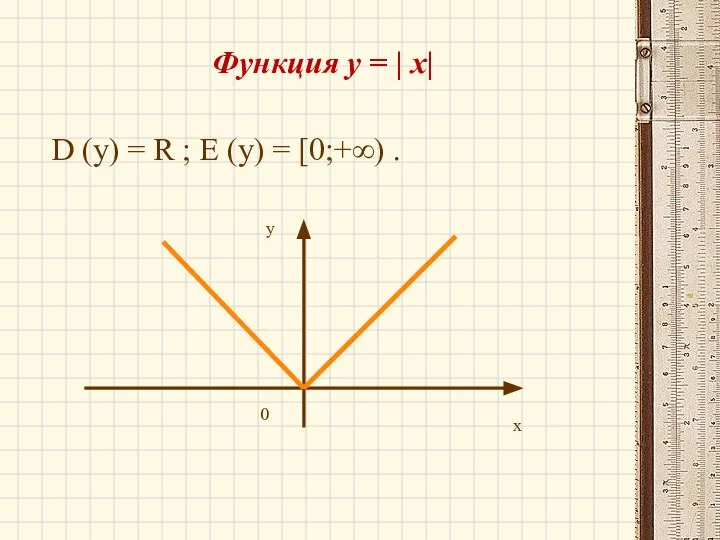
- 18. Функция y = | x| D (y) = R ; E (y) = [0;+∞) . x
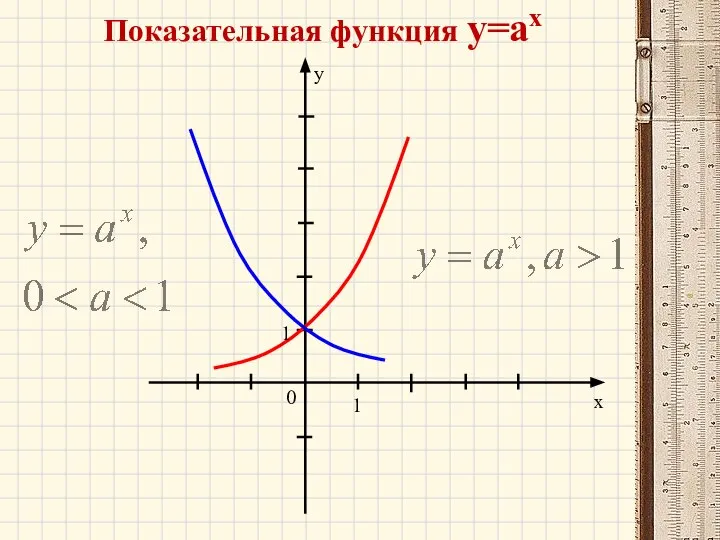
- 19. Показательная функция у=ах 0 x y 1 1
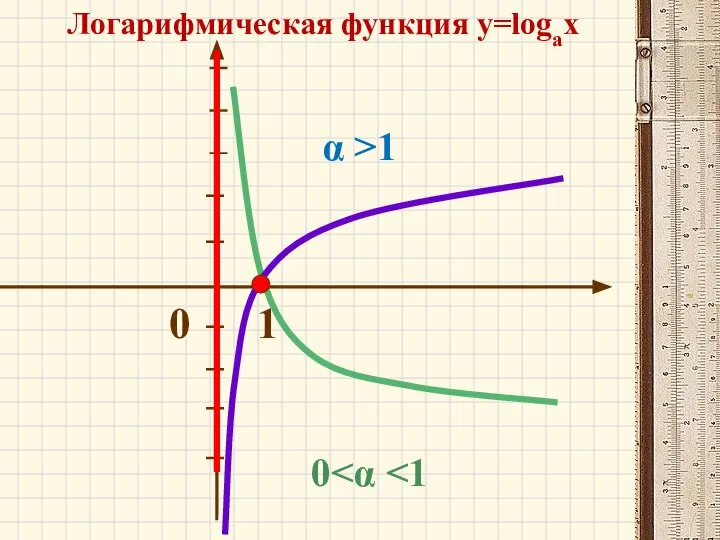
- 20. 0 1 Логарифмическая функция y=logax α >1 0
- 21. Тригонометрические функции
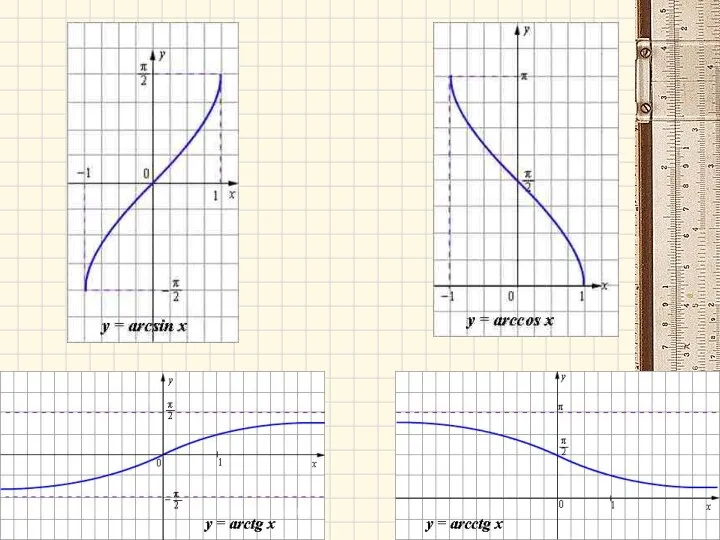
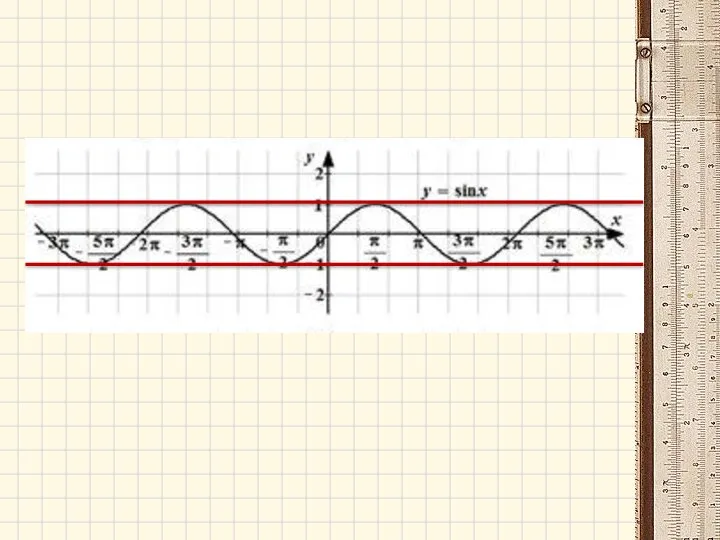
- 22. D(y)=(-∞;+∞) E(y)=[-1;1] Период Т=2π Нечетная функция D(y)=(-∞;+∞) E(y)=[-1;1] Период Т=2π Четная функция E(y)=(-∞;+∞) Период Т=π Нечетная
- 23. Обратные тригонометрические функции
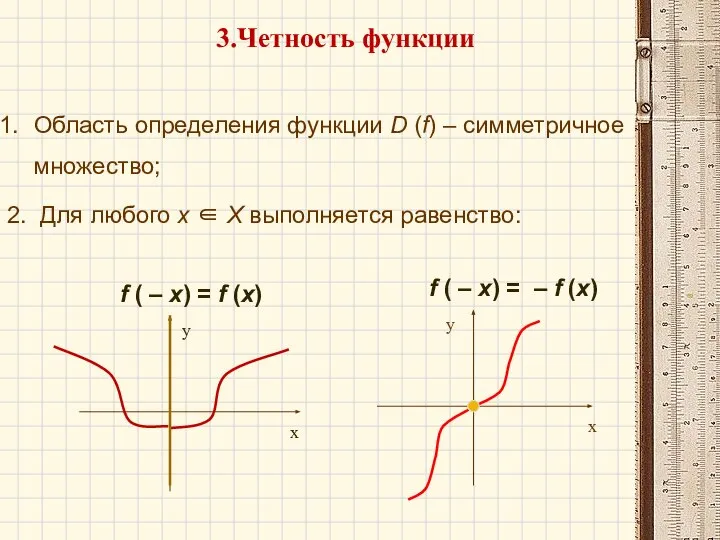
- 25. 4. Свойства функции Область определения функции D(у) Множество значений функции Е(у) Четность функции Промежутки монотонности (промежутки
- 26. 1. Область определения функции – все значения, которые принимает независимая переменная. Обозначается : D (f). 2.Область
- 27. Область определения функции D (f) – симметричное множество; 2. Для любого х ∈ Х выполняется равенство:
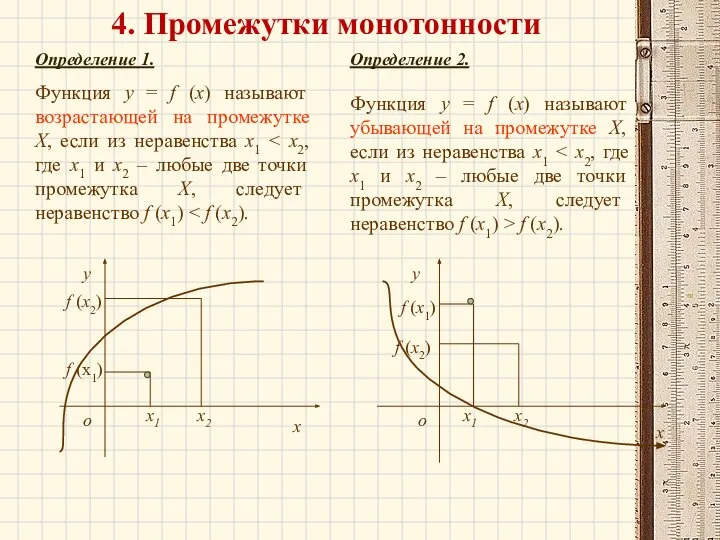
- 28. Определение 1. Функция у = f (х) называют возрастающей на промежутке Х, если из неравенства х1
- 29. ПРИМЕР: Линейная функция у = kx + m. 1. Если k > 0, то функция возрастает
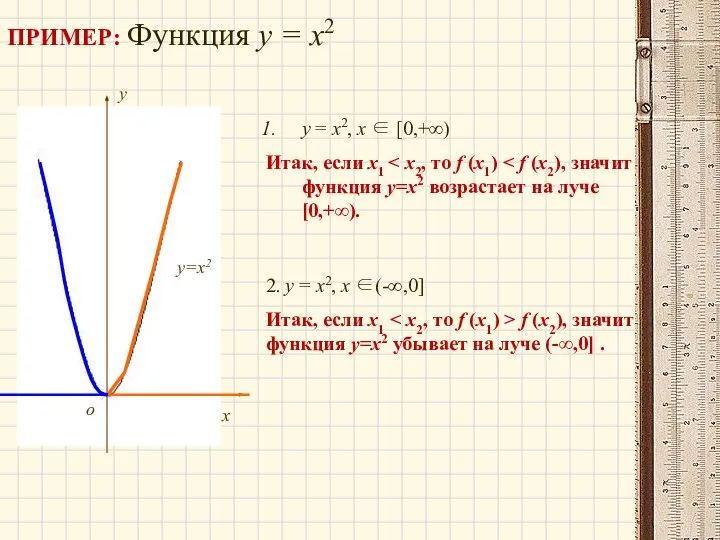
- 30. ПРИМЕР: Функция у = х2 х о у у=х2 у = х2, х ∈ [0,+∞) Итак,
- 31. 5. Ограниченность функции Функция у = f (x) называют ограниченной снизу на множестве Х ⊂ D
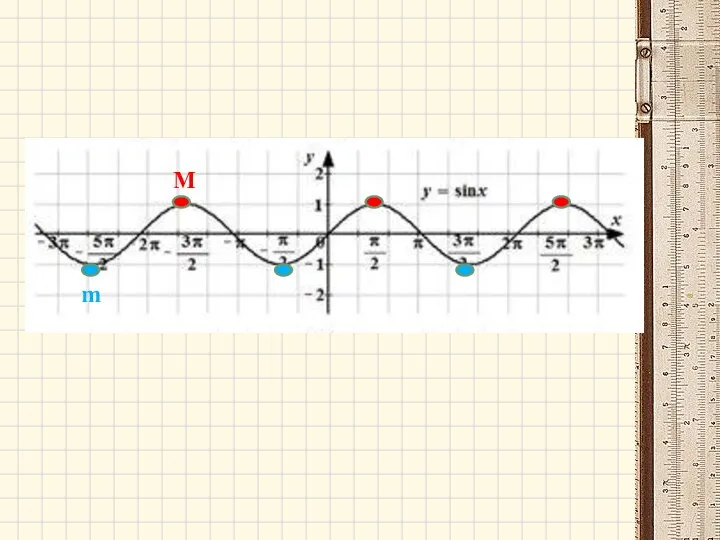
- 33. 6. Наибольшее и наименьшее значения функции Число m называют наименьшим значением функции у = f (x)
- 34. М m
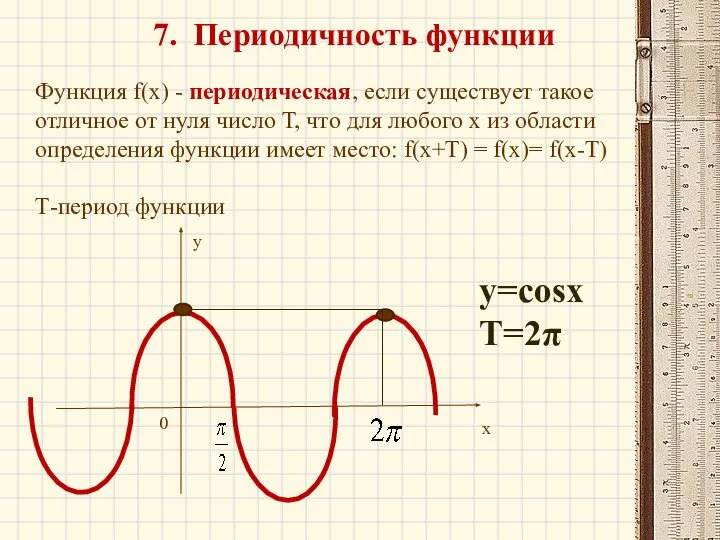
- 35. 7. Периодичность функции х у 0 Функция f(x) - периодическая, если существует такое отличное от нуля
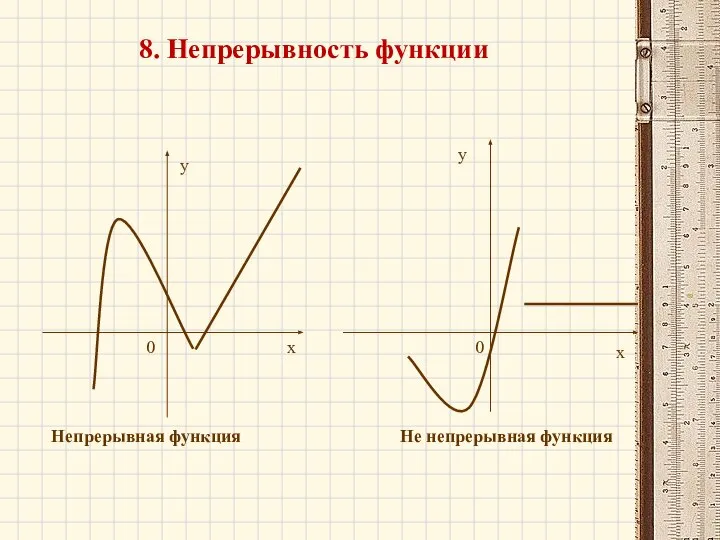
- 36. 8. Непрерывность функции х у 0 х у 0 Непрерывная функция Не непрерывная функция
- 37. 5. Обратные функции
- 38. Если функция у = f ( х ) принимает каждое своё значение у только при одном
- 39. Дано: Найти функцию, обратную данной у = f -1(x). Решение: Ответ:
- 40. х х у у 0 0 2 2 D(у)=(-∞;2)∪(2;+∞) Е(у)=(-∞;0)∪(0;+∞) 2. Е(у)=(-∞;2)∪(2;+∞) D(у)=(-∞;0)∪(0;+∞)
- 41. Свойства обратных функций Область определения обратной функции f -1 совпадает с множеством значений исходной f, а
- 42. 3. Если функция имеет обратную, то график обратной функции симметричен графику данной функции относительно прямой у
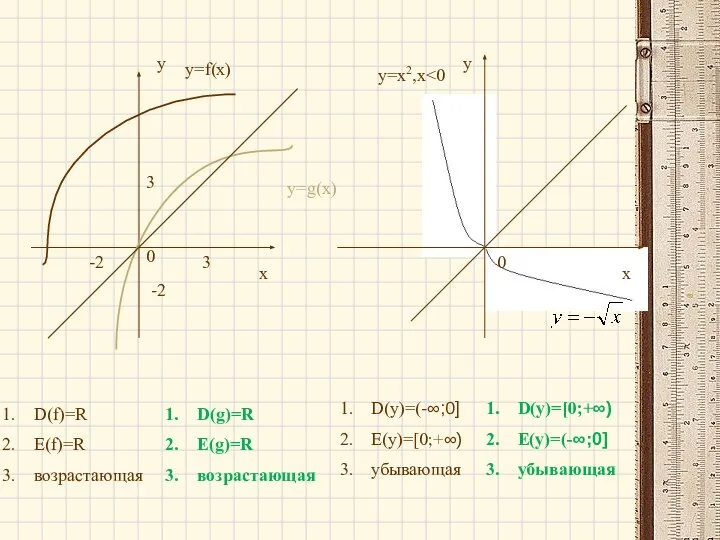
- 43. у х х у 0 0 3 3 -2 -2 у=f(x) у=g(x) y=x2,х D(f)=R E(f)=R возрастающая
- 45. Скачать презентацию








![D(y)=(-∞;+∞) E(y)=[-1;1] Период Т=2π Нечетная функция D(y)=(-∞;+∞) E(y)=[-1;1] Период Т=2π Четная функция](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1019366/slide-21.jpg)









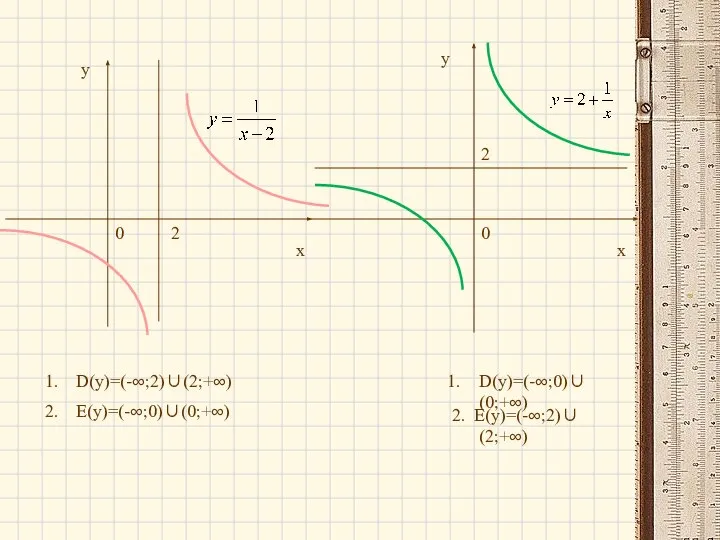


 Квадратные уравнения. Полное не приведенное и приведенное уравнения
Квадратные уравнения. Полное не приведенное и приведенное уравнения Деление десятичных дробей
Деление десятичных дробей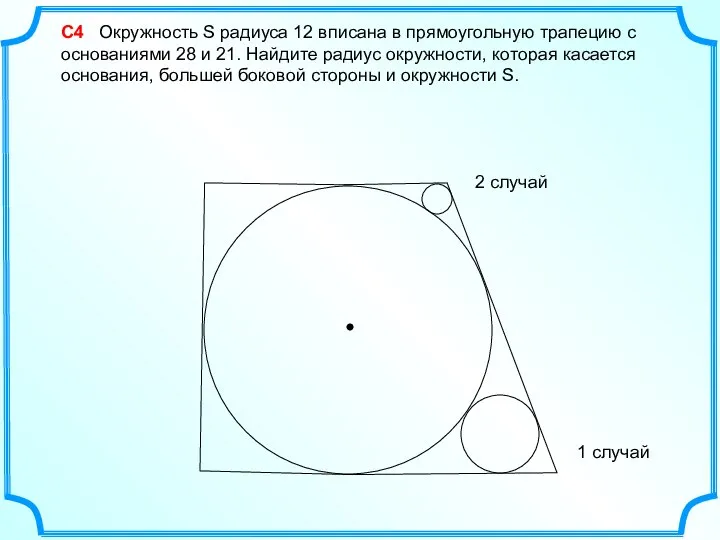 Вписанная окружность. Решение задач
Вписанная окружность. Решение задач Цилиндр
Цилиндр Решение задач с уравнением реакции
Решение задач с уравнением реакции Векторы в координатах
Векторы в координатах Векторы в пространстве
Векторы в пространстве Комбинаторика
Комбинаторика Развёртка сферы
Развёртка сферы Сфера и шар
Сфера и шар Уравнения
Уравнения Задачи с экономическим содержанием. Часть 1
Задачи с экономическим содержанием. Часть 1 Путешествие по океану МиФ Математики и Фантазии
Путешествие по океану МиФ Математики и Фантазии Переход от передаточных функций к дифференциальным уравнениям и структурным схемам
Переход от передаточных функций к дифференциальным уравнениям и структурным схемам Классификация измерений
Классификация измерений Геометрическая прогрессия
Геометрическая прогрессия Математические игры
Математические игры Решите неравенства
Решите неравенства Это полезно знать. Старинные русские меры измерения
Это полезно знать. Старинные русские меры измерения Решение уравнений. Устная работа
Решение уравнений. Устная работа Теорема о плоскости, касательной к шару
Теорема о плоскости, касательной к шару Стереометрия. Подготовка к ЕГЭ, задание В11
Стереометрия. Подготовка к ЕГЭ, задание В11 Методика изучения длины в процессе изучения геометрического материала
Методика изучения длины в процессе изучения геометрического материала Логические основы обработки информации. Алгебра логики
Логические основы обработки информации. Алгебра логики Теорема Пифагора. Решение задач
Теорема Пифагора. Решение задач Скалярное произведение векторов
Скалярное произведение векторов Системы уравнений. Основные способы их решения. 9 класс
Системы уравнений. Основные способы их решения. 9 класс Арифметические действия
Арифметические действия