- Главная
- Математика
- Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность

Содержание
- 2. Одним из способов описания нерегулярной структуры физических объектов является определение фрактальной размерности их границы Согласно Мандельброту,
- 3. Построение кривой начинается с прямолинейного отрезка единичной длины. Этот исходный отрезок может быть заменен каким-нибудь многоугольником,
- 6. Основные алгоритмы нахождения фрактальной размерности: алгоритм Ричардсона (измерение длины береговой линии) Алгоритм Ричардсона основан на измерении
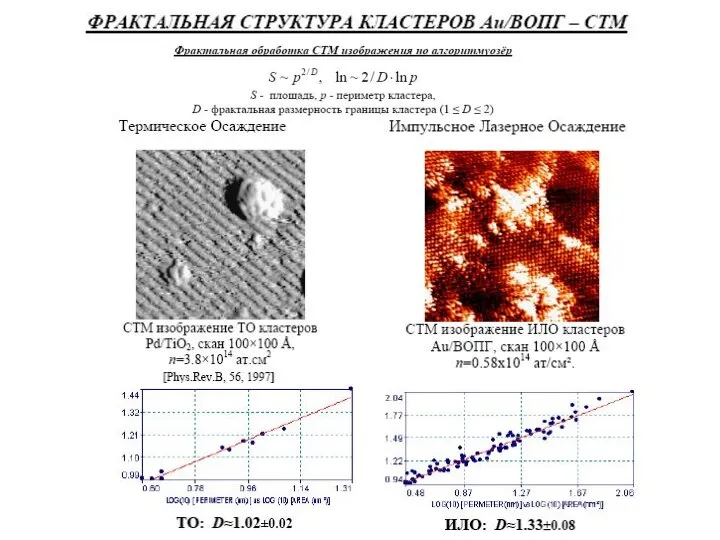
- 7. Примеры нанокластеров металла фрактальной формы В работе [Hwang R.Q., Schröder J., Günter G., Behm R.J. Fractal
- 10. Скачать презентацию
Слайд 2Одним из способов описания нерегулярной структуры физических объектов является определение фрактальной размерности
Одним из способов описания нерегулярной структуры физических объектов является определение фрактальной размерности

Согласно Мандельброту, фракталом называется структура, в которой один и тот же фрагмент повторяется при любом уменьшении масштаба. Существуют различные формулировки размерности Хаусдорфа-Безиковича, характеризующей фракталы. В частности, фрактальную размерность D множества можно определить как критическое значение показателя d в выражении меры множества Md, при котором она изменяет свое значение с нуля на бесконечность:
Мерой кривой является ее длина L, которая определяется как предел произведения числа N прямолинейных отрезков, умещающихся на кривой, на длину такого отрезка δ при ее стремлении к нулю. Для фрактальной размерности следует соотношение:
Слайд 3Построение кривой начинается с прямолинейного отрезка единичной длины. Этот исходный отрезок может
Построение кривой начинается с прямолинейного отрезка единичной длины. Этот исходный отрезок может

Кривая Коха- один из стандартных примеров фрактальной кривой.
.
Слайд 6Основные алгоритмы нахождения фрактальной размерности:
алгоритм Ричардсона (измерение длины береговой линии)
Алгоритм Ричардсона основан
Основные алгоритмы нахождения фрактальной размерности:
алгоритм Ричардсона (измерение длины береговой линии)
Алгоритм Ричардсона основан

Данный алгоритм применим для анализа изображения единичного объекта с развитой структурой границы. Поскольку впервые он был применен для измерения длины береговой линии побережья Норвегии, то он также называется алгоритмом «измерения береговой линии».
Алгоритм озер основан на определении соотношения между площадью S и периметром p исследуемого объекта. В общем случае это соотношение представляется в виде:
алгоритм озер (измерение площади и периметра объектов)
где μ(D) – величина, определяющаяся формой объекта, ν=2/D – показатель, D - фрактальная размерность границы. Построение зависимости ln(S) от ln(p) позволяет получить значение размерности исследуемых кластеров. В случае гладкой границы исследуемых объектов D=1 (S~p2). Существенным отличием данного алгоритма от алгоритма Ричардсона является то, что его невозможно использовать для определения фрактальной размерности единичного объекта.
Слайд 7Примеры нанокластеров металла фрактальной формы
В работе [Hwang R.Q., Schröder J., Günter G.,
Примеры нанокластеров металла фрактальной формы
В работе [Hwang R.Q., Schröder J., Günter G.,



 Презентация на тему Прямоугольная система координат в пространстве (11 класс)
Презентация на тему Прямоугольная система координат в пространстве (11 класс)  Задачи на построение (геометрия, 7 класс)
Задачи на построение (геометрия, 7 класс) Решение показательных уравнений
Решение показательных уравнений Теорема Пифагора
Теорема Пифагора Теорема о площади треугольника
Теорема о площади треугольника Технология подготовки учащихся к овладению функционально-графическими методами решения задач с параметрами. (Занятие №3)
Технология подготовки учащихся к овладению функционально-графическими методами решения задач с параметрами. (Занятие №3) Математический диктант
Математический диктант Среднее арифметическое
Среднее арифметическое Арифметический пейзаж
Арифметический пейзаж Задачи на концентрацию
Задачи на концентрацию Подготовка к ГИА. Задания
Подготовка к ГИА. Задания Тригонометрия. ЕГЭ, задание 7
Тригонометрия. ЕГЭ, задание 7 Геометрические фигуры
Геометрические фигуры Презентация на тему Измеряем длину окружности
Презентация на тему Измеряем длину окружности  Куб. Формулы для куба
Куб. Формулы для куба Виды четырехугольников
Виды четырехугольников Презентация на тему ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Презентация на тему ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ  Задачи на увеличение числа в несколько раз
Задачи на увеличение числа в несколько раз Проверка вычитания
Проверка вычитания Цилиндр
Цилиндр Задания по геометрии
Задания по геометрии Повторение изученного. 1 класс
Повторение изученного. 1 класс Презентация на тему Миллиметр (2 класс)
Презентация на тему Миллиметр (2 класс)  Иррациональные уравнения и их системы. Иррациональные неравенства
Иррациональные уравнения и их системы. Иррациональные неравенства Натуральные числа (5 класс)
Натуральные числа (5 класс) Prezentatsia_k_uroku_matematiki_6_klass
Prezentatsia_k_uroku_matematiki_6_klass Смешанные числа
Смешанные числа Космическая игра. Таблица умножения
Космическая игра. Таблица умножения