Теорема Гаусса-Остроградского

Пусть V – некоторая область в
пространстве, S – граница этой области.
Если функции P(x,y,z), Q(x,y,z), R(x,y,z)
непрерывны вместе со своими
частными производными во всех точках
области V, то справедлива формула:
ТЕОРЕМА.

формула
Гаусса-Остроградского
Где α, β, γ – углы, образованные внешней нормалью и осями x,y,z.

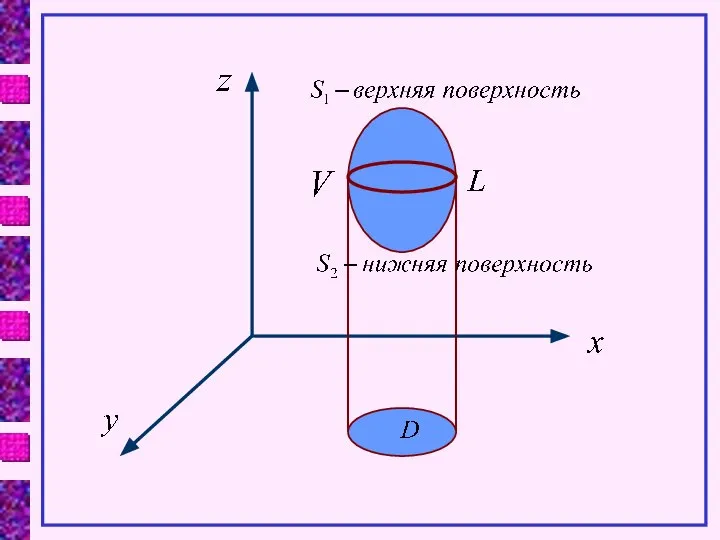
ДОКАЗАТЕЛЬСТВО:
Рассмотрим область V, ограниченную поверхностью S.
Пусть существует интеграл
Проведем цилиндрическую поверхность, проектирующую область V на плоскость ХОУ.

D – проекция областей S1 и S2 на плоскость ХОУ.
S1 : z1=z1(x,y)
S2 : z2=z2(x,y)
Сначала проинтегрируем по z:
Учтем, что

Верхняя и нижняя стороны являются внешними сторонами поверхности S, поэтому
1

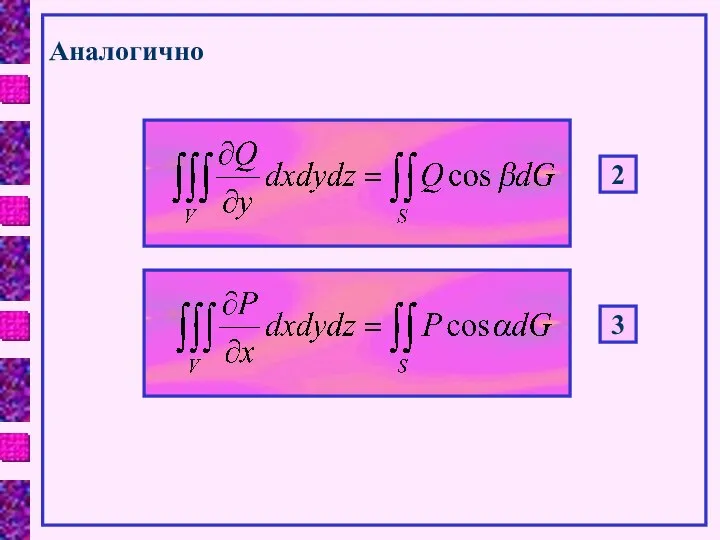
Аналогично
2
3