Задачи на нахождение элементов призмы

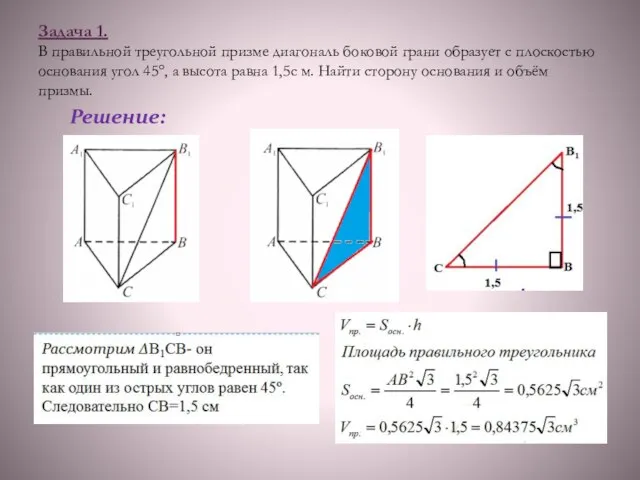
Задача 1.
В правильной треугольной призме диагональ боковой грани образует с плоскостью основания угол 45°, а высота равна 1,5 см. Найти сторону основания и объём призмы.

Как начертить прямую треугольную призму

Задача 1.
В правильной треугольной призме диагональ боковой грани образует с плоскостью основания угол 45°, а высота равна 1,5 см .Найти сторону основания и объём призмы.
ABCА1В1С1– правильная призма
∆АBC –равносторонний
В1СВ=45º
В1В=1,5 см
Дано:
Найти:
АС =?
V= ?

Задача 1.
В правильной треугольной призме диагональ боковой грани образует с плоскостью основания угол 45°, а высота равна 1,5с м. Найти сторону основания и объём призмы.
Решение:

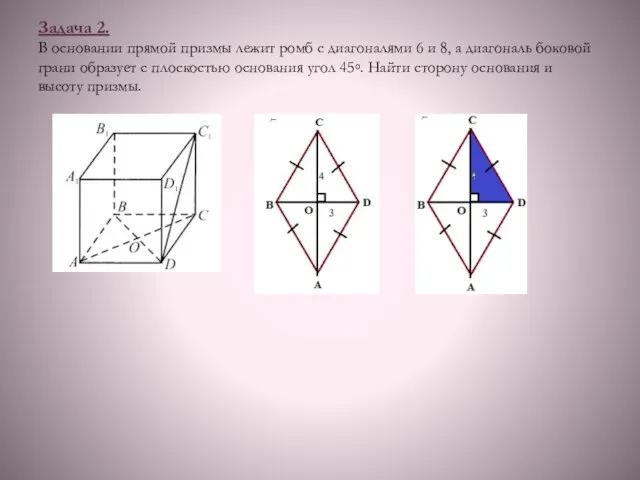
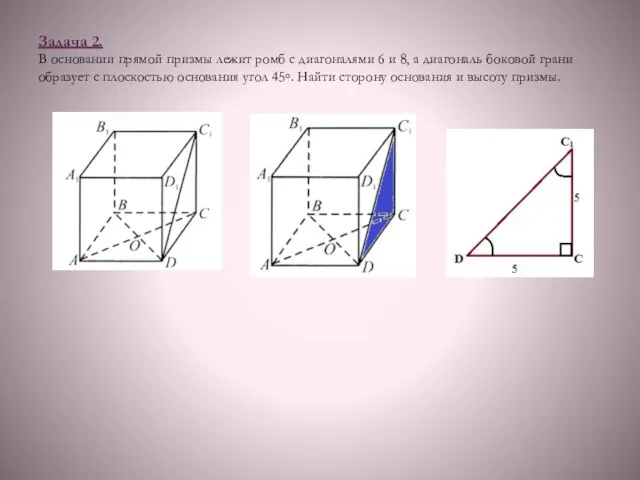
Задача 2.
В основании прямой призмы лежит ромб с диагоналями 6 и 8, а диагональ боковой грани образует с плоскостью основания угол 45◦. Найти сторону основания и высоту призмы.
Дано:
ABCDА1В1С1D1– правильная призма
АBCD –ромб
С1DC=45º
АС=8 см, ВD=6 см
Найти:
СС1=?
АВ =?

Как начертить прямую четырехугольную призму

Задача 2.
В основании прямой призмы лежит ромб с диагоналями 6 и 8, а диагональ боковой грани образует с плоскостью основания угол 45◦. Найти сторону основания и высоту призмы.

Задача 2.
В основании прямой призмы лежит ромб с диагоналями 6 и 8, а диагональ боковой грани образует с плоскостью основания угол 45◦. Найти сторону основания и высоту призмы.

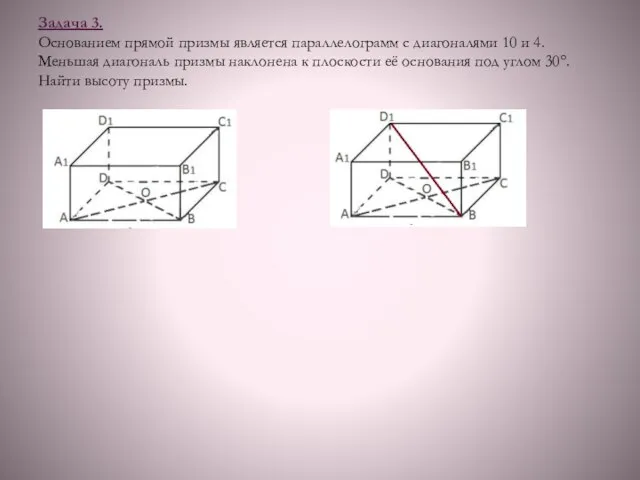
Задача 3.
Основанием прямой призмы является параллелограмм с диагоналями 10 и 4. Меньшая диагональ призмы наклонена к плоскости её основания под углом 30°. Найти высоту призмы.

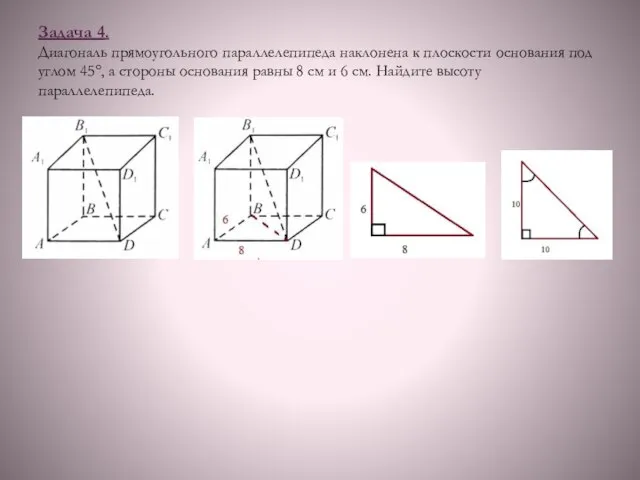
Задача 4.
Диагональ прямоугольного параллелепипеда наклонена к плоскости основания под углом 45°, а стороны основания равны 8 см и 6 см. Найдите высоту параллелепипеда.