Содержание
- 2. Функция y = x2
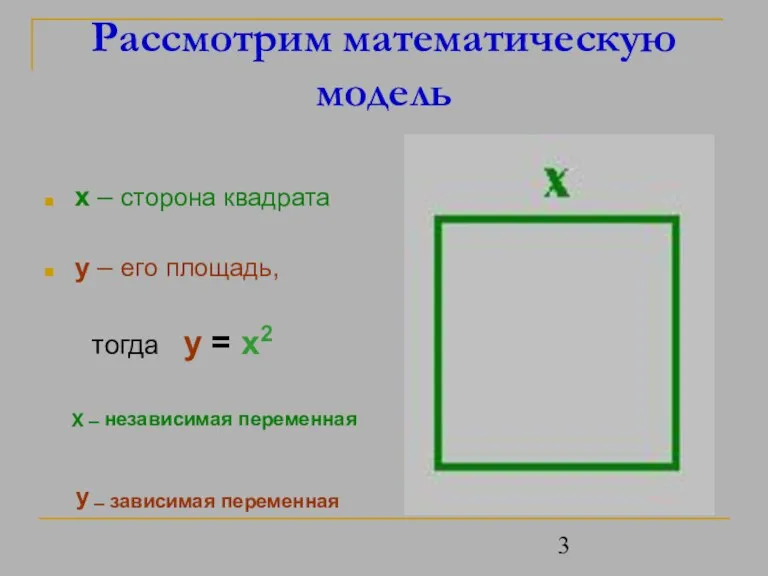
- 3. Рассмотрим математическую модель x – сторона квадрата y – его площадь, тогда y = x2 X
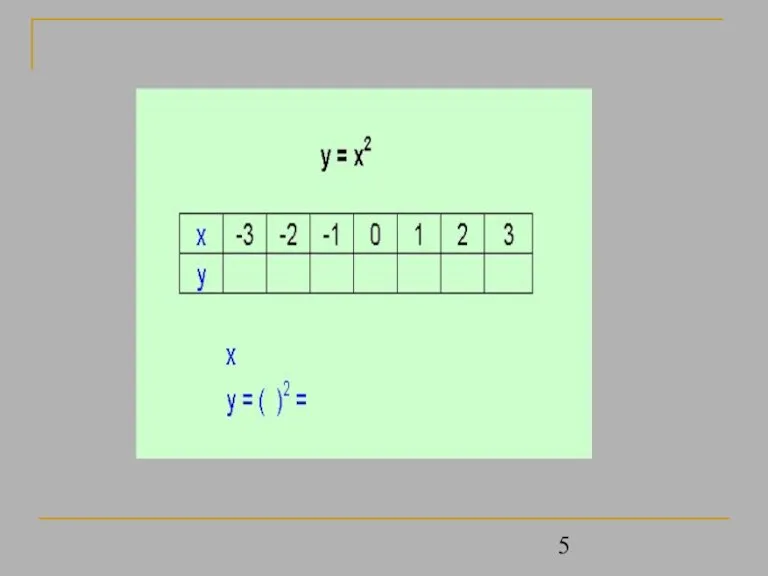
- 4. Дадим независимой переменной х конкретные значения и вычислим соответствующие значения зависимой переменной y. Рассмотрим функцию y
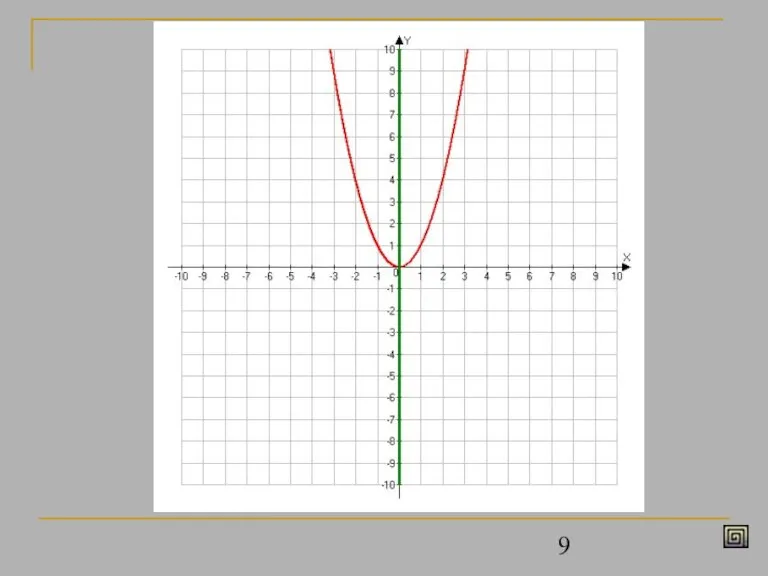
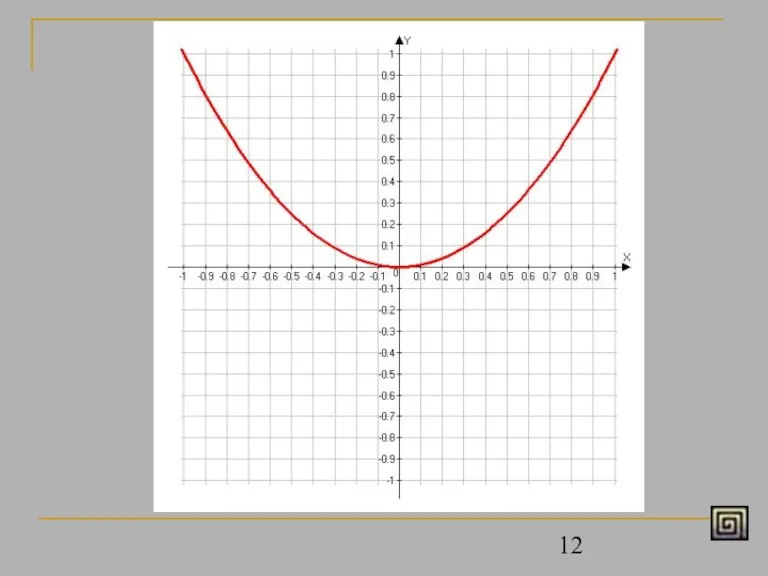
- 6. Построим график функции y = x2
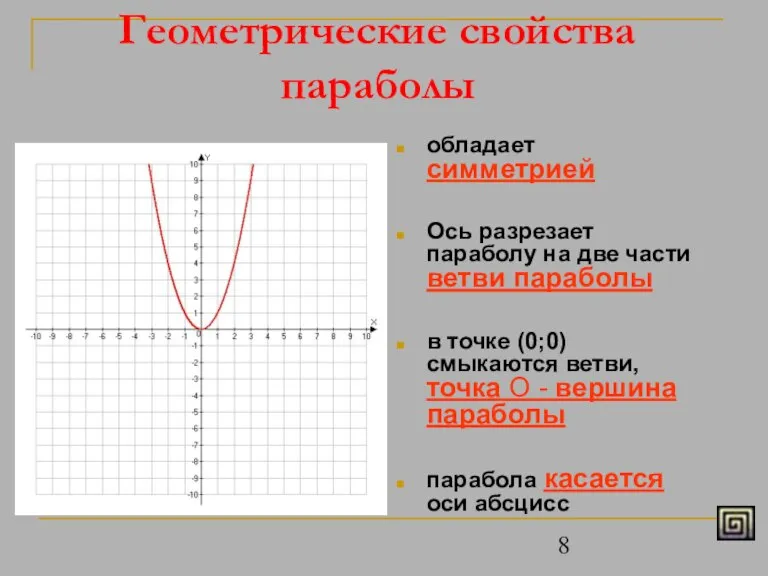
- 8. Геометрические свойства параболы обладает симметрией Ось разрезает параболу на две части ветви параболы в точке (0;0)
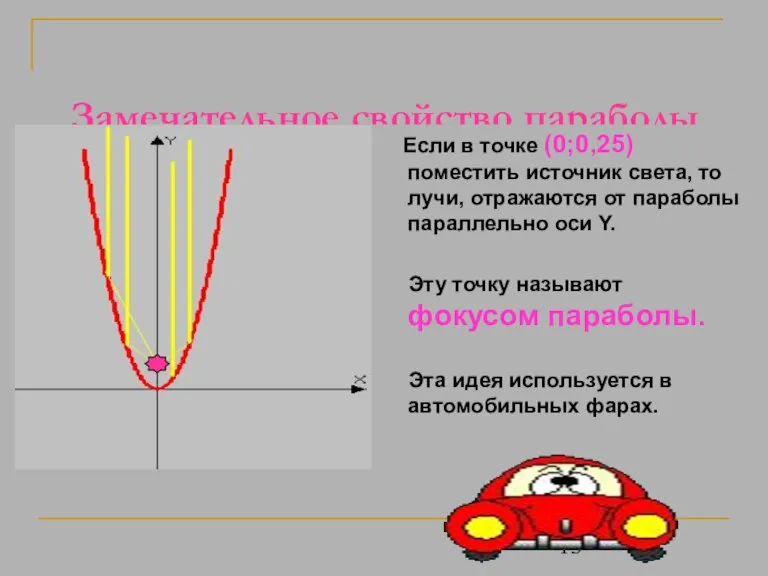
- 13. Замечательное свойство параболы Если в точке (0;0,25) поместить источник света, то лучи, отражаются от параболы параллельно
- 14. Кривые и космос Первая космическая скорость – 7,9км/c траектория – эллипс Вторая космическая скорость – 11,2км/c
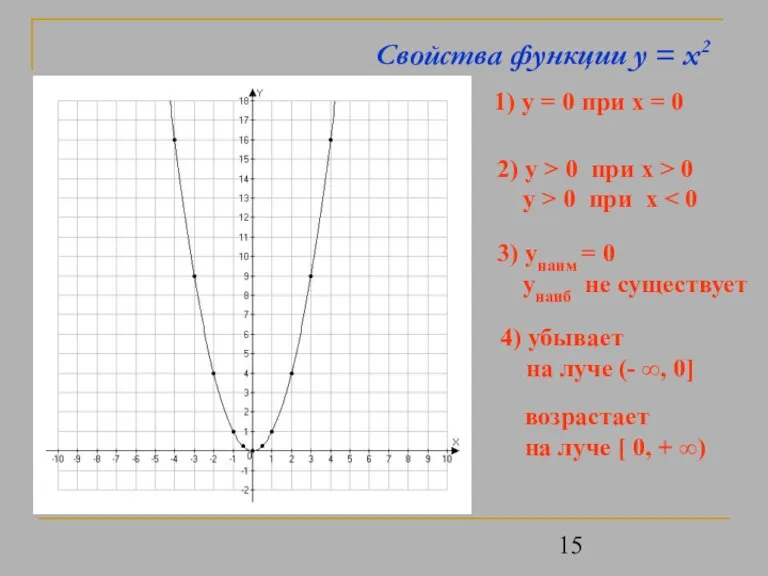
- 15. Свойства функции y = x2 1) y = 0 при x = 0 2) y >
- 16. На оси х отметим отрезок [-2 , 3] 2) Найдем на графике точки с абсциссами -2
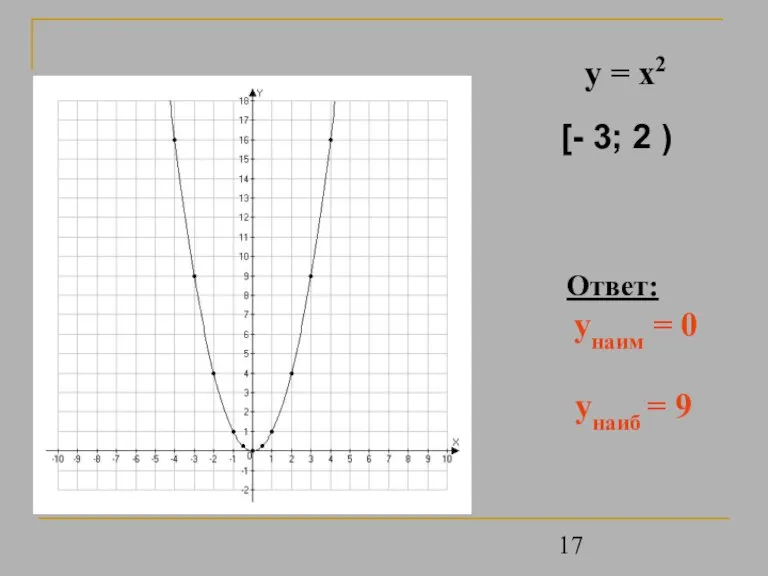
- 17. Ответ: унаим = 0 унаиб = 9 y = x2 [- 3; 2 )
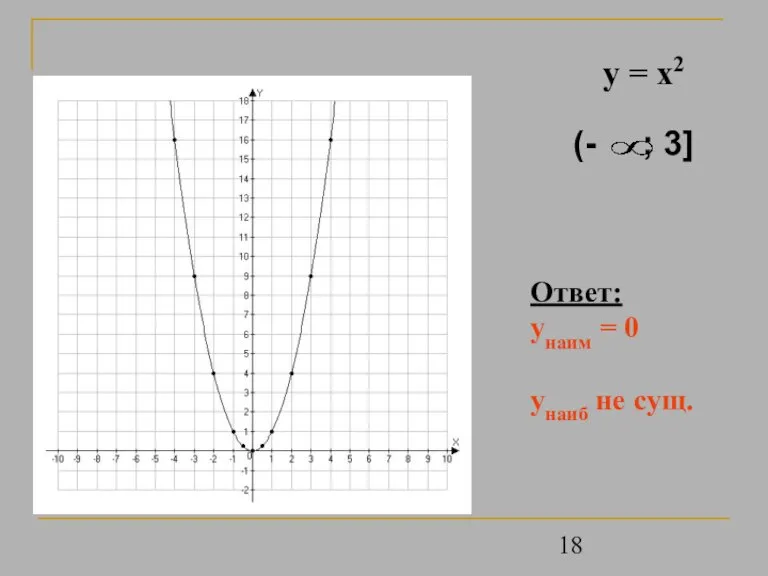
- 18. y = x2 Ответ: унаим = 0 унаиб не сущ.
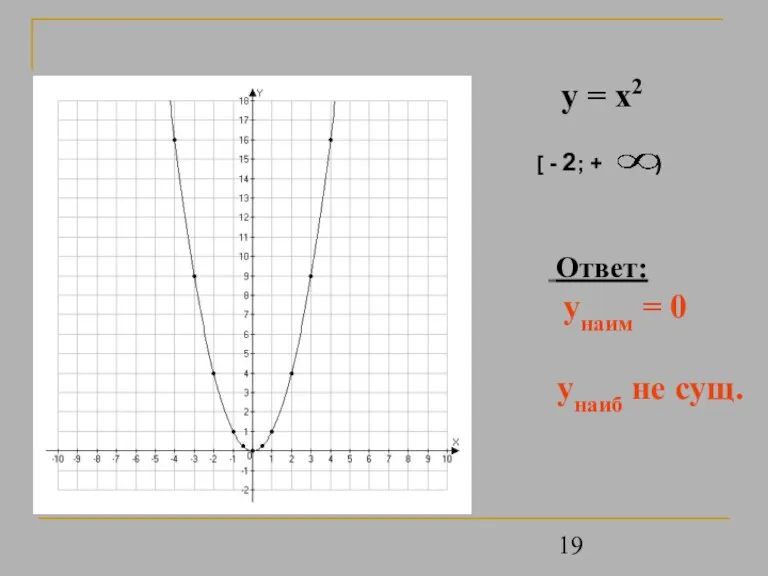
- 19. y = x2 Ответ: унаим = 0 унаиб не сущ.
- 20. Ответ: унаим = 1 унаиб = 9 y = x2 [ 1; 3]
- 21. y = x2 Ответ: унаим = 1 унаиб = 9 [- 3; - 1]
- 22. Использованные ресурсы http://gif.10000.ru/archiv/main.asp?RubricID=55&First=1&Last=5 http://www.km.ru/ http://www.1 september.ru/ http://math.ournet.md/indexr.html Мордкович А.Г. Алгебра. 7 кл. В 2 ч.: Ч.1:
- 24. Скачать презентацию





![На оси х отметим отрезок [-2 , 3] 2) Найдем на графике](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/338105/slide-15.jpg)
![Ответ: унаим = 1 унаиб = 9 y = x2 [ 1; 3]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/338105/slide-19.jpg)
![y = x2 Ответ: унаим = 1 унаиб = 9 [- 3; - 1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/338105/slide-20.jpg)

 Презентация на тему Даниил Заточник
Презентация на тему Даниил Заточник Pervoobraznaya.ppt
Pervoobraznaya.ppt Методы решения квадратного уравнения
Методы решения квадратного уравнения Действия над обыкновенными дробями
Действия над обыкновенными дробями Применение неравенств и их свойств
Применение неравенств и их свойств Дробные рациональные уравнения
Дробные рациональные уравнения Lineynye-uravneniya-s-odnoy-peremennoy.pptx
Lineynye-uravneniya-s-odnoy-peremennoy.pptx Прогрессия - движение вперёд !
Прогрессия - движение вперёд ! Неравенства и их решения
Неравенства и их решения  Элементы математической статистики
Элементы математической статистики Презентация на тему Основные закономерности развития науки
Презентация на тему Основные закономерности развития науки  Презентация на тему ДЖОРДАНО БРУНО
Презентация на тему ДЖОРДАНО БРУНО  Алгебра модуля
Алгебра модуля Приём вычислений вида 26+4 Математика 2 класс
Приём вычислений вида 26+4 Математика 2 класс 9-klass-kvadratichnaya-funkciya.ppt
9-klass-kvadratichnaya-funkciya.ppt Применение производной к исследованию функции
Применение производной к исследованию функции Приращение аргумента. Приращение функции
Приращение аргумента. Приращение функции Неравенства с двумя переменными
Неравенства с двумя переменными Презентация на тему Место муниципального права в российском праве
Презентация на тему Место муниципального права в российском праве  Многочлены
Многочлены Презентация на тему Понятие и предмет международного частного права
Презентация на тему Понятие и предмет международного частного права  Квадратное уравнение Ладанова И.В. МКОУ «Верх-Жилинская ООШ»
Квадратное уравнение Ладанова И.В. МКОУ «Верх-Жилинская ООШ»  Эпоха Просвещения в России
Эпоха Просвещения в России Прямая пропорциональная зависимость
Прямая пропорциональная зависимость Понятие обратной функции. Определение логарифмической функции
Понятие обратной функции. Определение логарифмической функции Пропорция
Пропорция Определение производной функции y=f(x) в точке
Определение производной функции y=f(x) в точке Презентация на тему Позиции критиков норманской теории
Презентация на тему Позиции критиков норманской теории