Содержание
- 2. методы Метод касательных Метод половинногоМетод половинного деления Метод хорд Метод комбинированный Метод итераций
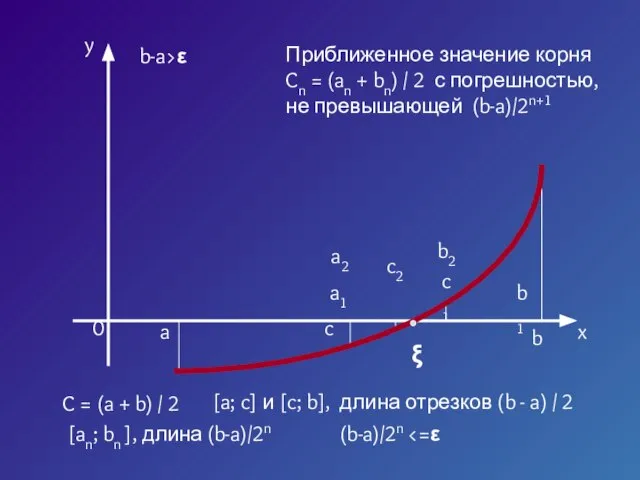
- 3. Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём b – a >
- 4. x y a b c C = (a + b) / 2 a1 b1 c1 a2
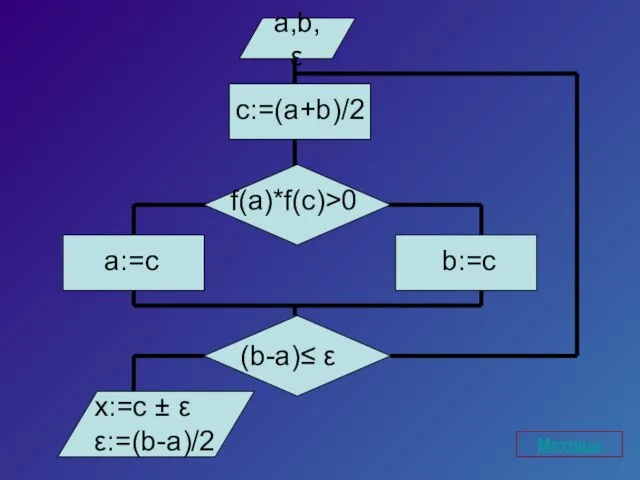
- 5. a,b, ε f(a)*f(c)>0 a:=c x:=c ± ε ε:=(b-a)/2 c:=(a+b)/2 b:=c (b-a)≤ ε Методы
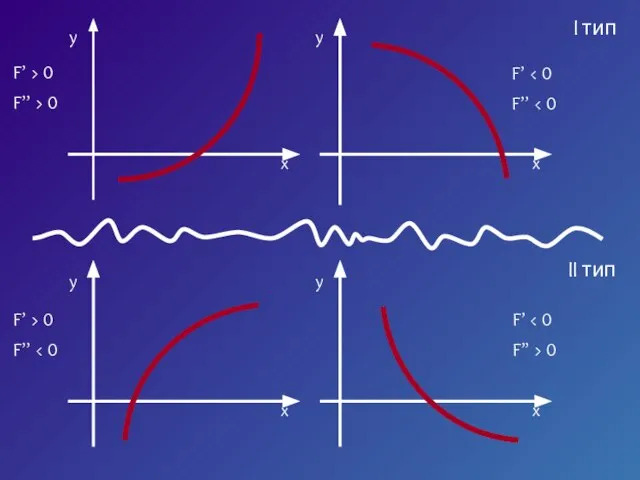
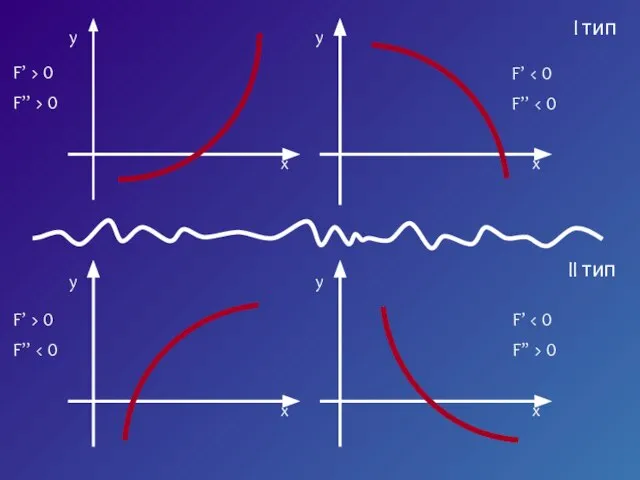
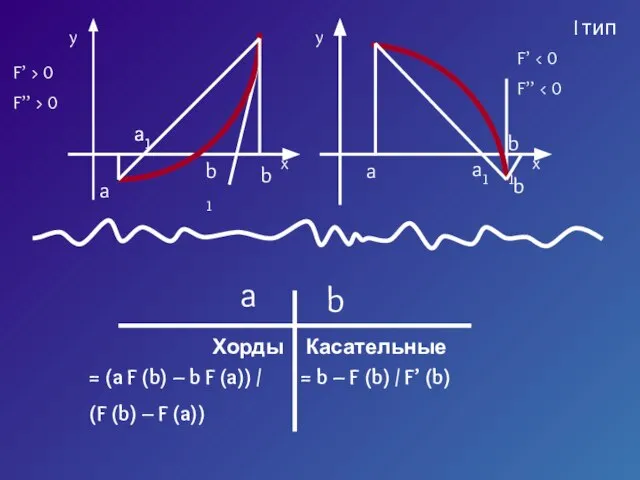
- 6. I тип II тип
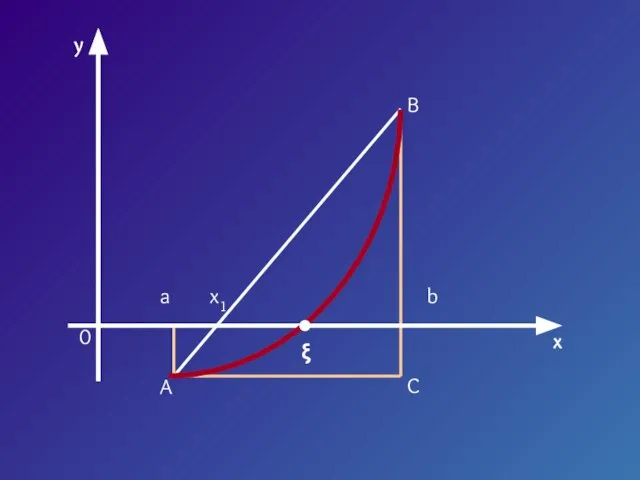
- 7. Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать: F (x)
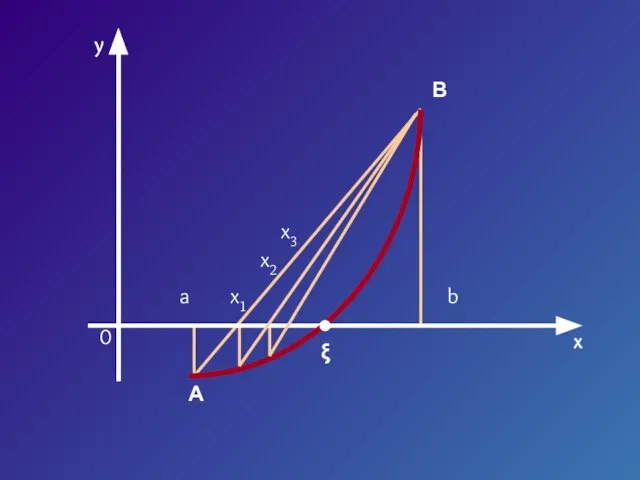
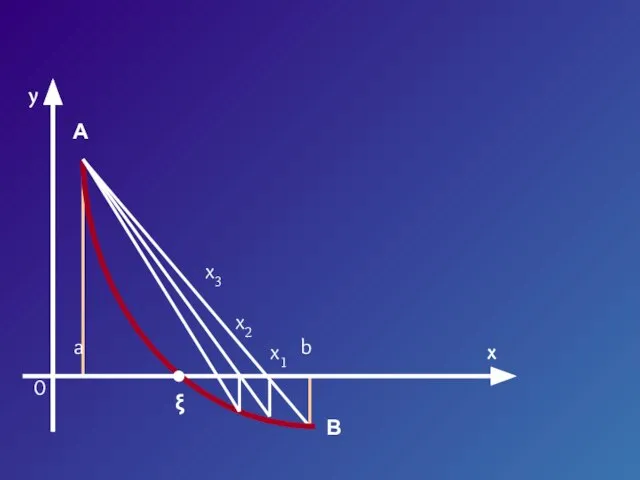
- 8. y x 0 a b x1 x2 x3 ξ A B
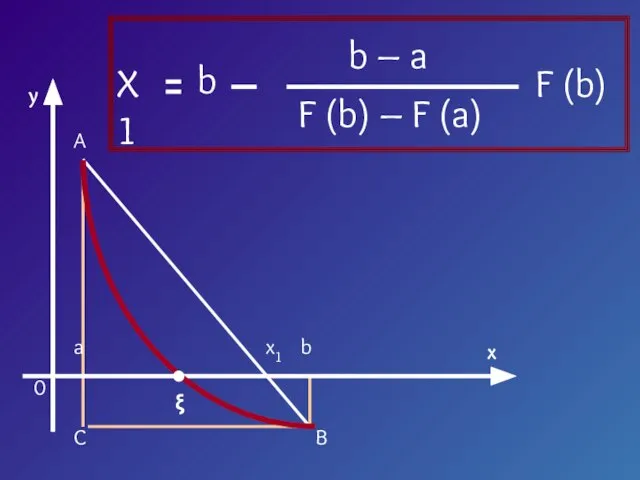
- 9. y x 0 a b x1 ξ A C B
- 10. Треугольник AaX1 подобен треугольнику ABC X1 – a F (a) b – a F (a) –
- 12. y x 0 a b x2 ξ x1 x3 A B
- 13. y x 0 a b x1 ξ A C B
- 14. Методы
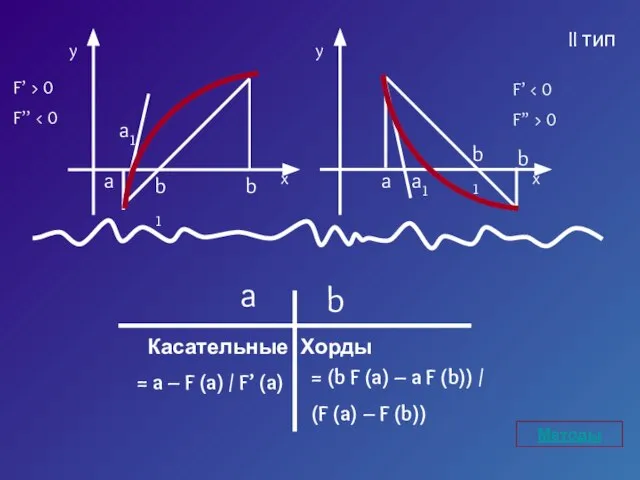
- 15. I тип II тип
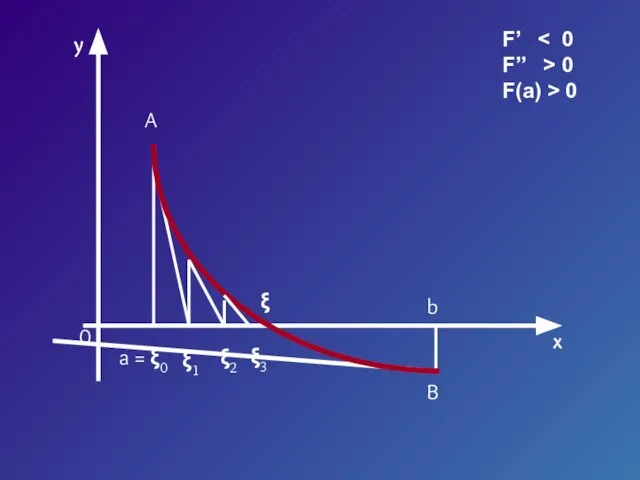
- 16. Пусть корень ξ уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать: F
- 17. y x 0 a = ξ0 b ξ1 ξ2 A B F’ F’’ > 0 F(a)
- 18. Уравнение касательной в точке A (a, F (a)) : y – F (a) = F’ (a)*(x
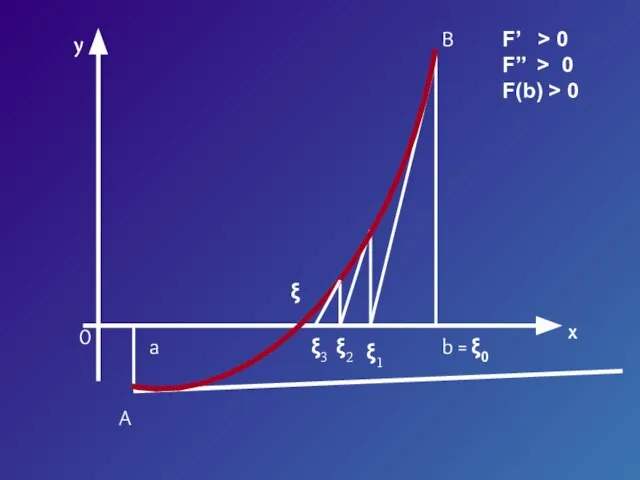
- 19. y x 0 a b = ξ0 ξ1 ξ2 A B F’ > 0 F’’ >
- 20. Если касательную к кривой провести в точке B (в правом конце), то получим
- 21. Методы x0 = a II тип x0 = b I тип
- 22. I тип Хорды b a Касательные = (a F (b) – b F (a)) / (F
- 23. II тип Хорды b a Касательные = (b F (a) – a F (b)) / (F
- 27. Скачать презентацию

![Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/304492/slide-2.jpg)
![Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/304492/slide-6.jpg)

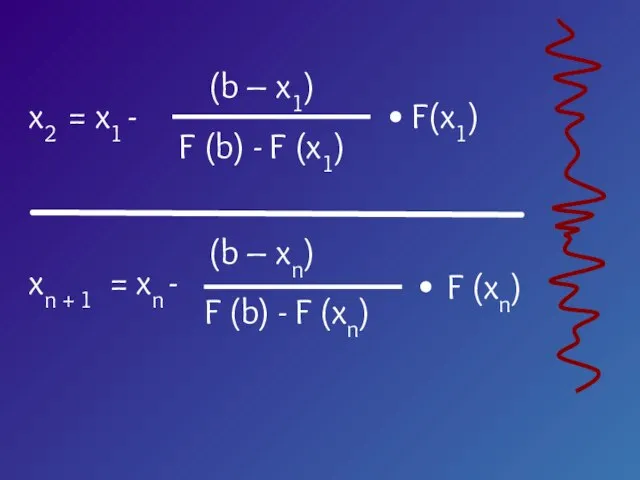




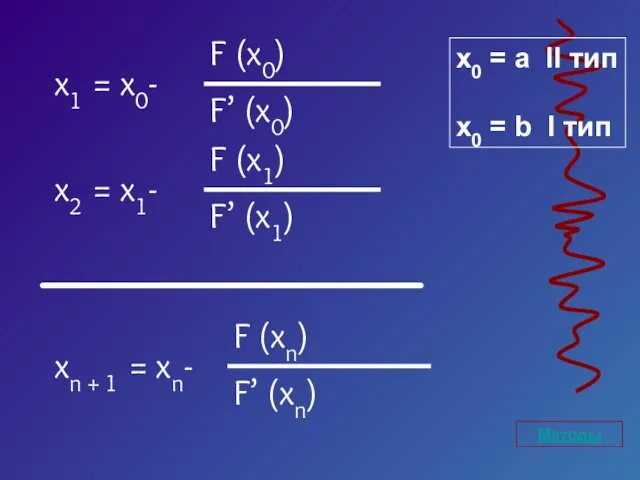


 Математическая статистика в жизни класса
Математическая статистика в жизни класса Презентация на тему Глубинная психология
Презентация на тему Глубинная психология  Производная и ее применение (10 класс)
Производная и ее применение (10 класс) Первообразная
Первообразная Урок в 11 классе. Урок в 11 классе. Составила учитель Кировской МБОУ Ткачук Н. П.
Урок в 11 классе. Урок в 11 классе. Составила учитель Кировской МБОУ Ткачук Н. П.  Наглядное представление статистической информации
Наглядное представление статистической информации Презентация на тему Состояние правового регулирования экологических прав граждан и общественных организаций по российскому зако
Презентация на тему Состояние правового регулирования экологических прав граждан и общественных организаций по российскому зако Урок алгебры в 7 классе Тема: «Разность квадратов»
Урок алгебры в 7 классе Тема: «Разность квадратов»  Презентация на тему Механистическая картина мира
Презентация на тему Механистическая картина мира  Решение неравенств с одной переменной Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная шко
Решение неравенств с одной переменной Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная шко МОУ «Аминевская СОШ» А.Н. Ямалетдинова- учитель математики.
МОУ «Аминевская СОШ» А.Н. Ямалетдинова- учитель математики. Презентация на тему ТЕСТ «Логистика
Презентация на тему ТЕСТ «Логистика  Алгебра и начала анализа
Алгебра и начала анализа Квадратные уравнения и уравнения, приводимые к квадратным
Квадратные уравнения и уравнения, приводимые к квадратным «Применение производной для исследования функции»
«Применение производной для исследования функции»  Комбинаторика Правило сложения Правило умножения
Комбинаторика Правило сложения Правило умножения Алгебраические дроби (8 класс)
Алгебраические дроби (8 класс) Презентация на тему Тест на самопроверку знаний
Презентация на тему Тест на самопроверку знаний  Свойства функции У = sin x и ее график
Свойства функции У = sin x и ее график Обобщающий урок по теме: «Решение неравенств с одной переменной и решение систем неравенств»
Обобщающий урок по теме: «Решение неравенств с одной переменной и решение систем неравенств» ГИА 2013 Модуль «Реальная математика» №17
ГИА 2013 Модуль «Реальная математика» №17 Линейные уравнения ax=b
Линейные уравнения ax=b ааапмп
ааапмп Toplivno-energeticheskii_774_komplex_Rossii_9_klass_Prezentatsia_k_otkrytomu_uroku.pptx
Toplivno-energeticheskii_774_komplex_Rossii_9_klass_Prezentatsia_k_otkrytomu_uroku.pptx Основные понятия, связанные с квадратными уравнениями
Основные понятия, связанные с квадратными уравнениями Что такое функция 7 класс
Что такое функция 7 класс Решение квадратных уравнений по формуле
Решение квадратных уравнений по формуле 667
667