Решение уравнений и неравенств, содержащих модуль, методом интервалов

Модулем действительного числа а ( |а| ) называется:
само это число, если а – положительное число;
нуль, если число а – нуль;
число, противоположное а , если число а – отрицательное.
Или
а, если а>0
0, если а=0
-а, если а<0
|а| =
Определение модуля

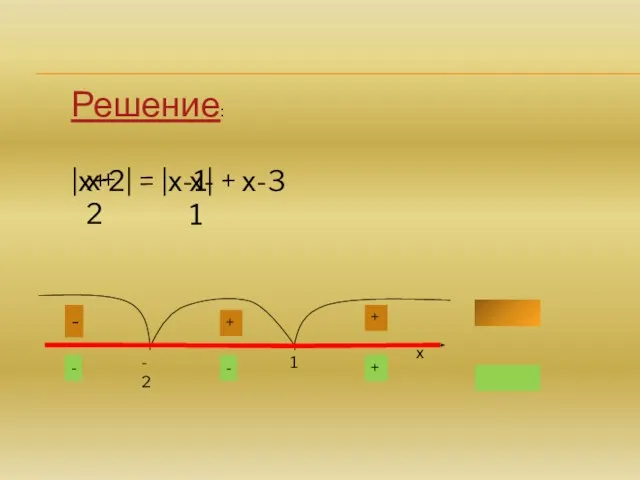
№ 1. Решить уравнение:
|х+2| = |х-1| + х-3

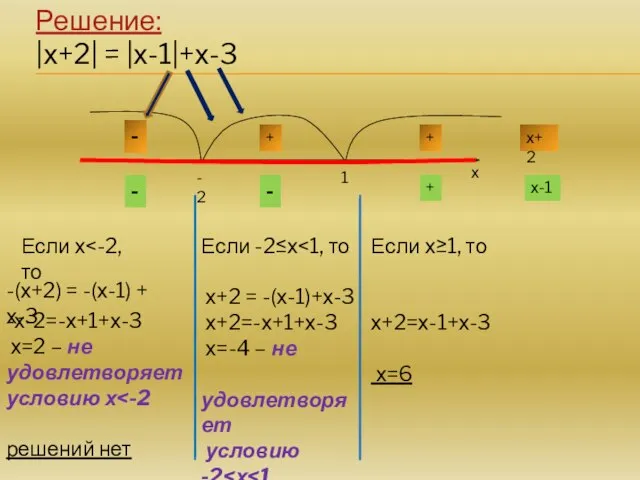
Решение:
|х+2| = |х-1| + х-3
=0 при х=-2
=0 при х=1
х+2
х-1
-2
1

Решение:
|х+2| = |х-1| + х-3
-2
1
х
х+2
х-1
-
-
+
-
+
+

Решение:
|х+2| = |х-1|+х-3
х
-х-2=-х+1+х-3
х=2 – не удовлетворяет
условию х<-2
решений нет
Если -2≤х<1, то
х+2 = -(х-1)+х-3
х+2=-х+1+х-3
х=-4 – не
удовлетворяет
условию -2<х<1
решений нет
Если х≥1, то
х+2=х-1+х-3
х=6
Если х<-2, то
-(х+2) = -(х-1) + х-3

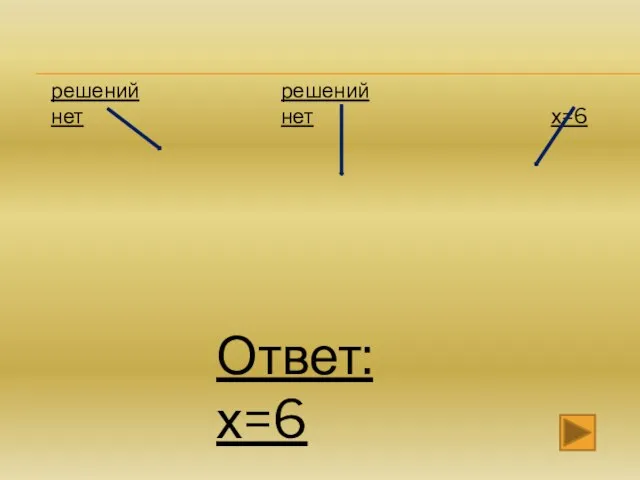
решений нет
решений нет
х=6
Ответ: х=6

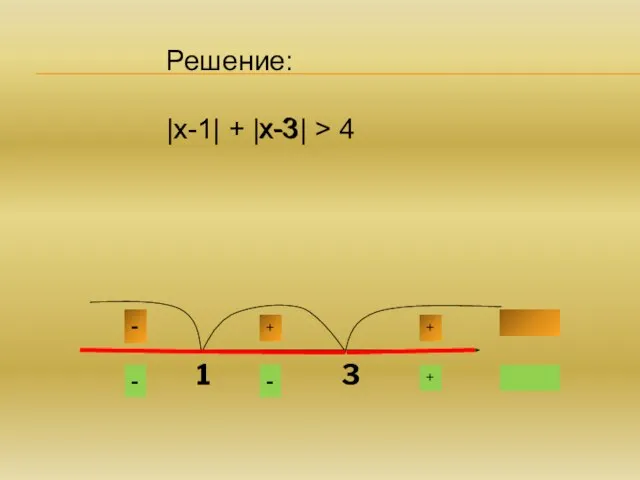
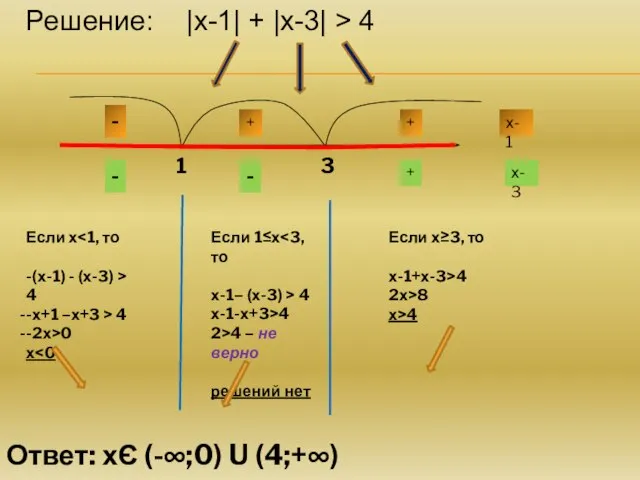
№2. Решить неравенство:
|х-1| + |х-3| > 4

Решение:
|х-1| + |х-3| > 4
х-1
х-3
= 0 при х=1
=0 при х=3
1
3

-
+
+
+
-
-
Решение:
|х-1| + |х-3| > 4
х-1
х-3

Решение: |х-1| + |х-3| > 4
Если х<1, то
-(х-1) - (х-3) > 4
-х+1 –х+3 > 4
-2х>0
х<0
Если 1≤х<3, то
х-1– (х-3) > 4
х-1-х+3>4
2>4 – не верно
решений нет
Если х≥3, то
х-1+х-3>4
2х>8
х>4
Ответ: хЄ (-∞;0) U (4;+∞)

Общий алгоритм
найти нули подмодульных выражений и отметить их на числовой прямой
определить знаки подмодульных выражений на полученных промежутках
на каждом промежутке решить уравнение ( неравенство )
объединить полученные решения

Большое количество ошибок при решении задач с модулями вызвано тем, что многие, освобождаясь от модуля, забывают учесть условия, при которых модуль был раскрыт с тем или иным знаком.

Поэтому при решении задач, в которые входят два или более модулей, рекомендуется использовать метод интервалов.