Геометрия.Введение. Аксиоматика.

IV – V вв. до н.э. – ПИФАГОРЕЙСКАЯ ШКОЛА
ПЕНТОГРАММА

М е ф и с т о ф е л ь:
Нет, трудновато выйти мне теперь
Тут кое-что мешает мне немного:
Волшебный знак у вашего порога.
Ф а у с т:
Не пентаграмма ль этому виной?
Но как же, бес, пробрался ты за мной?
Каким путем впросак попался?
М е ф и с т о ф е л ь:
Изволили ее вы плохо начертить,
И промежуток в уголку остался,
Там, у дверей, –
и я свободно мог вскочить.
Ф а у с т. Г е т е.

Египетский

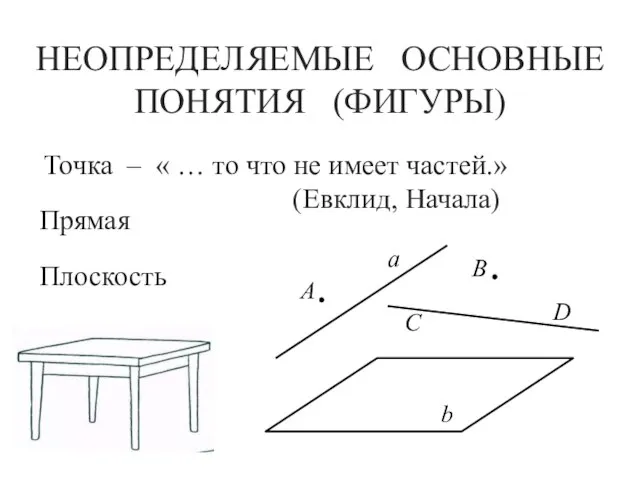
НЕОПРЕДЕЛЯЕМЫЕ ОСНОВНЫЕ ПОНЯТИЯ (ФИГУРЫ)
Точка – « … то что не имеет частей.» (Евклид, Начала)
Прямая
Плоскость
а
А
В
D
С
b

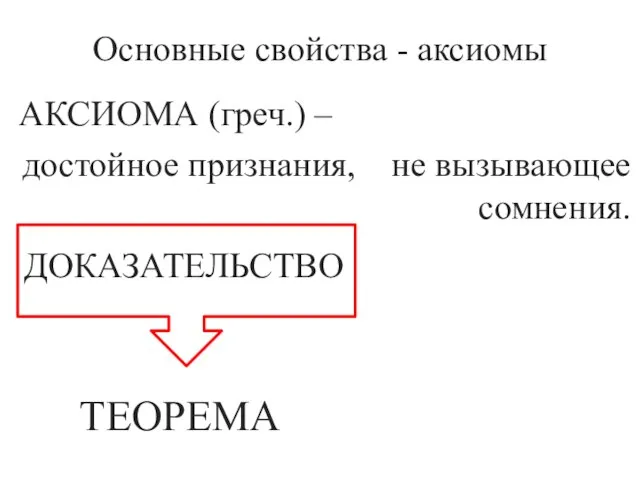
АКСИОМА (греч.) –
достойное признания, не вызывающее сомнения.
Основные свойства - аксиомы
ДОКАЗАТЕЛЬСТВО
ТЕОРЕМА

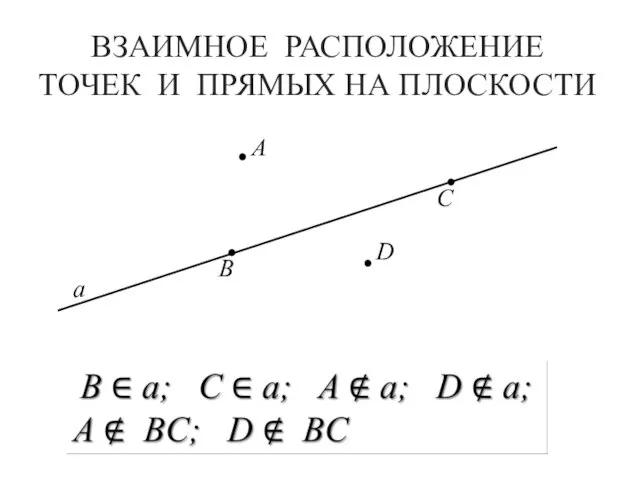
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ
А
B
C
D
а

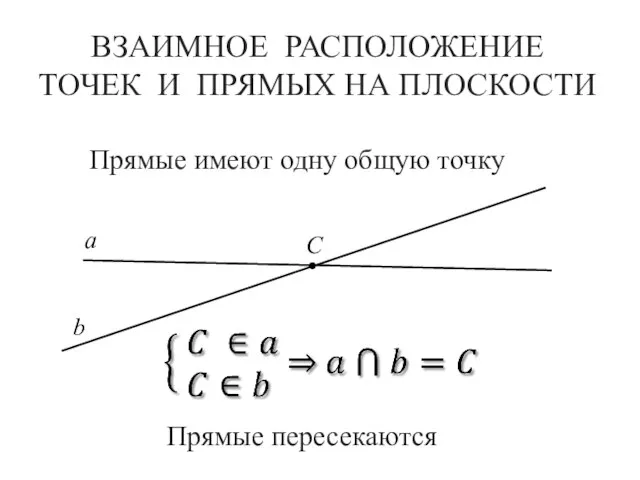
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ
а
b
C
Прямые пересекаются
Прямые имеют одну общую точку

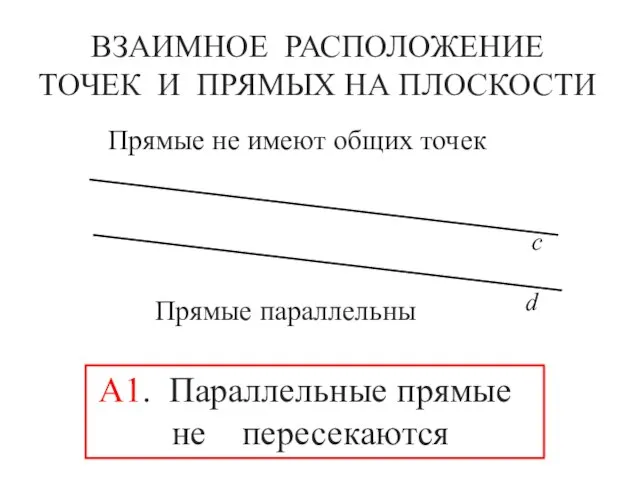
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ
с
d
Прямые не имеют общих точек
Прямые параллельны А1. Параллельные прямые
не пересекаются

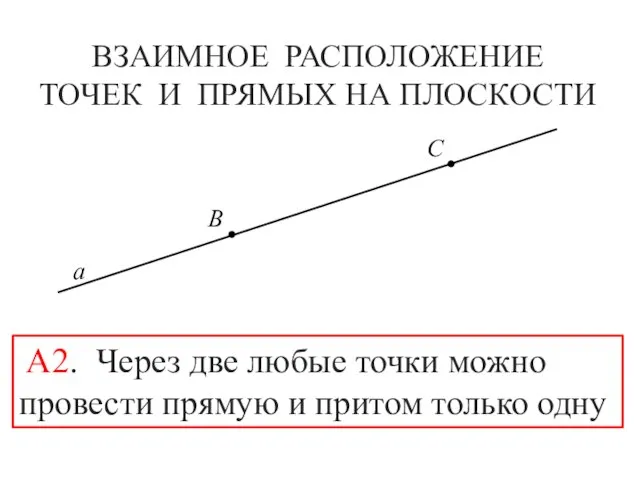
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ
B
C
а
А2. Через две любые точки можно провести прямую и притом только одну

Провести четыре прямые так чтобы каждые две из них пересекались, но никакие три не пересекались в одной точке.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ
Сколько прямых изображено?
Сколько у них точек попарных пересечений? Обозначьте.

Сколько прямых можно провести через
а) три точки
б) четыре точки
Рассмотрите все возможные случаи.
Выполните построения.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ