Содержание
- 2. ВСПОМНИТЕ ОТВЕТЫ НА ВОПРОСЫ 1) Сформулируй понятие площади геометрической фигуры. 2) Сформулируй основные свойства площадей геометрических
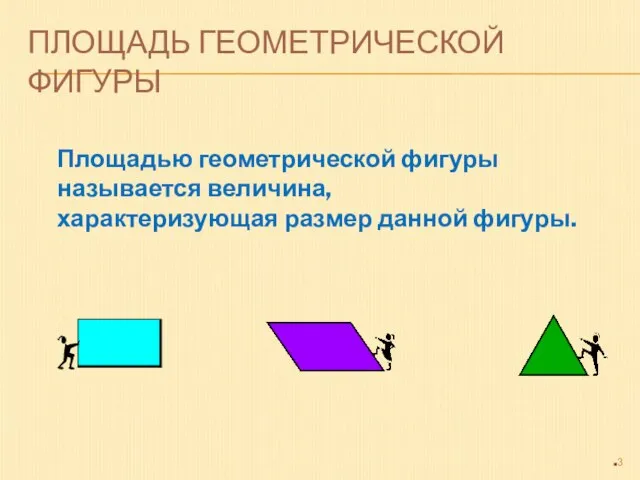
- 3. ПЛОЩАДЬ ГЕОМЕТРИЧЕСКОЙ ФИГУРЫ Площадью геометрической фигуры называется величина, характеризующая размер данной фигуры.
- 4. ОСНОВНЫЕ СВОЙСТВА ПЛОЩАДЕЙ ГЕОМЕТРИЧЕСКИХ ФИГУР - Любая плоская геометрическая фигура имеет площадь. - Эта площадь –
- 5. ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА Площадь прямоугольника равна произведению двух его соседних сторон. в S = а · в
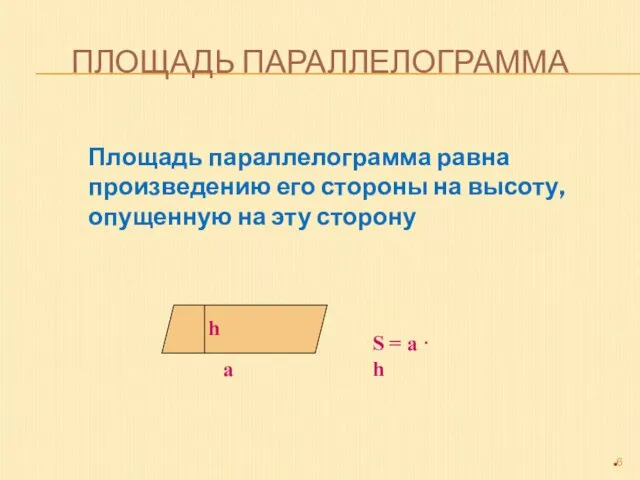
- 6. ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА Площадь параллелограмма равна произведению его стороны на высоту, опущенную на эту сторону а S
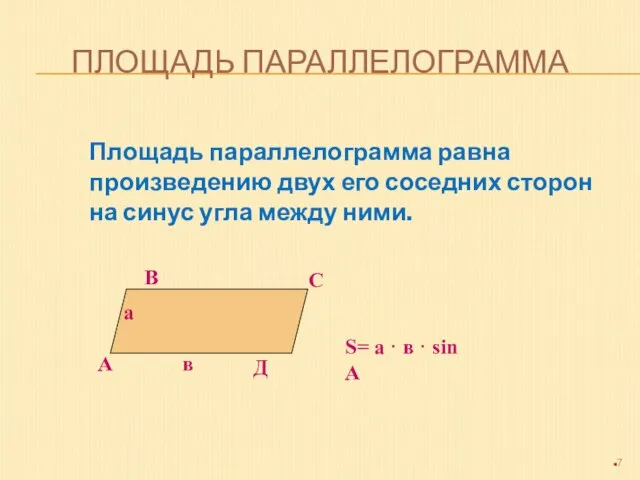
- 7. ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними. а
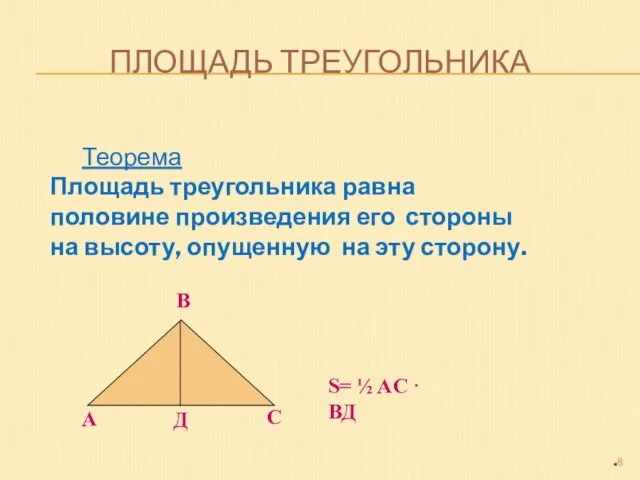
- 8. ПЛОЩАДЬ ТРЕУГОЛЬНИКА Теорема Площадь треугольника равна половине произведения его стороны на высоту, опущенную на эту сторону.
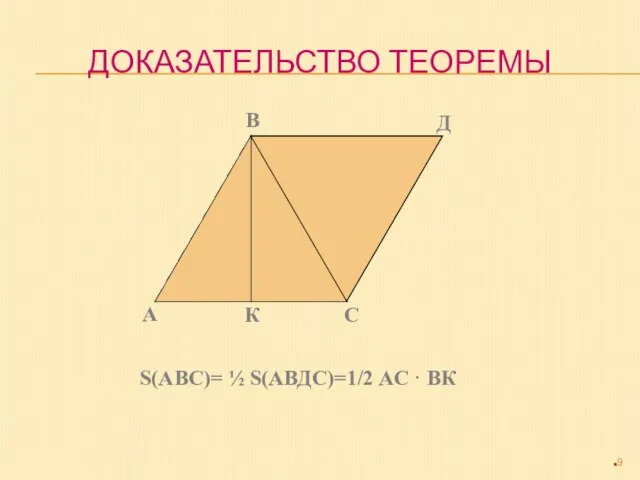
- 9. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ А В Д С К S(АВС)= ½ S(АВДС)=1/2 АС · ВК
- 10. СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ Попробуй доказать самостоятельно следующие следствия из теоремы:
- 11. СЛЕДСТВИЕ 1 Площадь прямоугольного треугольника равна половине произведения его катетов. А В С S= ½ ВС
- 12. СЛЕДСТВИЕ 2 Площадь тупоугольного треугольника равна произведению любой из его сторон на высоту, опущенную на прямую,
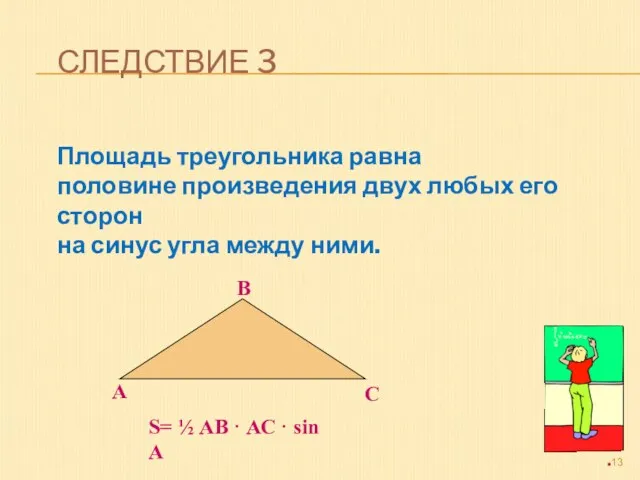
- 13. СЛЕДСТВИЕ 3 Площадь треугольника равна половине произведения двух любых его сторон на синус угла между ними.
- 14. СЛЕДСТВИЕ 4 Площадь равностороннего треугольника вычисляется по формуле: где а – сторона треугольника
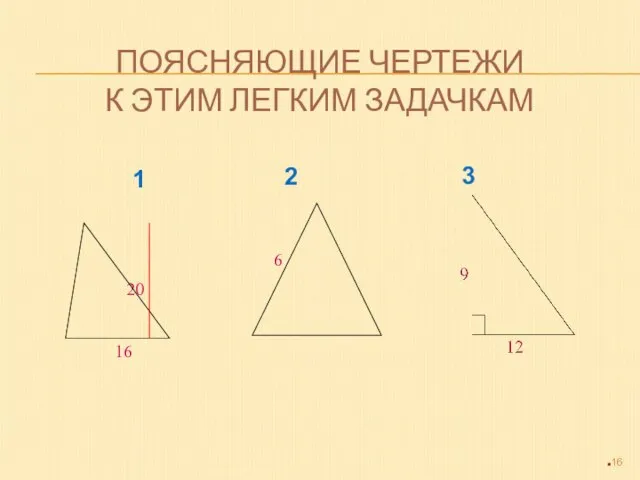
- 15. СНАЧАЛА РЕШИ ЛЕГКИЕ ЗАДАЧКИ 1. Найти площадь треугольника, основание которого равно 16 см, а высота, опущенная
- 16. ПОЯСНЯЮЩИЕ ЧЕРТЕЖИ К ЭТИМ ЛЕГКИМ ЗАДАЧКАМ 1 2 3
- 17. ТЕПЕРЬ РЕШИ ЗАДАЧКИ ПОТРУДНЕЕ 1. В равнобедренном треугольнике боковая сторона равна 13 см, а основание равно
- 18. ТЕПЕРЬ РЕШИ САМЫЕ ТРУДНЫЕ ЗАДАЧИ 1. Боковая сторона равнобедренного треугольника равна a, а угол при основании
- 19. ОТВЕТЫ К ЛЕГКИМ ЗАДАЧКАМ 1. 160 см2 2. 9 см 2 3. 54 см 2
- 20. ОТВЕТЫ К БОЛЕЕ ТРУДНЫМ ЗАДАЧКАМ 1. 60 см 2 2. 3. 24 см 2
- 21. ОТВЕТЫ К САМЫМ ТРУДНЫМ ЗАДАЧКАМ 1. ½ a2sin2α 2. 3.
- 22. ЭТО ИНТЕРЕСНО! Определение площадей геометрических фигур - одна из древнейших практических задач. Правильный подход к их
- 23. Например, мы уже знаем, как можно вычислить площадь квадрата, прямоугольника и параллелограмма, а нам нужно вычислить
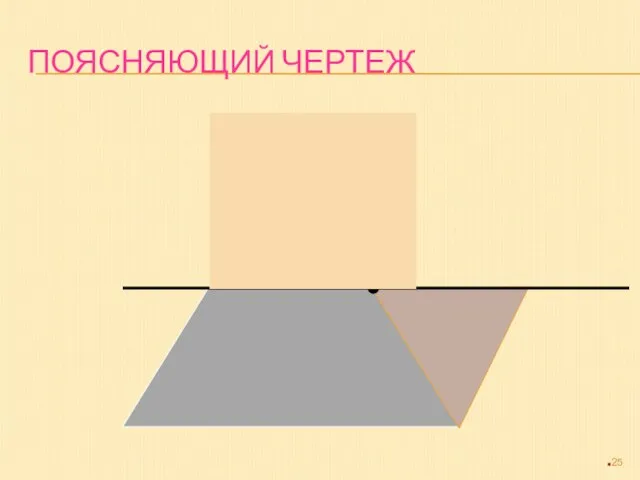
- 24. -Отметим на одной из сторон треугольника точку, которая является серединой этой стороны. -Проведем через эту точку
- 25. ПОЯСНЯЮЩИЙ ЧЕРТЕЖ
- 26. Исходный треугольник и полученный параллелограмм являются равносоставными фигурами, а значит и равновеликими.Мы знаем, что равновеликие фигуры
- 27. Площадь параллелограмма равна произведению его основания на высоту, а высота исходного треугольника по построению в 2
- 29. Скачать презентацию


















 ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии
Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Теорема синусов и косинусов в задачах с практическим содержанием
Теорема синусов и косинусов в задачах с практическим содержанием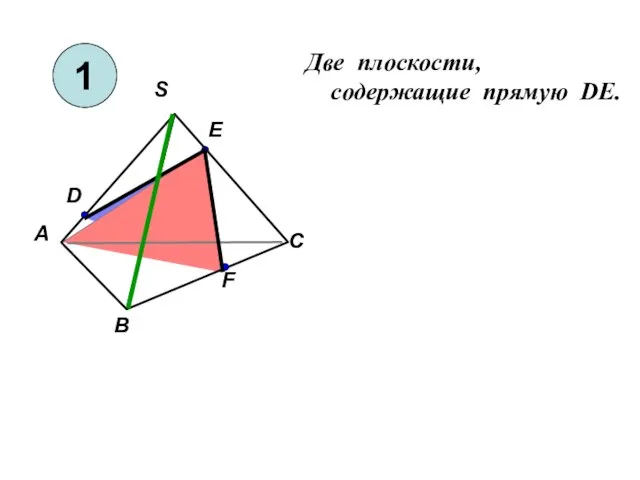 Две плоскости, cодержащие прямую DE
Две плоскости, cодержащие прямую DE Что такое геометрия
Что такое геометрия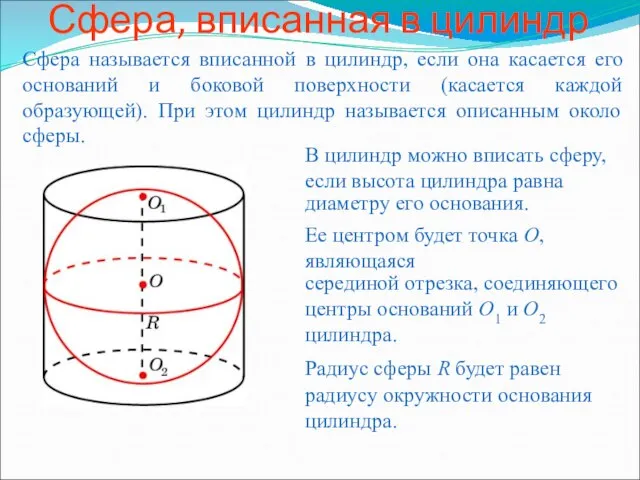 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Многоугольники
Многоугольники Построение графиков гармонических колебаний.
Построение графиков гармонических колебаний. Скалярное произведение в координатах
Скалярное произведение в координатах Теорема о сумме углов треугольника
Теорема о сумме углов треугольника Четырехугольники 9 класс
Четырехугольники 9 класс Признаки равенства треугольников. Устные задачи
Признаки равенства треугольников. Устные задачи Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Орнамент - математическое воплощение красоты
Орнамент - математическое воплощение красоты ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности Признаки паралельности прямых
Признаки паралельности прямых Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Удивительный квадрат (10 класс)
Удивительный квадрат (10 класс) Геометрия в архитектуре
Геометрия в архитектуре Резьба. Крепёжные изделия
Резьба. Крепёжные изделия Свойства производной. Построение графиков функций. (Повторение материала 10 класса).
Свойства производной. Построение графиков функций. (Повторение материала 10 класса). Симметрия
Симметрия Графы
Графы Секреты квадрата и кубика
Секреты квадрата и кубика