Измерение длин отрезков

I. Математический диктант

Вариант 1
1. Из трех точек на прямой только …
2. Отрезком называется …
3. Луч обозначается …
4. Отрезок AB является суммой отрезков AC и CB и обозначается …
5. Если два отрезка равны третьему, то …
6. Умножить отрезок AB на натуральное число n, значит, …
Вариант 2
1. Каждая точка на прямой разбивает эту прямую на …
2. Лучом называется …
3. Отрезок обозначается …
4. Отрезок AC является разностью отрезков AB и CB и обозначается …
5. На любом луче от его начала можно отложить …
6. Разделить отрезок AB на натуральное число n значит, …

Вариант 1
1.лежит между двумя другими
2.часть прямой состоящая из 2 данных точек и всех точек лежащих между ними.
3.AC+CB
4.То они равны
5.Его надо сложить с собой n раз
Вариант 2
1.На две части
2.Часть прямой, сотоящая из точки этой прямой и всех точек, лежащих от нее по одну сторону.
3.AB-CB
4.Один отрезок, равный данному.
5.Деление отрезка на n равных частей

Лабораторная работа.
Возьмем отрезок OE (10 клеток) и назовем его единичным.
2. Теперь возьмем отрезок AB (20 клеток). Сколько раз единичный отрезок OE укладывается в отрезке AB?
Далее возьмем отрезок CD (30 клеток). Сколько раз единичный отрезок OE укладывается в отрезке CD?
Полученные числа 2 и 3 являются соответственно длинами отрезков AB и CD. Можно ввести специальное обозначение для длины отрезка, а именно, |AB|=2, |CD|=3.

3. Возьмем отрезок MN (11 клеток).
Единичный отрезок OE укладывается в данном отрезке один раз и еще остается одна клетка, которая в данном случае равна единичного отрезка. Следовательно, |MN|=1,1.
4. Определим длину отрезка GH (23 клетки) и KL (5 клеток).
|GH|=2,3; |KL|=0,5.
Вывод.
Измерение длины отрезка основано на сравнении его с отрезком, длина которого принимается за единицу (единичный отрезок).

Длина отрезка
– это положительное число, показывающее сколько раз единичный отрезок и его части укладываются в этом отрезке.
Единичный отрезок можно разбивать не только на 10, но и на другое число частей. Так, если единичный отрезок разбит на q равных частей и одна такая часть укладывается в отрезке АВ ровно р раз, то длина отрезка АВ считается равной дроби 8/3 . На рисунке q = 3, р = 8.
Длину отрезка AB называют также расстоянием между точками A и B. Иногда, под расстоянием между точками A и B будем понимать сам отрезок AB.
Длину отрезка АВ будем обозначать так же как и сам отрезок, АВ.

Вопросы
- Возьмем два равных отрезка AB и A1B1. Что можно сказать об их длинах?
- Дан отрезок AC, который является суммой отрезков AB и BC. Что можно сказать о длине суммы этих отрезков?

Свойства длины отрезка :
Свойство 1. Длины равных отрезков равны.
Свойство 2. Длина суммы отрезков равна сумме их длин.

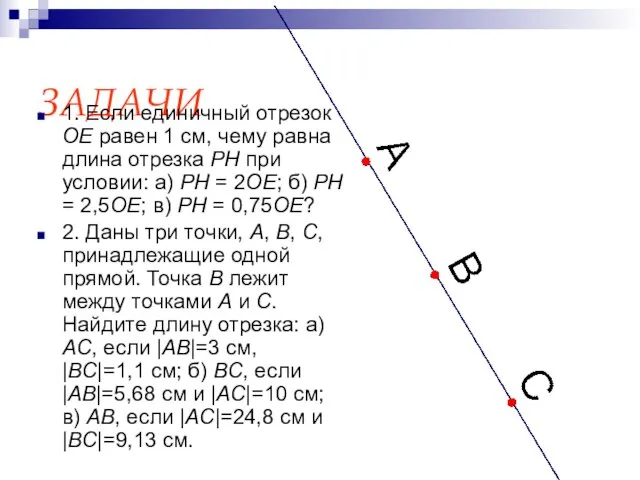
ЗАДАЧИ
1. Если единичный отрезок OE равен 1 см, чему равна длина отрезка PH при условии: а) PH = 2OE; б) PH = 2,5OE; в) PH = 0,75OE?
2. Даны три точки, A, B, C, принадлежащие одной прямой. Точка B лежит между точками A и C. Найдите длину отрезка: а) AC, если |AB|=3 см, |BC|=1,1 см; б) BC, если |AB|=5,68 см и |AC|=10 см; в) AB, если |AC|=24,8 см и |BC|=9,13 см.

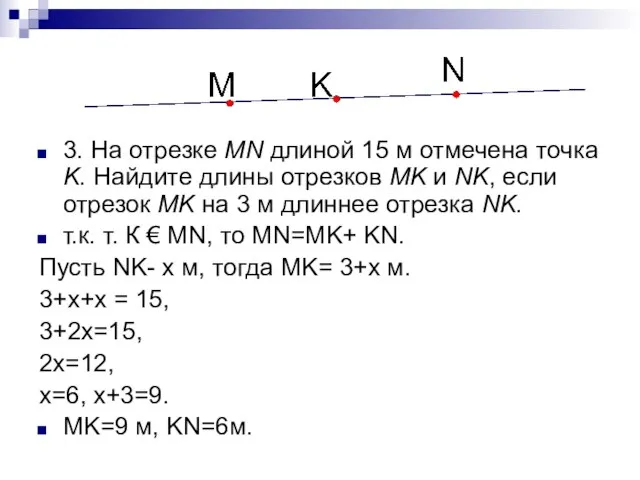
3. На отрезке MN длиной 15 м отмечена точка K. Найдите длины отрезков MK и NK, если отрезок MK на 3 м длиннее отрезка NK.
т.к. т. К € MN, то MN=MK+ KN.
Пусть NK- x м, тогда MK= 3+x м.
3+x+x = 15,
3+2x=15,
2x=12,
x=6, x+3=9.
MK=9 м, KN=6м.

4*. Отрезки AB и AC лежат на одной прямой. Точка O – середина отрезка AB, точка P – середина отрезка AC, лежащая между B и C. Докажите, что BC=2OP.
Решение. BC=BP+PC=
BP+AP=
BP+BP+2OB=
2(BP+OB)=2OP.