Сечения многогранников плоскостью

Работа с текстом задачи
Задача. Построить сечение пятиугольной призмы плоскостью, проходящей через три точки, одна из которых лежит в плоскости верхнего основания, а две другие – на несмежных боковом ребре и ребре нижнего основания.
Определите тип задачи.
Сечение задано тремя точками, не лежащими на одной прямой.
Что дано в задаче?
Дана пятиугольная призма; три точки (в плоскости верхнего основания, на несмежных боковом ребре и ребре нижнего основания).
Что требуется задачей?
Построить сечение данной призмы плоскостью, проходящей через данные точки.
Какие существуют методы построения сечения многогранника плоскостью?
Метод следа; метод внутреннего проектирования.
Нарисуем данные задачи.
Начало

Начало
Иллюстрация условий задачи
Дано: Пятиугольная призма
ABCDEA1B1C1D1E1;
Точки K, M, P.
Построить: Сечение плоскостью, проходящей через
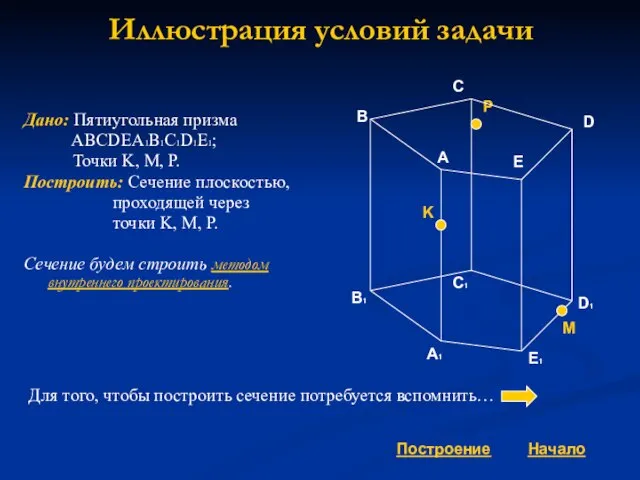
точки K, M, P.
Сечение будем строить методом внутреннего проектирования.
A
B
C
D
E
K
P
Для того, чтобы построить сечение потребуется вспомнить…
A1
E1
D1
B1
C1
M
Построение

Начало
Полезно вспомнить
Аксиомы стереометрии
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Следствия из аксиом
Сл 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Сл 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Свойство параллельных плоскостей
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Стр. 1 1 2

Полезно вспомнить
Призма.
Что называется призмой? Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn, расположенных в параллельных плоскостях, и параллелограммов, называется призмой.
Основные свойства параллельного проектирования
Проекция прямой есть прямая.
Проекция отрезка есть отрезок.
Проекция параллельных отрезков – параллельные отрезки или отрезки, принадлежащие одной прямой.
Проекция параллельных отрезков, а также проекции отрезков, лежащих на одной прямой, пропорциональны самим отрезкам.
Стр. 1 1 2
Начало
Алгоритм построения
a
b
B1
B2
Bn
A1
A2
An
Многоугольники A1A2…An и B1B2…Bn – основания призмы.
Параллелограммы A1A2B2B1, …, AnA1B1Bn – боковые грани.

Алгоритмическое предписание (метод внутреннего проектирования)
да
Сечение задано тремя точками, не лежащими на одной прямой
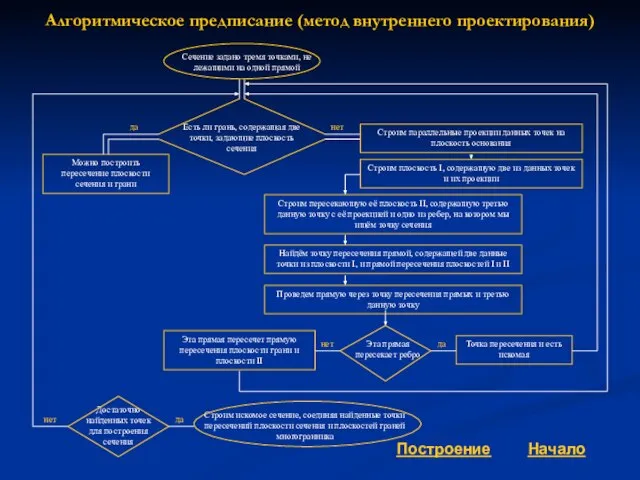
Есть ли грань, содержащая две точки, задающие плоскость сечения
нет
Можно построить пересечение плоскости сечения и грани
Строим параллельные проекции данных точек на плоскость основания
Строим плоскость I, содержащую две из данных точек и их проекции
Строим пересекающую её плоскость II, содержащую третью данную точку с её проекцией и одно из ребер, на котором мы ищём точку сечения
Найдём точку пересечения прямой, содержащей две данные точки из плоскости I, и прямой пересечения плоскостей I и II
Проведем прямую через точку пересечения прямых и третью данную точку
Эта прямая пересекает ребро
Точка пересечения и есть искомая
Эта прямая пересечет прямую пересечения плоскости грани и плоскости II
Достаточно найденных точек для построения сечения
нет
Строим искомое сечение, соединяя найденные точки пересечений плоскости сечения и плоскостей граней многогранника
нет
да
да
Начало
Построение