Координаты вектора

КООРДИНАТЫ ВЕКТОРА
Теорема. Вектор имеет координаты (x, y, z) тогда и только тогда, когда он представим в виде
Доказательство. Отложим вектор от начала координат и его конец обозначим через А. Имеет место равенство
Точка А имеет координаты (x, y, z) тогда и только тогда, когда выполняются равенства
и, значит,

ДЛИНА ВЕКТОРА
Если вектор задан координатами начальной и конечной точек, A1(x1, y1, z1), A2(x2, y2, z2), то его длина выражается формулой

Упражнение 1
Найдите координаты векторов:
а)
б)
в)
г)
Ответ: а) (-2, 6, 1);
б) (1, 3, 0);
в) (0, -3, 2);
г) (-5, 0, 5).

Упражнение 2
Найдите координаты вектора , если: a) A(2, -6, 9), B(-5, 3, -7); б) A(1, 3, -8), B(6, -5, -10); в) A(-3, 1, -20), B(5, 1, -1).
Ответ: а) (-7, 9, -16);
б) (5, -8, -2);
в) (8, 0, 19).

Упражнение 3
Вектор имеет координаты (a,b,c). Найдите координаты вектора .
Ответ: (-a, -b, -c).

Упражнение 4
В прямоугольном параллелепипеде OABCO1A1B1C1 вершина O – начало координат, ребра OA, OC, OO1 лежат на осях координат Ox, Oy и Oz соответственно и OA=2, OC=3, OO1=4. Найдите координаты векторов , , , .
Ответ: (2, 0, 4); (2, 3, 4); (0, 0, 4); (0, 3, 0).

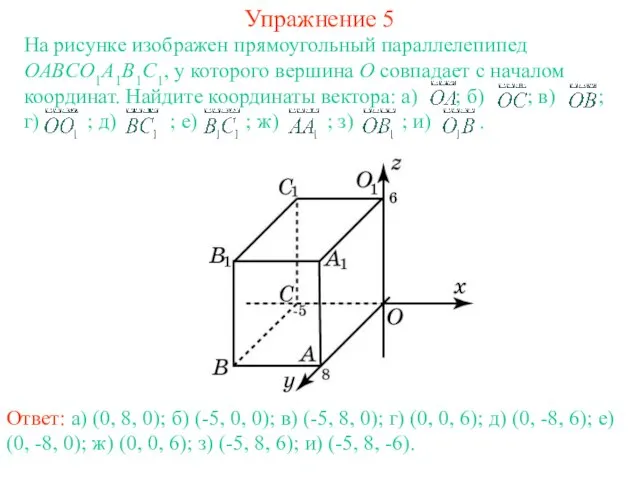
Упражнение 5
На рисунке изображен прямоугольный параллелепипед OABCO1A1B1C1, у которого вершина O совпадает с началом координат. Найдите координаты вектора: а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з) ; и) .
Ответ: а) (0, 8, 0); б) (-5, 0, 0); в) (-5, 8, 0); г) (0, 0, 6); д) (0, -8, 6); е) (0, -8, 0); ж) (0, 0, 6); з) (-5, 8, 6); и) (-5, 8, -6).

Упражнение 6
Найдите координаты векторов и , если (1, 0, 2), (0,3,-4).
Ответ: (1, 3, -2); (1, -3, 6).

Упражнение 7
Даны векторы (-1,2,8) и (2,-4,3). Найдите координаты векторов:
а) ;
б) ;
в) .

Упражнение 8
Найдите координаты точки N, если вектор имеет координаты (4, -3, 0) и точка M - (1, -3, -7).
Ответ: (5, -6, -7).

Упражнение 9
Какому условию должны удовлетворять координаты вектора, чтобы он был: а) перпендикулярен координатной плоскости Oxy; б) параллелен координатной прямой Ox?
Ответ: а) Первая и вторая координаты равны нулю;
б) вторая и третья координаты равны нулю.

Упражнение 10
Найдите координаты конца единичного вектора с началом в точке A(1, 2, 3) и: а) перпендикулярного плоскости Oxy; б) параллельного прямой Ox.
Ответ: а) (1,2,4), (1,2,2);
б) (2,2,3), (0,2,3).