Содержание
- 2. Цели урока: Ввести определение скрещивающихся прямых. Ввести формулировки и доказать признак и свойство скрещивающихся прямых.
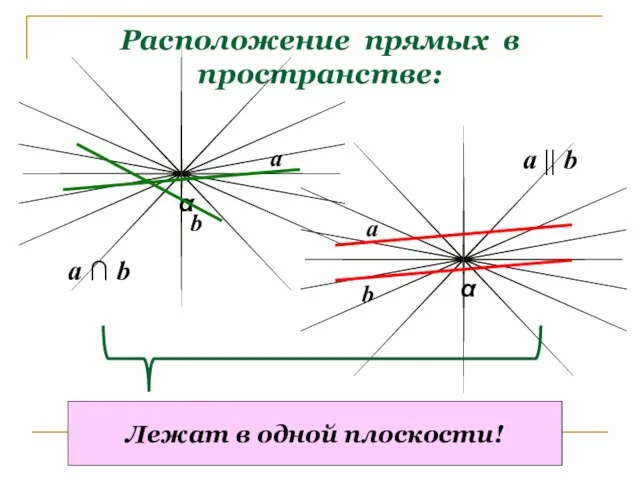
- 3. Расположение прямых в пространстве: α α a b a b a ∩ b a || b
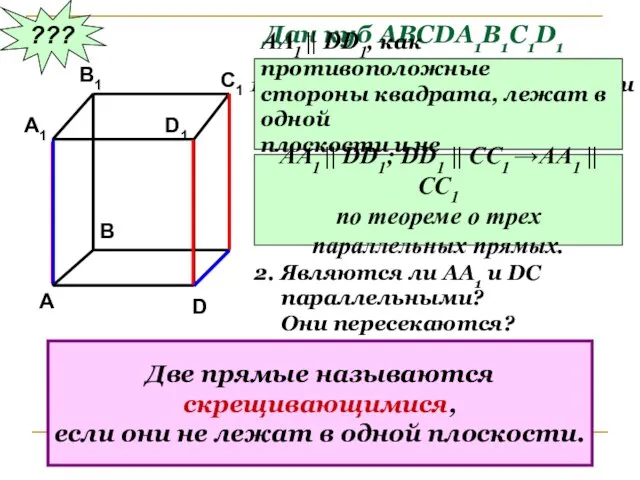
- 4. ??? Дан куб АВСDA1B1C1D1 Являются ли параллельными прямые АА1 и DD1; АА1 и СС1 ? Почему?
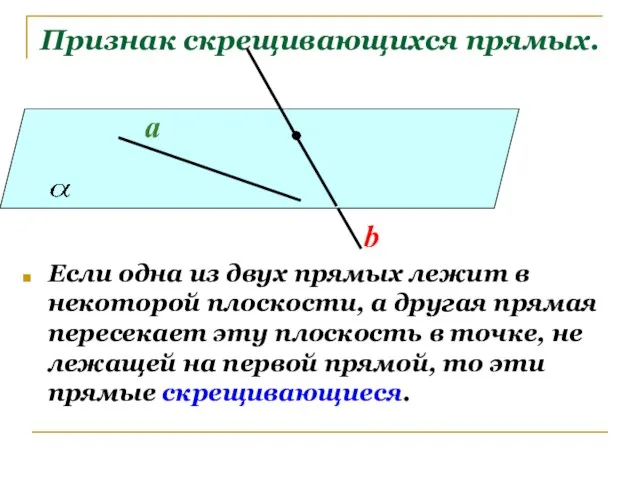
- 5. Признак скрещивающихся прямых. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает
- 6. Признак скрещивающихся прямых. Дано: АВ α, СD ∩ α = С, С АВ. a b Доказательство:
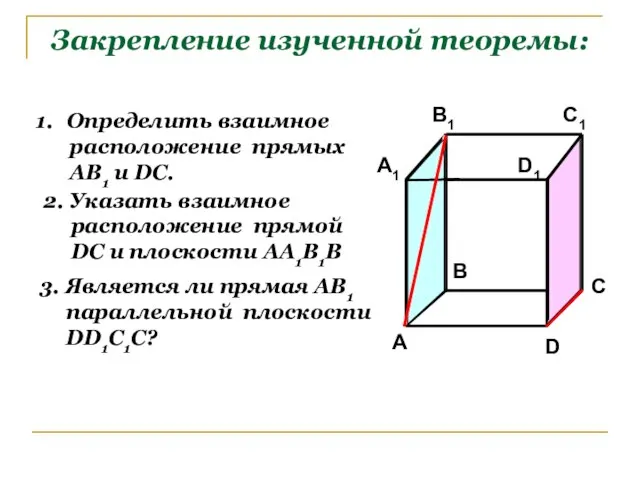
- 7. Закрепление изученной теоремы: Определить взаимное расположение прямых АВ1 и DC. 2. Указать взаимное расположение прямой DC
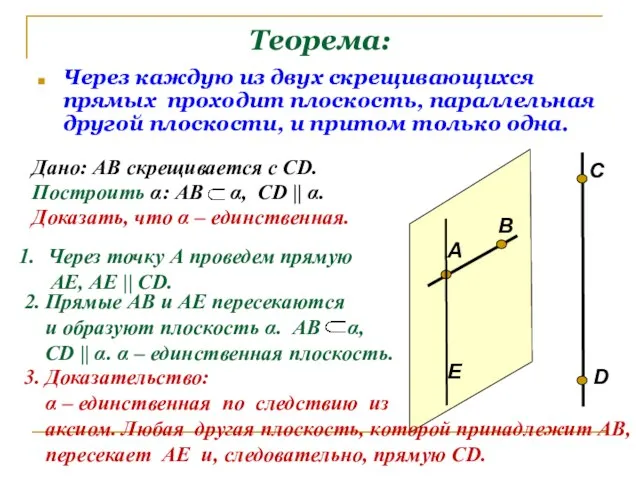
- 8. Теорема: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой плоскости, и притом только одна.
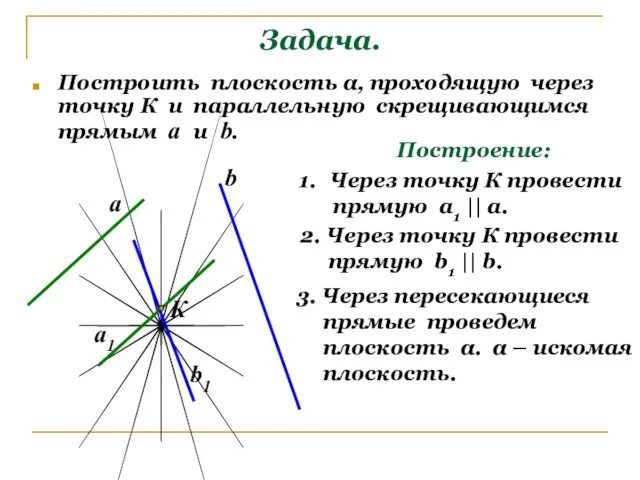
- 9. Задача. Построить плоскость α, проходящую через точку К и параллельную скрещивающимся прямым а и b. Построение:
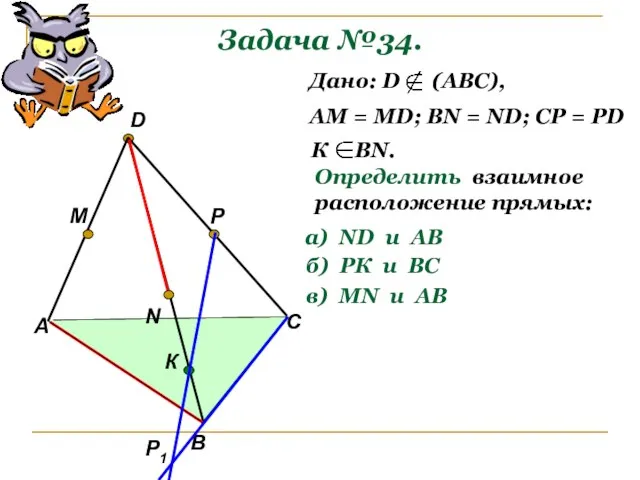
- 10. Задача №34. А В С D M N P Р1 К Дано: D (АВС), АМ =
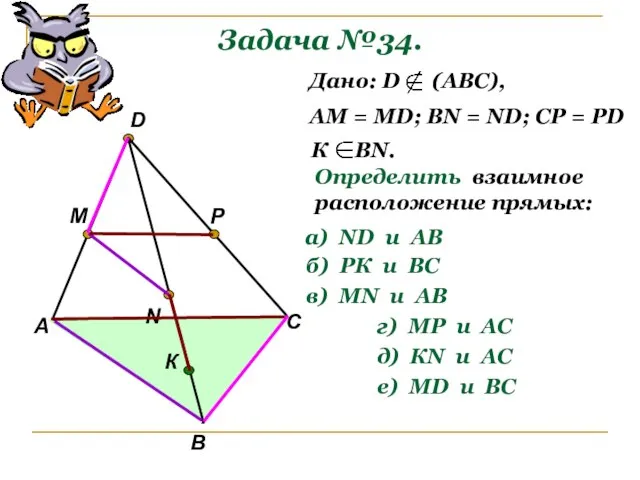
- 11. Задача №34. А В С D M N P К Дано: D (АВС), АМ = МD;
- 13. Скачать презентацию


 Построение четвёртого пропорционального отрезка
Построение четвёртого пропорционального отрезка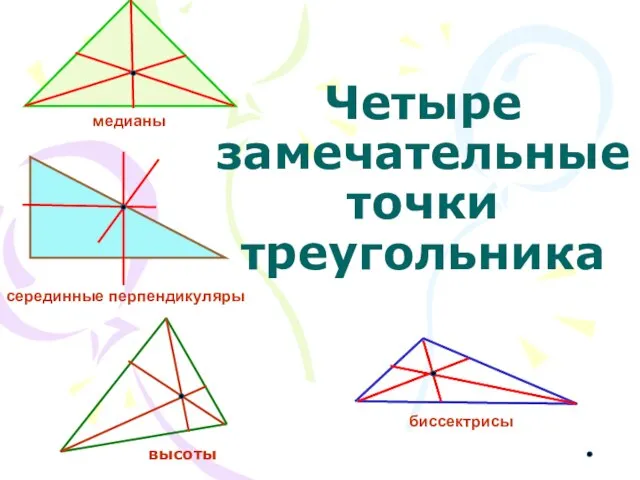 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника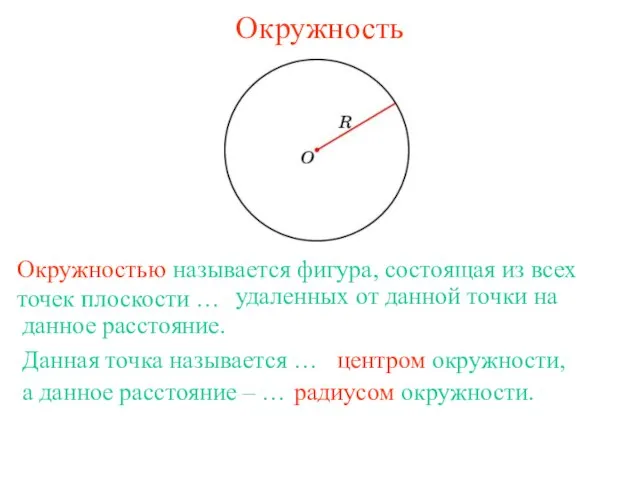 Окружность
Окружность Первый признак равенства треугольников
Первый признак равенства треугольников Геометрия
Геометрия Подготовлю справочник по геометрии (или как повторить геометрию к экзамену)
Подготовлю справочник по геометрии (или как повторить геометрию к экзамену) Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Площади
Площади Циклоида
Циклоида Планиметрия - презентация по Геометрии_
Планиметрия - презентация по Геометрии_ Площадь параллелограмма 9 класс
Площадь параллелограмма 9 класс Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Геометрия. Как она возникла?
Геометрия. Как она возникла? Основные труды и биография Декарта
Основные труды и биография Декарта Признаки равенства треугольников
Признаки равенства треугольников Двумерный симплекс история его изучения
Двумерный симплекс история его изучения Применение подобия к доказательству теорем и решению задач
Применение подобия к доказательству теорем и решению задач Правильные многогранники
Правильные многогранники Презентация на тему: Сечение
Презентация на тему: Сечение Параллелограмм
Параллелограмм Площади многоугольников
Площади многоугольников Разрезание и складывание плоских фигур
Разрезание и складывание плоских фигур В гостях у Геометрии - презентация по Геометрии_
В гостях у Геометрии - презентация по Геометрии_ Многогранники вокруг нас
Многогранники вокруг нас Площади (8 класс)
Площади (8 класс) Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми
Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми Классическое определение вероятности. Комбинаторные методы решения задач
Классическое определение вероятности. Комбинаторные методы решения задач Медиана, биссектриса и высота треугольника
Медиана, биссектриса и высота треугольника