Четыре замечательные точки треугольника

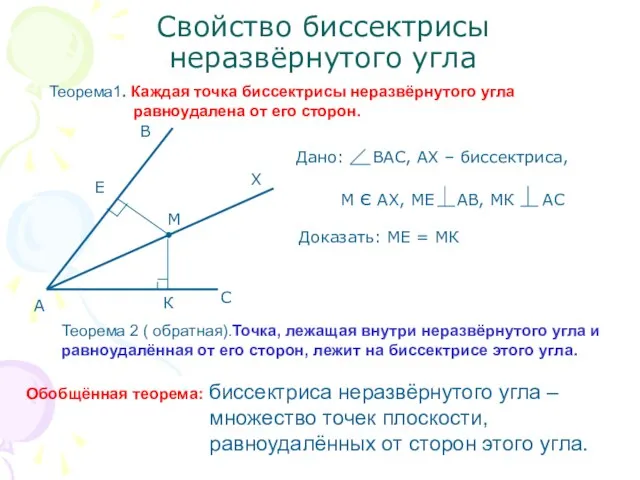
Свойство биссектрисы неразвёрнутого угла
Теорема1. Каждая точка биссектрисы неразвёрнутого угла
равноудалена от его сторон.
Доказать: МЕ = МК
Теорема 2 ( обратная).Точка, лежащая внутри неразвёрнутого угла и равноудалённая от его сторон, лежит на биссектрисе этого угла.
Обобщённая теорема: биссектриса неразвёрнутого угла –
множество точек плоскости,
равноудалённых от сторон этого угла.

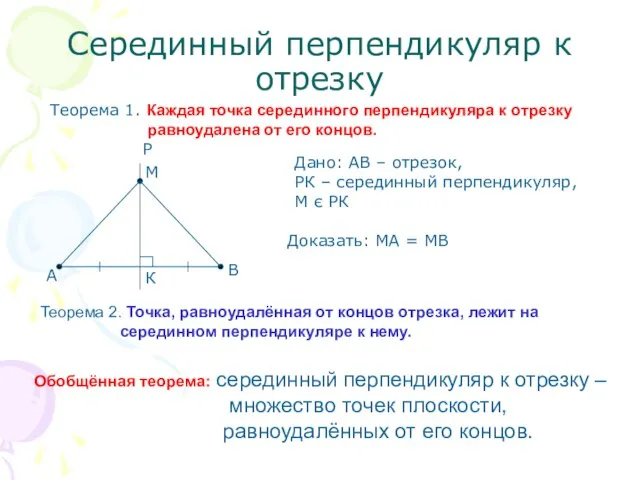
Серединный перпендикуляр к отрезку
Теорема 1. Каждая точка серединного перпендикуляра к отрезку
равноудалена от его концов.
Дано: АВ – отрезок,
РК – серединный перпендикуляр,
М є РК
Доказать: МА = МВ
Теорема 2. Точка, равноудалённая от концов отрезка, лежит на
серединном перпендикуляре к нему.
Обобщённая теорема: серединный перпендикуляр к отрезку –
множество точек плоскости,
равноудалённых от его концов.

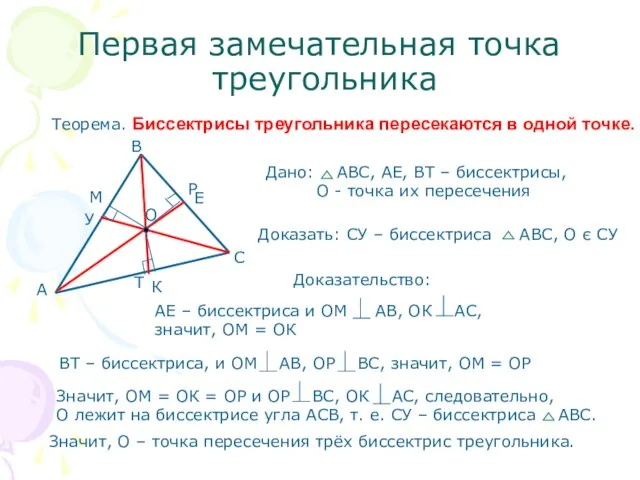
Первая замечательная точка
треугольника
Теорема. Биссектрисы треугольника пересекаются в одной точке.
Доказательство:
Значит, О – точка пересечения трёх биссектрис треугольника.

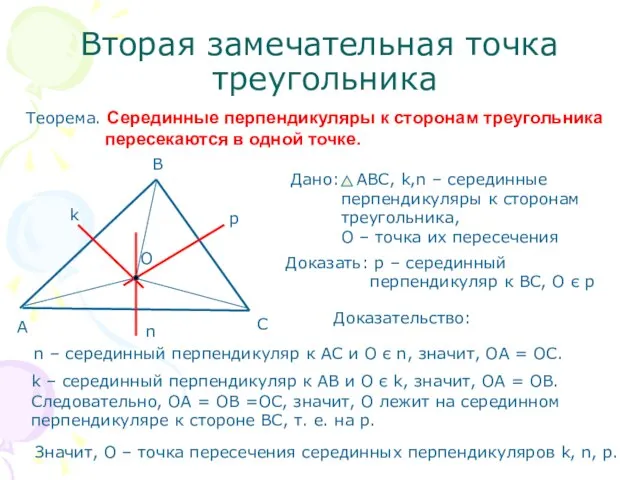
Вторая замечательная точка
треугольника
Теорема. Серединные перпендикуляры к сторонам треугольника
пересекаются в одной точке.
Доказать: р – серединный
перпендикуляр к ВС, О є р
Доказательство:
n – серединный перпендикуляр к АС и О є n, значит, ОА = ОС.
k – серединный перпендикуляр к АВ и О є k, значит, ОА = ОВ.
Следовательно, ОА = ОВ =ОС, значит, О лежит на серединном
перпендикуляре к стороне ВС, т. е. на р.
Значит, О – точка пересечения серединных перпендикуляров k, n, p.

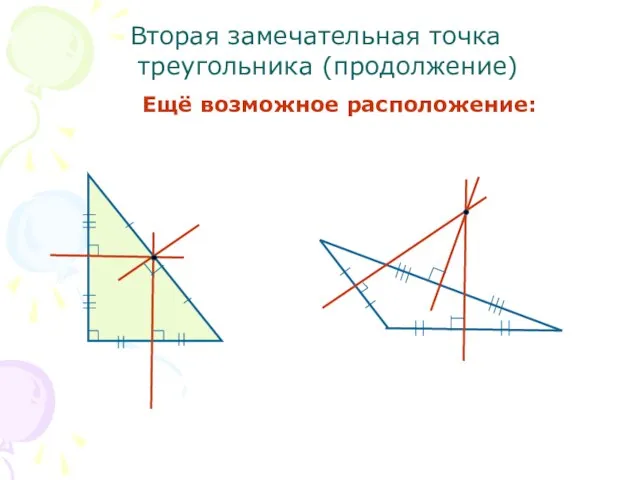
Вторая замечательная точка
треугольника (продолжение)
Ещё возможное расположение:

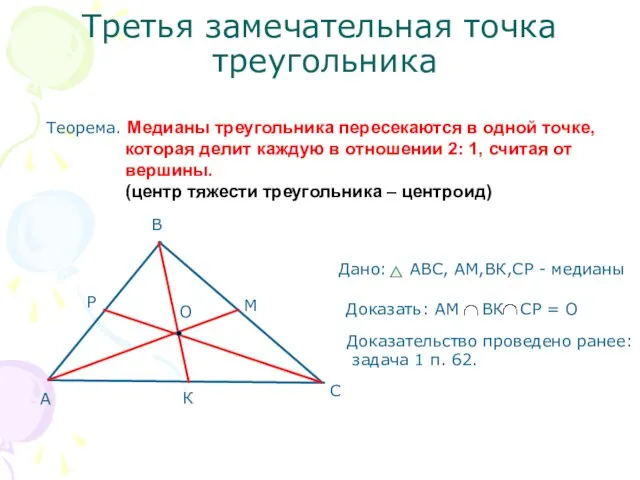
Третья замечательная точка
треугольника
Теорема. Медианы треугольника пересекаются в одной точке,
которая делит каждую в отношении 2: 1, считая от
вершины.
(центр тяжести треугольника – центроид)
А
В
С
М
К
Р
О
Доказать: АМ ВК СР = О
Доказательство проведено ранее:
задача 1 п. 62.

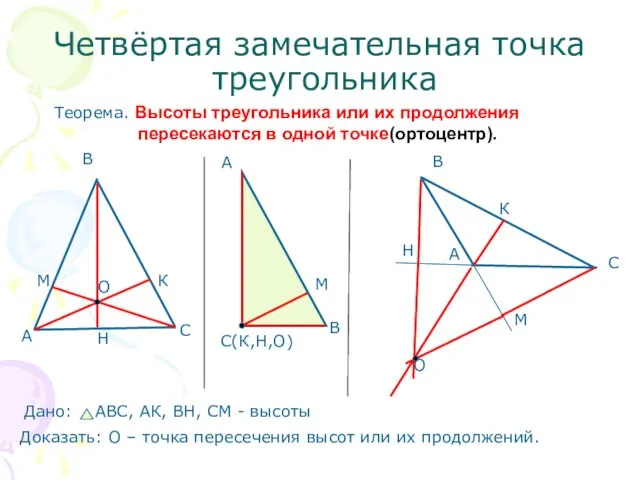
Четвёртая замечательная точка
треугольника
Теорема. Высоты треугольника или их продолжения
пересекаются в одной точке(ортоцентр).

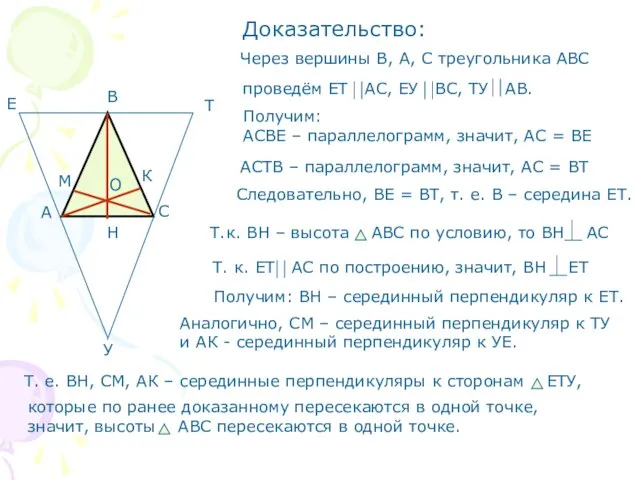
Доказательство:
Получим:
АСВЕ – параллелограмм, значит, АС = ВЕ
АСТВ – параллелограмм, значит, АС = ВТ
Следовательно, ВЕ = ВТ, т. е. В – середина ЕТ.
Получим: ВН – серединный перпендикуляр к ЕТ.
Аналогично, СМ – серединный перпендикуляр к ТУ
и АК - серединный перпендикуляр к УЕ.