Содержание
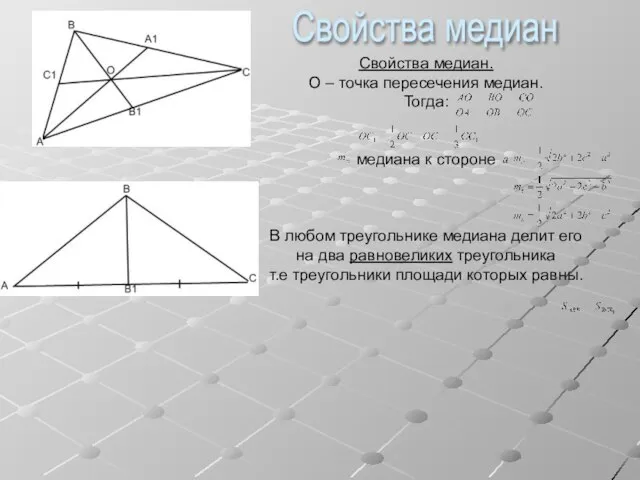
- 2. Свойства медиан. О – точка пересечения медиан. Тогда: медиана к стороне В любом треугольнике медиана делит
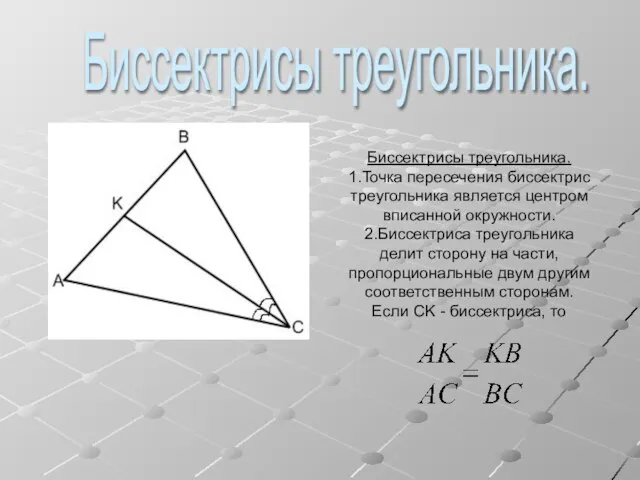
- 3. Биссектрисы треугольника. 1.Точка пересечения биссектрис треугольника является центром вписанной окружности. 2.Биссектриса треугольника делит сторону на части,
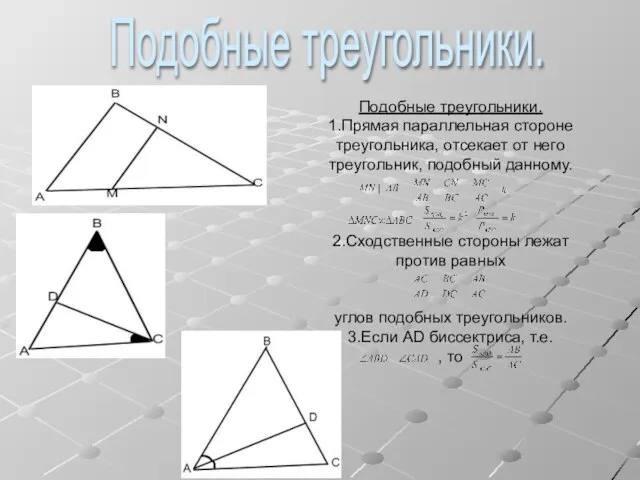
- 4. Подобные треугольники. 1.Прямая параллельная стороне треугольника, отсекает от него треугольник, подобный данному. 2.Сходственные стороны лежат против
- 5. Задача 1. Основание равнобедренного треугольникаравно30 см, а высота, проведённая из вершины основания 24 см. Найти S
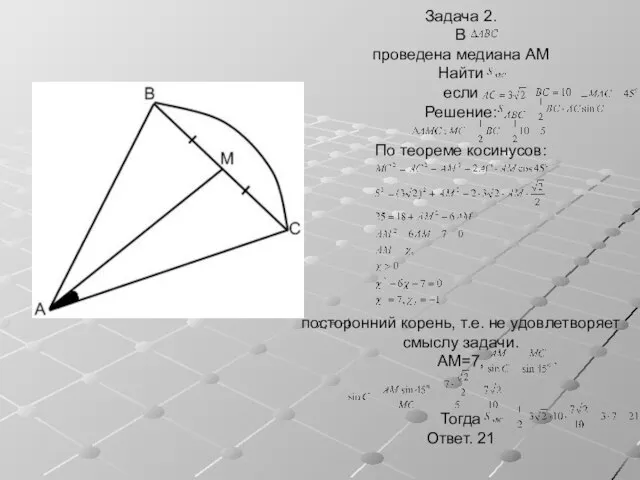
- 6. Задача 2. В проведена медиана AM Найти если Решение: По теореме косинусов: посторонний корень, т.е. не
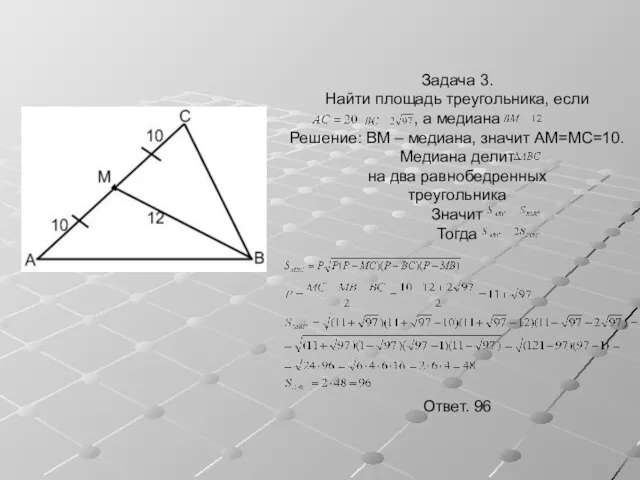
- 7. Задача 3. Найти площадь треугольника, если , а медиана Решение: BM – медиана, значит AM=MC=10. Медиана
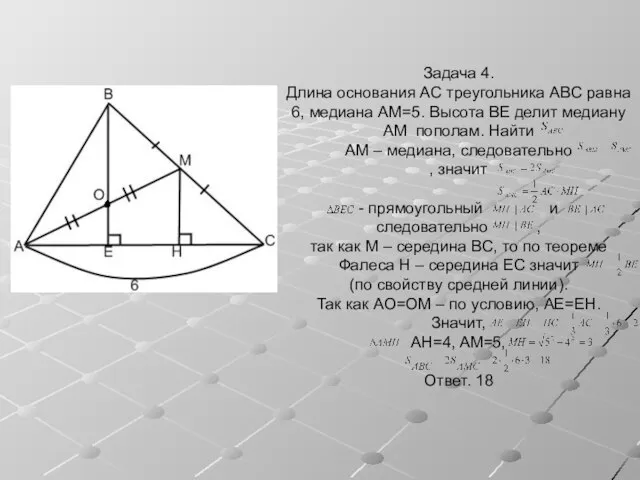
- 8. Задача 4. Длина основания AC треугольника ABC равна 6, медиана AM=5. Высота BE делит медиану AM
- 10. Скачать презентацию

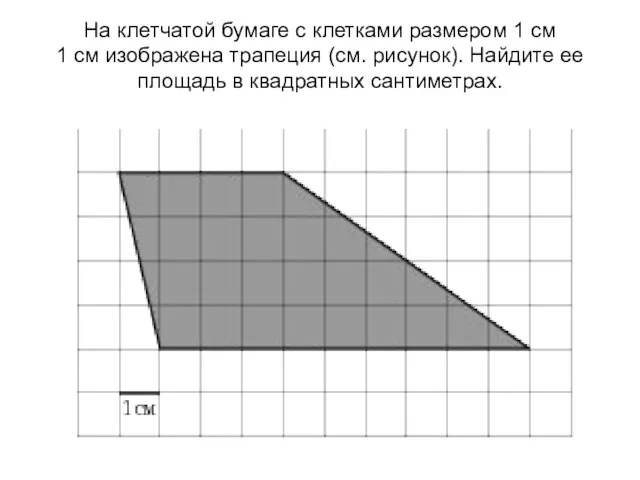 Площади фигур на клетке
Площади фигур на клетке Тетраэдр
Тетраэдр Формула Гириха
Формула Гириха Преобразование графиков функций - презентация по Геометрии__________________________________________________________________________________________________________________
Преобразование графиков функций - презентация по Геометрии__________________________________________________________________________________________________________________ Многоугольники
Многоугольники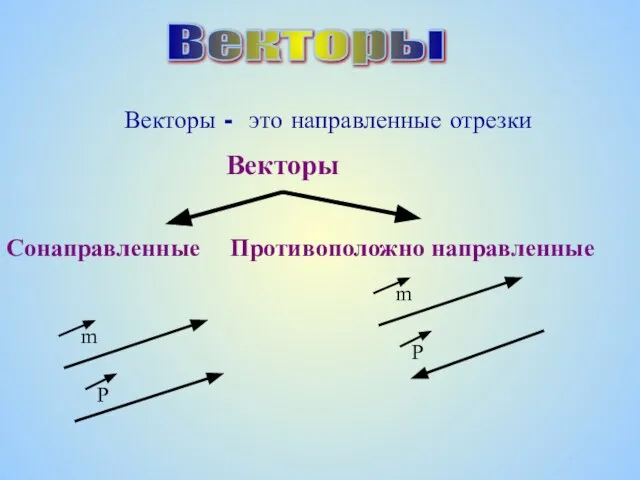 Векторы: Знакомство
Векторы: Знакомство Площади многоугольников
Площади многоугольников Измерение углов
Измерение углов Начертательная геометрия
Начертательная геометрия Что изучает геометрия 7 класс
Что изучает геометрия 7 класс Симметрия
Симметрия УСТНЫЕ ЗАДАЧИ ПО ТЕМЕ "ПРИЗМА"
УСТНЫЕ ЗАДАЧИ ПО ТЕМЕ "ПРИЗМА" Окружность и круг
Окружность и круг Решение задач на нахождение периметра и площади
Решение задач на нахождение периметра и площади Геометрические задачи на экстремум
Геометрические задачи на экстремум Подготовлю справочник по геометрии (или как повторить геометрию к экзамену)
Подготовлю справочник по геометрии (или как повторить геометрию к экзамену) Площадь многоугольника 8 класс
Площадь многоугольника 8 класс В мире треугольников
В мире треугольников Планиметрия
Планиметрия Измерение длин отрезков
Измерение длин отрезков Вводное повторение курса геометрии
Вводное повторение курса геометрии Правильная пирамида
Правильная пирамида Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Площади плоских геометрических фигур
Площади плоских геометрических фигур Доклад о «Сфере и шаре»
Доклад о «Сфере и шаре» Сечения многогранников плоскостью
Сечения многогранников плоскостью Теорема синусов и косинусов в задачах с практическим содержанием
Теорема синусов и косинусов в задачах с практическим содержанием Симметрия правит миром
Симметрия правит миром