Содержание
- 2. Определения Сфера-это фигура, состоящая из всех точек пространства, удалённых от данной точки на данном расстоянии. Шар-это
- 3. Площадь сферы Для определения площади сферы воспользуемся понятием описанного многогранника. Многогранник называется описанным около сферы (шара)
- 4. .. Точка О называется центром сферы, R-радиус сферы. Любой отрезок, соединяющий центр и какую-нибудь точку сферы,
- 5. шар Граница шара называется шаровой поверхностью или сферой. Отрезок, соединяющий две точки шаровой поверхности и проходящий
- 6. Уравнение сферы В прямоугольной системе координат уравнение сферы радиуса R с центром С (х0;у0;z0) имеет вид
- 7. Шаровой сегмент Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью. Круг, получившийся в сечении,
- 9. Скачать презентацию






 Что такое геометрия
Что такое геометрия ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ
ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ Лабораторный практикум по геометрии 7 класс
Лабораторный практикум по геометрии 7 класс Геометрия. Как она возникла?
Геометрия. Как она возникла?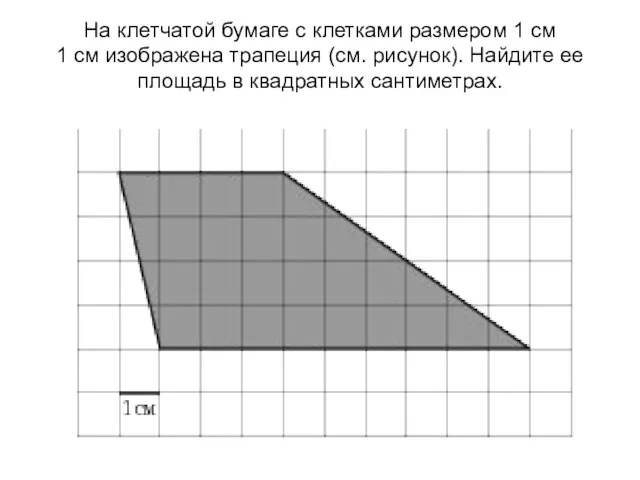 Площади фигур на клетке
Площади фигур на клетке Свойство скрещивающихся рёбер правильной треугольной пирамиды
Свойство скрещивающихся рёбер правильной треугольной пирамиды Стереометрия в образах
Стереометрия в образах Многообразие многоугольников
Многообразие многоугольников Геометрические задачи «С2» - презентация по Геометрии_
Геометрические задачи «С2» - презентация по Геометрии_ Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска
Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник
Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ
ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ Площадь квадрата, прямоугольника, параллелограмма - презентация по Геометрии_
Площадь квадрата, прямоугольника, параллелограмма - презентация по Геометрии_ Бозон Хиддинса
Бозон Хиддинса Цилиндр. Конус. Шар
Цилиндр. Конус. Шар Площадь многоугольника 8 класс
Площадь многоугольника 8 класс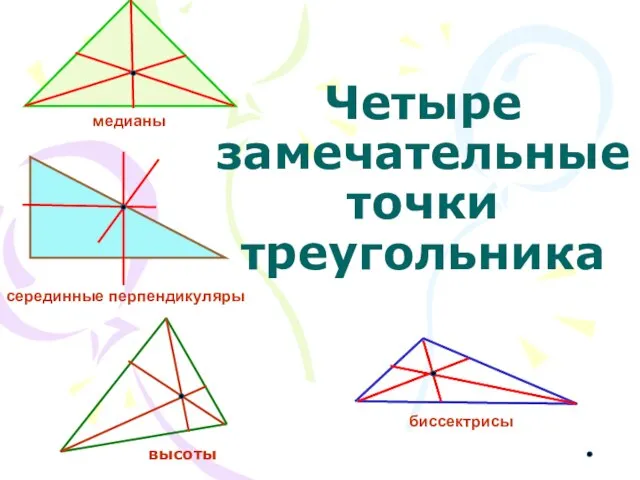 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника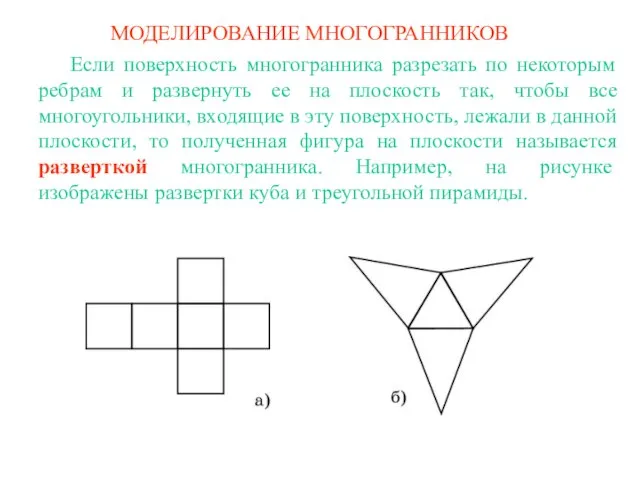 Моделирование многогранников
Моделирование многогранников Площадь прямоугольного треугольника
Площадь прямоугольного треугольника Логарифм. Основные понятия
Логарифм. Основные понятия Расстояние от точки до прямой
Расстояние от точки до прямой Объём пирамиды
Объём пирамиды тренажёр по теме смежные и вертикальные углы
тренажёр по теме смежные и вертикальные углы Вычисление угла между прямыми и плоскостями
Вычисление угла между прямыми и плоскостями Тригонометрические неравенства
Тригонометрические неравенства Бумажные складные модели и их использование на уроках геометрии в 10 классе
Бумажные складные модели и их использование на уроках геометрии в 10 классе Удивительный квадрат (10 класс)
Удивительный квадрат (10 класс) Параллелепипед
Параллелепипед