соответственно, к уменьшению энергии связи
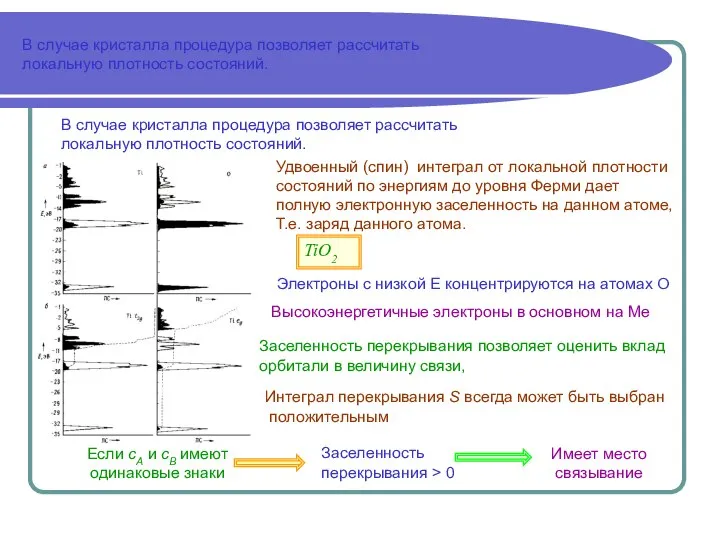
Уменьшение или увеличение числа электронов приведет к понижению полной
заселенности перекрывания и, соответственно, к уменьшению энергии связи
Полная заселенность перекрывания.
По смыслу близка к порядку связи
Твердое тело
Большая молекула, имеющая
большое число электронных состояний.
.
Соседние уровни располагаются
на одинаковом расстоянии по оси k
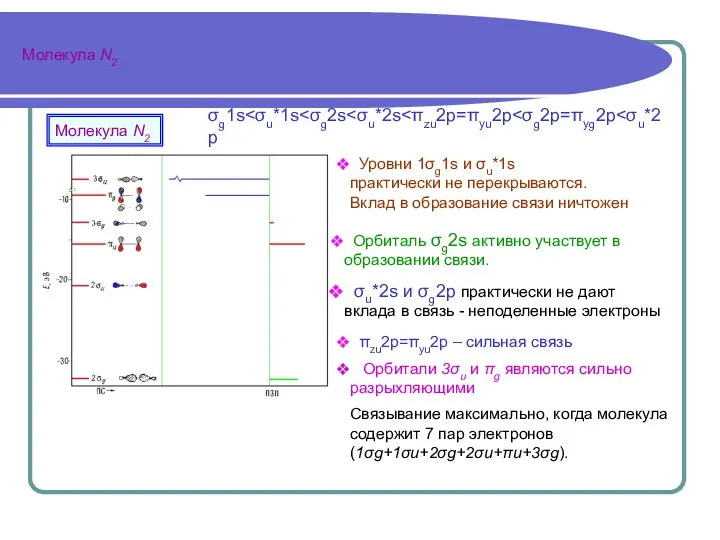
Если просуммировать заселенность перекрывания по всем имеющимся
у системы орбиталям с учетом их
заполнения электронами
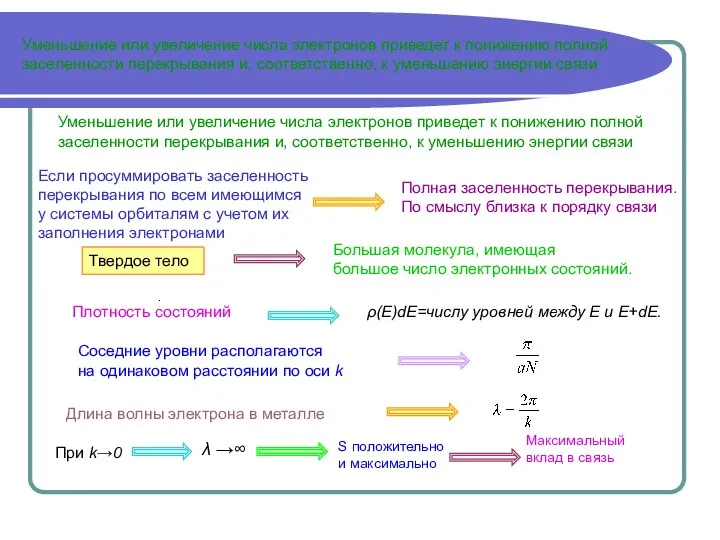
ρ(Е)dE=числу уровней между E и E+dE.
Плотность состояний
Длина волны электрона в металле
При k→0
λ →∞
S положительно и максимально
Максимальный вклад в связь

 Коррозия металлов
Коррозия металлов Органическая химия: пищевые добавки
Органическая химия: пищевые добавки Ионная связь
Ионная связь Презентация на тему Углекислый газ
Презентация на тему Углекислый газ  Химическая связь
Химическая связь 10_kl_klas-ya
10_kl_klas-ya Срспальфа-олефинсульфанаттар
Срспальфа-олефинсульфанаттар Презентация на тему Химическая связь
Презентация на тему Химическая связь  Презентация на тему Мыло. Синтетические моющие средства
Презентация на тему Мыло. Синтетические моющие средства  Электролиз. Применение электролиза
Электролиз. Применение электролиза Растительные источники жиров и жирных масел
Растительные источники жиров и жирных масел Periodická soustava prvků
Periodická soustava prvků Презентация на тему Кристаллические решетки 9 класс
Презентация на тему Кристаллические решетки 9 класс  Ароматические углеводороды. Галогенопроизводные
Ароматические углеводороды. Галогенопроизводные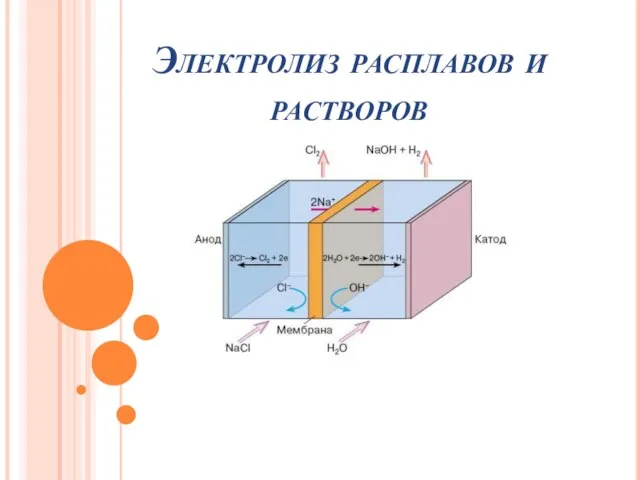 Электролиз расплавов растворов
Электролиз расплавов растворов Углеводы (сахара). Строение, свойства, участие в функционировании живых систем
Углеводы (сахара). Строение, свойства, участие в функционировании живых систем Реакция полимеризации
Реакция полимеризации Роль элементов 5 группы
Роль элементов 5 группы Вермикулитовый концентрат
Вермикулитовый концентрат Метод проектов: организация деятельности по химии
Метод проектов: организация деятельности по химии Творческий отчет кружка Юные химики
Творческий отчет кружка Юные химики Системно-деятельностный подход в обучении химии
Системно-деятельностный подход в обучении химии Aurul, caracteristici, stare
Aurul, caracteristici, stare Опасные химические вещества и их поражающее действие на организм человека
Опасные химические вещества и их поражающее действие на организм человека Современные способы защиты ОТТ
Современные способы защиты ОТТ Катализ в нефтепереработке
Катализ в нефтепереработке Материаловедение. Технология конструкционных материалов. Диаграмма состояния Fe-Fe3C
Материаловедение. Технология конструкционных материалов. Диаграмма состояния Fe-Fe3C Чистые вещества и смеси
Чистые вещества и смеси