Содержание
- 2. Оглавление: Вектор Матрица Многогранник Многоугольник Определитель Система Система координат Стереометрия Уравнение плоскости
- 3. Вектор направленный отрезок, для которого указаны начало и конец. Основные понятия Виды векторов Равенство векторов Сложение
- 4. Основные понятия Векторы можно записать двумя большими латинскими буквами: Векторы также записывают маленькими латинскими буквами: Длиной
- 5. Виды векторов Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных
- 6. Равенство векторов Векторы называются равными, если они сонаправлены и их длины равны. Теорема: от любой точки
- 7. Сложение векторов Правило треугольника Переместительный закон Сочетательный закон Разность векторов Правило многоугольника Правило параллелограмма
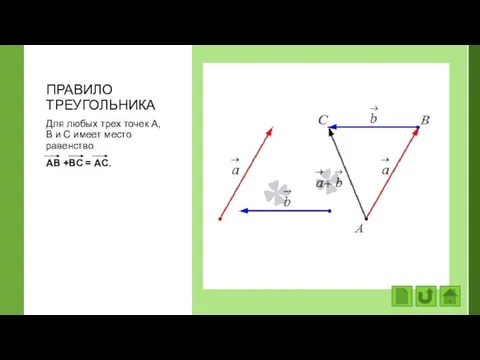
- 8. ПРАВИЛО ТРЕУГОЛЬНИКА Для любых трех точек А, В и С имеет место равенство АВ +ВС =
- 9. Переместительный закон
- 10. Сочетательный закон
- 11. Разность векторов
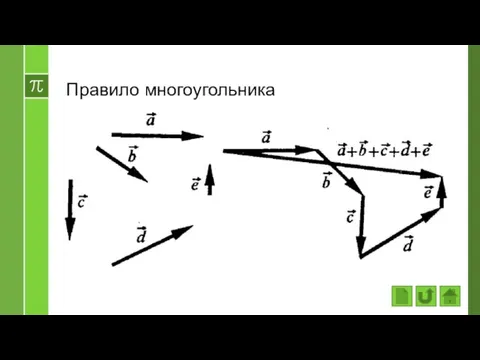
- 12. Правило многоугольника
- 13. Правило параллелограмма
- 14. Умножение вектора на число
- 15. Компланарные векторы
- 16. Координаты вектора
- 17. Сумма и разность векторов, умножение вектора на число. имеет координаты
- 18. Длина вектора Расстояние между двумя точками
- 19. Скалярное произведение векторов
- 20. Матрица математический объект, записываемый в виде прямоугольной таблицы, которая представляет собой совокупность строк и столбцов, на
- 21. Многогранник геометрическое тело, поверхность которого состоит из конечного числа плоских многоугольников. Выпуклый многогранник Правильный многогранник Теорема
- 22. Выпуклый многогранник многогранник, который расположен по одну сторону плоскости, проведённой через любой многоугольник, образующий поверхность данного
- 23. Правильный многогранник многогранник, у которого грани являются правильными многоугольниками с одним и тем же числом сторон
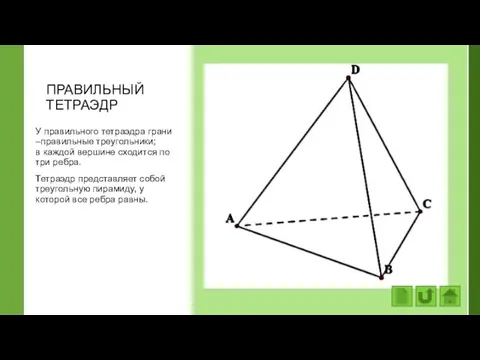
- 24. ПРАВИЛЬНЫЙ ТЕТРАЭДР У правильного тетраэдра грани –правильные треугольники; в каждой вершине сходится по три ребра. Тетраэдр
- 25. КУБ У куба (правильный гексаэдр) все грани – квадраты; в каждой вершине сходится по три ребра.
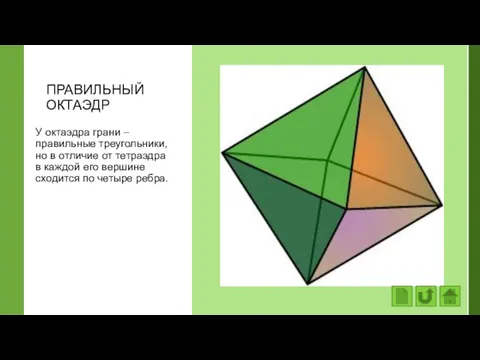
- 26. ПРАВИЛЬНЫЙ ОКТАЭДР У октаэдра грани – правильные треугольники, но в отличие от тетраэдра в каждой его
- 27. ПРАВИЛЬНЫЙ ДОДЕКАЭДР У додекаэдра грани – правильные пятиугольники. В каждой вершине сходится по три ребра.
- 28. ПРАВИЛЬНЫЙ ИКОСАЭДР У икосаэдра грани – правильные треугольники, но в отличие от тетраэдра и октаэдра в
- 29. Теорема Эйлера Если V — число вершин выпуклого многогранника, R — число его ребер и G
- 30. Призма многогранник, состоящий из двух плоских многоугольников, которые лежат в разных плоскостях и совмещаются параллельным переносом,
- 31. Свойства призмы Основания призмы равны и лежат в параллельных плоскостях. Боковые рёбра призмы равны и параллельны.
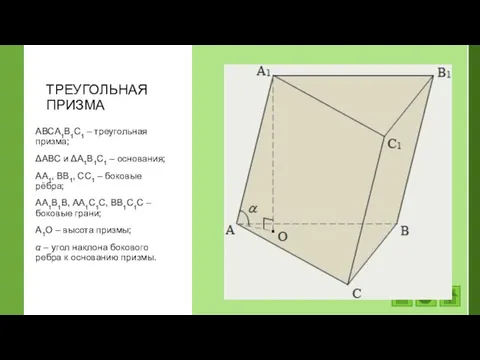
- 32. ТРЕУГОЛЬНАЯ ПРИЗМА АВСA1В1С1 – треугольная призма; ΔАВС и ΔA1В1С1 – основания; АA1, ВВ1, СС1 – боковые
- 33. ПРЯМАЯ ПРИЗМА Призма называется прямой, если её рёбра перпендикулярны плоскостям оснований. В противном случае призма называется
- 34. Параллелепипед призма, в основании которой лежит параллелограмм. Свойства параллелепипеда Прямоугольный параллелепипед Куб Плоскости симметрии
- 35. Свойства параллелепипеда У параллелепипеда все грани – параллелограммы. Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.
- 36. ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД Прямоугольным параллелепипедом называется такой прямой параллелепипед, в основании которого лежит прямоугольник. Свойства: Все грани
- 37. КУБ Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом. Диагональ куба в квадратный корень
- 38. Плоскости симметрии В прямоугольном параллелепипеде, как и во всяком параллелепипеде, есть центр симметрии – точка пересечения
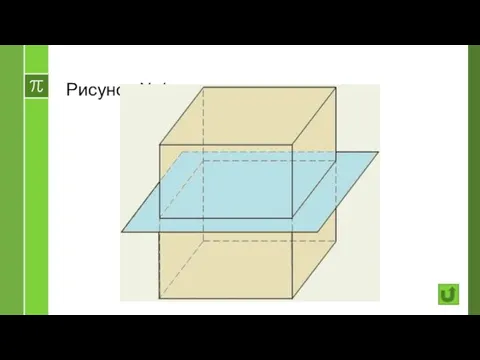
- 39. Рисунок №1
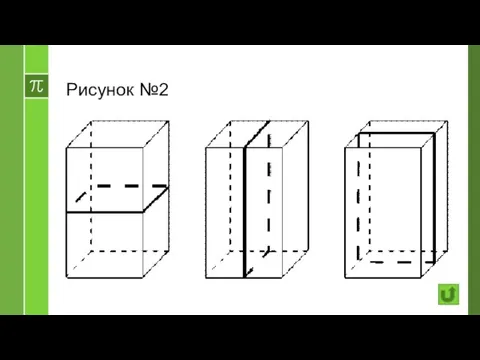
- 40. Рисунок №2
- 41. Рисунок №3
- 42. Пирамида многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми
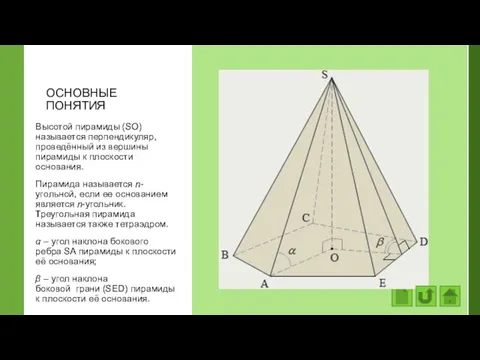
- 43. ОСНОВНЫЕ ПОНЯТИЯ Высотой пирамиды (SО) называется перпендикуляр, проведённый из вершины пирамиды к плоскости основания. Пирамида называется
- 44. Основание центр описанной окружности основание высоты пирамиды является центром окружности, описанной около основания пирамиды, тогда и
- 45. Основание центр вписанной окружности Основание высоты пирамиды является центром окружности, вписанной в основание пирамиды, тогда и
- 46. ПРАВИЛЬНАЯ ПИРАМИДА Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с
- 47. УСЕЧЕННАЯ ПИРАМИДА Плоскость, которая пересекает пирамиду и параллельна её основанию, делит её на две части: пирамиду,
- 48. ПРАВИЛЬНАЯ УСЕЧЕННАЯ ПИРАМИДА Усеченная пирамида (например, АВСDA1В1С1D1), которая получается из правильной пирамиды, также называется правильной. Боковые
- 49. Многоугольник это замкнутая линия, которая образовывается, если взять n каких-либо точек A1, A2, ..., An и
- 50. Определитель Простой определитель Способ столбцов и строк (ССС) Правило Саррюса Правило треугольника Что такое определитель? Для
- 51. Определитель матрицы. Определитель (детерминант) матрицы - выражение, составленное из матрицы, с помощью которого находят решение систем
- 52. Вычисление определителей
- 53. Вычисление определителя матрицы 3-го порядка
- 54. Правило Саррюса
- 55. Правило треугольника: значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках
- 56. Система координат комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или
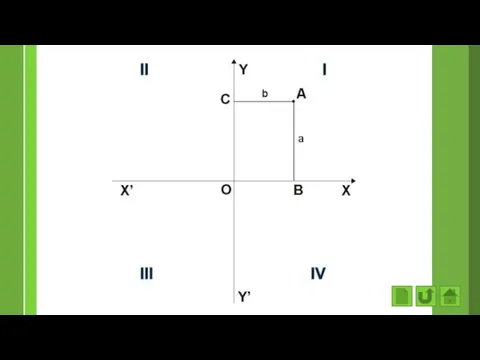
- 57. Прямоугольная система координат на плоскости(декартовая) образуется тремя взаимно перпендикулярными осями координат Ох(ось абсцисс) и Оу(ось ординат).
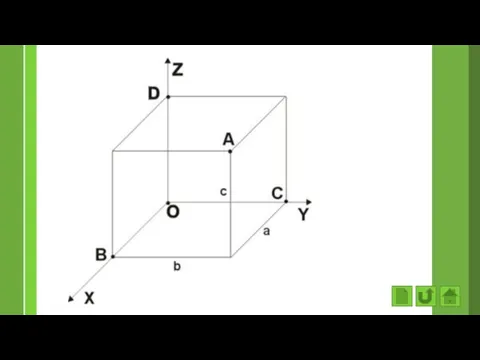
- 59. Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат Ох(ось абсцисс), Оу(ось ординат) и
- 61. Система это совокупность элементов или отношений, закономерно связанных друг с другом в единое целое.
- 62. Стереометрия отдел геометрии, изучающий фигуры, не лежащие в одной плоскости.
- 64. Скачать презентацию


















































 Прямоугольник
Прямоугольник Как лгать при помоощи статистики
Как лгать при помоощи статистики Интерполяционный многочлен Лагранжа
Интерполяционный многочлен Лагранжа Координатная плоскость
Координатная плоскость Производные тригонометрических функций. 10 класс
Производные тригонометрических функций. 10 класс Построение и анализ параллельных алгоритмов
Построение и анализ параллельных алгоритмов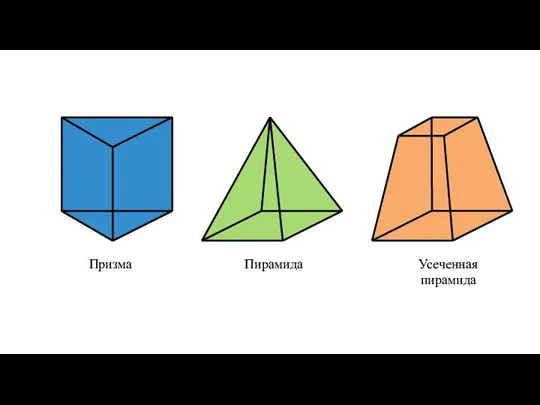 Симметрия. Виды симметрии
Симметрия. Виды симметрии Графики тригонометрических функций
Графики тригонометрических функций ГИА - 2018. Открытый банк заданий по математике. Задача №12
ГИА - 2018. Открытый банк заданий по математике. Задача №12 Тренажер вычисления производной
Тренажер вычисления производной Правильные многогранники
Правильные многогранники Массивы. Работа с массивами
Массивы. Работа с массивами Параллелограмм и трапеция. Урок 6
Параллелограмм и трапеция. Урок 6 Приемы устных вычислений в пределах 100. 3 класс
Приемы устных вычислений в пределах 100. 3 класс Однородные тригонометрические уравнения
Однородные тригонометрические уравнения 13_razn_dejstv_1
13_razn_dejstv_1 Сложение с переходом через десяток вида +8, +9. Считаем с гномами
Сложение с переходом через десяток вида +8, +9. Считаем с гномами Презентация на тему Фестиваль - КОМПЬЮТЕРНАЯ СТРАНА
Презентация на тему Фестиваль - КОМПЬЮТЕРНАЯ СТРАНА  Вычисление координат середины отрезка. Вычисление длины отрезка по его координатам. Вычисление расстояния между двумя точками
Вычисление координат середины отрезка. Вычисление длины отрезка по его координатам. Вычисление расстояния между двумя точками Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Презентация на тему Иррациональные числа (8 класс)
Презентация на тему Иррациональные числа (8 класс)  Преобразование графиков квадратичной функции. 8 класс
Преобразование графиков квадратичной функции. 8 класс Таблица умножения. Анимированная сорбонка
Таблица умножения. Анимированная сорбонка Решение геометрических задач. Треугольники
Решение геометрических задач. Треугольники Системы линейных уравнений с двумя переменными
Системы линейных уравнений с двумя переменными Свойства сложения
Свойства сложения Случаи вычитания 14 -
Случаи вычитания 14 - Площадь треугольника
Площадь треугольника