Содержание
- 2. ❤tt♣✿✴✴♠❛t❤❝②❜✳❝s✳♠s✉✳s✉
- 4. В простейших комбинаторных задачах требуется подсчитать число способов выбрать k элементов из n–элементного множества. То, что
- 5. Понятие выборки отличается от понятия подмножества: в выборках может допускаться повторение элементов, т.е. выборки могут быть
- 6. Упорядоченная (n, k)– выборка без повторений называется (n, k)– размещением (перестановкой) или размещением из n элементов
- 7. Например, рассмотрим множество A ={a1,a2,a3}. Составим выбор из трех элементов по два (3,2): Размещения - Повторения
- 8. Очень многие комбинаторные задачи решаются с помощью определения мощности множеств: равенства, суммы и произведения. Правило равенства.
- 11. Правило суммы: n(A∪B)=n(A)+n(B), n-мощность множеств n(A) - число элементов во множестве Пример: На одной полке книжного
- 13. Правило суммы Если элемент х может быть выбран k способами, а элемент у может быть выбран
- 14. Правило суммы – частный случай формулы включений и исключений. Если рассматривать А и B как множества
- 17. Задача 4. Сколько существует двузначных четных чисел с разными цифрами?
- 18. Задача 4. Сколько существует двузначных четных чисел с разными цифрами? Решение. Пусть α = α1α2 −
- 19. Задача 5. Сколько существует четырехзначных чисел, делящихся на 5, у которых все цифры различны?
- 24. А –первая буква французского слова arrangement, что означает размещение, приведение в порядок
- 26. Задача 5. Сколько различных четырехбуквенных «слов» можно составить, используя буквы а,f,c,o,n,e, если под «словом» понимать любую
- 29. P – первая буква французского слова permutation что означает перестановка
- 35. Размещение с повторениями из n элементов множества M по k - это всякая конечная последовательность, состоящая
- 40. Сколькими способами из колоды в 36 карт можно вытащить 5 карт так, чтобы среди них были
- 44. Сочетание с повторением С m n = С n n +m-1 В магазине есть 5 белых
- 46. Основные свойства сочетаний ФОРМУЛА СИММЕТРИИ ФОРМУЛА СЛОЖЕНИЯ ЧИСЛО ВСЕХ ПОДМНОЖЕСТВ N-ЭЛЕМЕНТНОГО МНОЖЕСТВА
- 48. Перестановки с повторениями Число различных перестановок, которые можно построить из n элементов, среди которых находятся n1
- 49. Число элементов в каждой перестановке равно Поэтому если бы все элементы были различны, то число перестановок
- 50. Например, в перестановке «ммаа» ничего не изменится, если переставит первый элемент со вторым, или третий с
- 52. ПРИМЕР: Сколько различных слов можно построить перестановкой букв в слове «лаваш»? Слово «лаваш» включает по одному
- 53. Задача. У врача 3 таблетки одного лекарства, 2 таблетки – другого и 4 таблетки – третьего.
- 54. Задача. Сколько различных слов можно получить перестановкой букв слова ОГОРОД так, чтобы три буквы "о" не
- 55. Найти количество перестановок букв в слове КОЛОБОК . В слове есть 3 буквы О и 2
- 57. Скачать презентацию






















































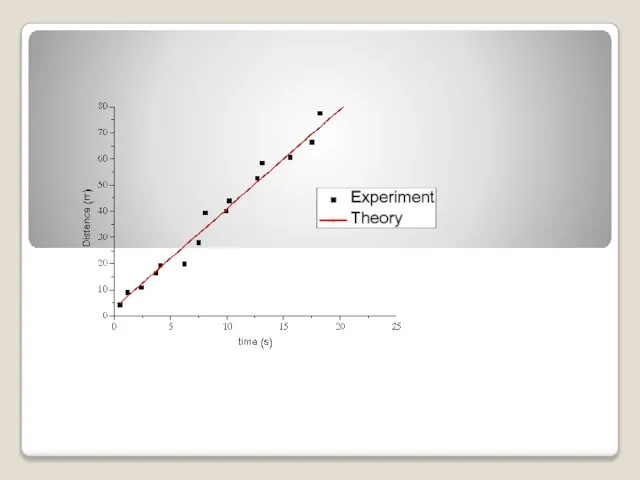 Планирование эксперимента. Логические основы
Планирование эксперимента. Логические основы Види кутів
Види кутів Презентация на тему Производная функции
Презентация на тему Производная функции  Счет
Счет Функции многих переменных
Функции многих переменных Призмы и антипризмы
Призмы и антипризмы Подготовка к контрольной работе. Уравнения
Подготовка к контрольной работе. Уравнения Презентация на тему Разложение многочленов на множители
Презентация на тему Разложение многочленов на множители  Умножение десятичных дробей
Умножение десятичных дробей Прямоугольный параллепипед. Итоговое повторение
Прямоугольный параллепипед. Итоговое повторение Положительные и отрицательные числа
Положительные и отрицательные числа Координатный метод в решении задач на плоскости Белобородова Н. Е., учитель математики МАОУ «СОШ №2»
Координатный метод в решении задач на плоскости Белобородова Н. Е., учитель математики МАОУ «СОШ №2» Наука статистика
Наука статистика Ряды распределения
Ряды распределения Перпендикулярность плоскостей. 10 класс
Перпендикулярность плоскостей. 10 класс L(q(x), h, H) шекаралық есептің меншікті мәндері және A(A) характеристикалық функцияның нөлдері
L(q(x), h, H) шекаралық есептің меншікті мәндері және A(A) характеристикалық функцияның нөлдері Арифметика в системах счисления
Арифметика в системах счисления Невозможный треугольник
Невозможный треугольник Осевая симметрия
Осевая симметрия Знакопостоянные числовые ряды. Лекция 1
Знакопостоянные числовые ряды. Лекция 1 Симметрия в пространстве
Симметрия в пространстве Решение различных задач с помощью систем уравнений второй степени
Решение различных задач с помощью систем уравнений второй степени Многоугольники в жизни
Многоугольники в жизни Периметр. Площа
Периметр. Площа Пространство IsR центрированных интервалов
Пространство IsR центрированных интервалов Основные тригонометрические тождества. Преобразование тригонометрических выражений
Основные тригонометрические тождества. Преобразование тригонометрических выражений Нормальные формы булевых функций
Нормальные формы булевых функций От землемерия к геометрии
От землемерия к геометрии