Содержание
- 2. Мнимая единица i – начальная буква французского слова imaginaire – «мнимый»
- 3. Например, Вычислите:
- 5. Значения степеней числа i повторяются с периодом, равным 4. Найдем:
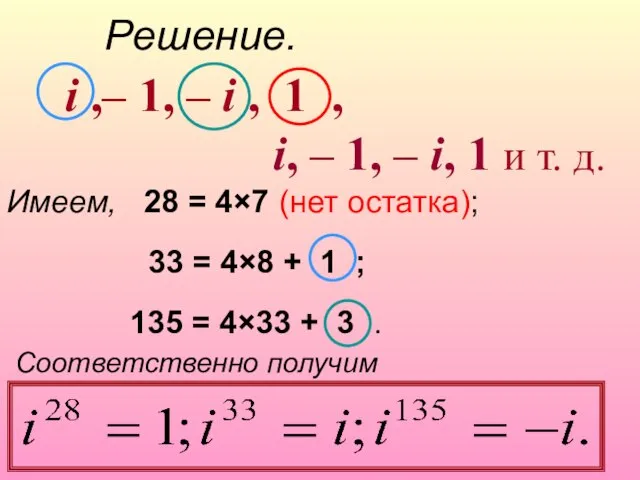
- 6. Решение. i ,– 1, – i , 1 , i, – 1, – i, 1 и
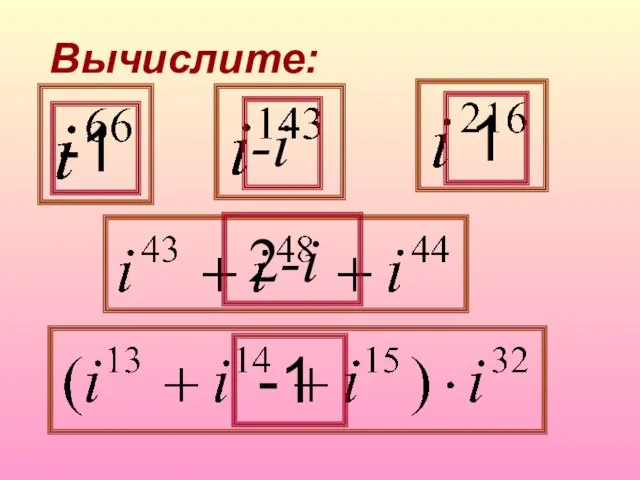
- 7. Вычислите: -1 -i 1 2-i -1
- 8. Комплексные числа Определение 1. Числа вида a + bi, где a и b – действительные числа,
- 9. VII в.н.э.- квадратный корень из положительного числа имеет два значения – положительное и отрицательное, а из
- 10. В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных
- 11. Он предложил Кордано назвал такие величины “чисто отрицательными” или даже “софистически отрицательными”, считая их бесполезными и
- 12. в 1572 году итальянский учёный Бомбелли выпустил книгу, в которой были установлены первые правила арифметических операций
- 13. Название “мнимые числа” ввёл французский математик и философ Р. Декарт в 1637 году
- 14. один из крупнейших математиков XVIII века – Л. Эйлер предложил использовать первую букву французского слова imaginare
- 15. гораздо В настоящее время в математике шире, комплексные числа используются действительные чем
- 16. Комплексные числа имеют прикладное значение во многих областях науки, являются основным аппаратом для расчетов в электротехнике
- 17. Применяются при конструировании ракет и самолетов
- 18. При вычерчивании географических карт
- 19. В исследовании течения воды, а также во многих других науках.
- 20. a + bi = c + di, если a = c и b = d. Определение
- 21. Решение. Согласно условию равенства комплексных чисел имеем 3y = 15, 5x = – 7. Отсюда Найти
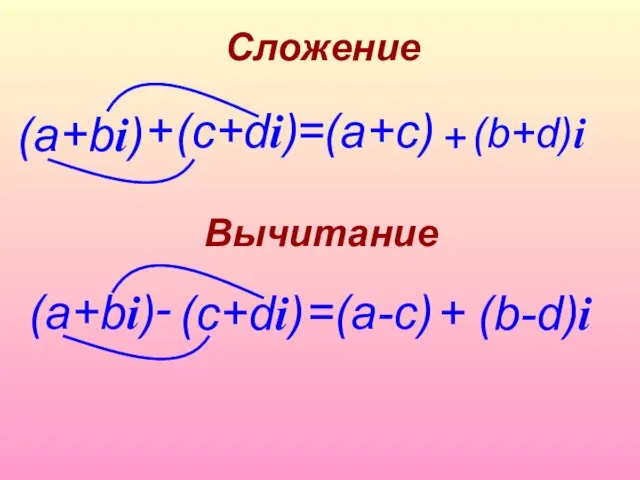
- 22. (а+bi) Вычитание =(a+c) + (c+di) Сложение (b+d) + i (а+bi) - (c+di) =(a-c) + (b-d) i
- 23. Выполните действия: z1 = 2 + 3i, z2 = 5 – 7i. Найти: а) z1 +
- 24. Умножение (c+di) = ac bс i = + + + аd bd (а+bi) i = =
- 25. Выполните действия: (5 + 3i)(5 – 3i) (2 + 3i)(5 – 7i) (2 – 7i)2 =
- 26. Определение 3. Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед
- 27. Деление = = =
- 28. Выполните действия: = = = 2
- 30. Скачать презентацию


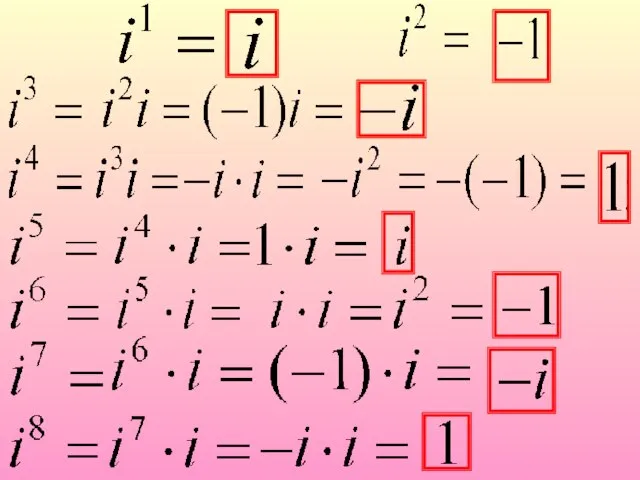





















 Презентация на тему Повторяем таблицу умножения
Презентация на тему Повторяем таблицу умножения  Деление на 2
Деление на 2 Научные открытия России. Задача тысячелетия. Теорема Пуанкаре
Научные открытия России. Задача тысячелетия. Теорема Пуанкаре Решение задач по теме Соотношения между сторонами и углами в прямоугольном треугольнике
Решение задач по теме Соотношения между сторонами и углами в прямоугольном треугольнике Тест для учащихся 1 класса
Тест для учащихся 1 класса Решение треугольников
Решение треугольников Презентация на тему Обозначение и сравнение углов
Презентация на тему Обозначение и сравнение углов  Лінійка — найпростіший прилад для вимірювання довжини
Лінійка — найпростіший прилад для вимірювання довжини Проверочная работа
Проверочная работа Презентация на тему РЕШЕНИЕ ЗАДАЧ ПО НАХОЖДЕНИЮ ВЕЛИЧИН ПО СУММЕ И РАЗНОСТИ
Презентация на тему РЕШЕНИЕ ЗАДАЧ ПО НАХОЖДЕНИЮ ВЕЛИЧИН ПО СУММЕ И РАЗНОСТИ  Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений 7 класс
7 класс Решение уравнений
Решение уравнений Легенды о Пифагоре и его теореме
Легенды о Пифагоре и его теореме Пригоди крапельки
Пригоди крапельки Длиннее, короче. Одинаковые по длине
Длиннее, короче. Одинаковые по длине Системы массового обслуживания
Системы массового обслуживания Презентация на тему ВТОРОЙ И ТРЕТИЙ ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ
Презентация на тему ВТОРОЙ И ТРЕТИЙ ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ  Презентация на тему Сумма и разность десятичных дробей
Презентация на тему Сумма и разность десятичных дробей  Математическая модель Память человека
Математическая модель Память человека Центральная симметрия относительно точки
Центральная симметрия относительно точки Презентация на тему Сложение положительных и отрицательных чисел
Презентация на тему Сложение положительных и отрицательных чисел  Разгадать ребус
Разгадать ребус Свойства тригонометрических функций
Свойства тригонометрических функций Ряд Тейлора функции многих переменных. Лекция 19
Ряд Тейлора функции многих переменных. Лекция 19 Физический и механический смысл производных. Использование производной в физике, механике
Физический и механический смысл производных. Использование производной в физике, механике Pakāpe ar naturālu kāpinātāju un tās Īpašība
Pakāpe ar naturālu kāpinātāju un tās Īpašība Площадь сферы
Площадь сферы