Выборка. Обобщение введенных понятий

Тема: Выборка.
Обобщение введенных понятий.
Цель лекции – изучить формулы представления и свойства биномиальных и полиномиальных коэффициентов

Литература
Глускин Л.М., Шор Л.А., Шварц В.Я. Задачи и алгоритмы комбинаторики, и теории графов. Донецк, ДПИ, 1982. 368 с.
Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике. М.: Наука, 1977. 368 с.
Ежов И.И., Скороход А.В., Ядренко М.И. Элементы комбинаторики: Пер. с укр. М.: Главная редакция физико-математической литературы издательства Наука, 1977. 80 с.
Виленкин Н.Я. Индукция. Комбинаторика. М.: Просвещение, 1976. 48 с.
Хаханов В.І., Хаханова І.В., Кулак Е.М., Чумаченко С.В. Методичні вказівки до практичних занять з курсу “Дискретна математика”. Харків, ХНУРЕ. 2001. С.67-70.

Базовые понятия:
Множество
Бином
Биномиальные коэффициенты и формула для них
Перестановка
Термины
Ключевые слова:
Сочетание
Размещение
Сочетание и размещение с повторением
Выборка

ПРИМЕР 1
Дано множество M={a,b,c}
Перестановки с повторениями из 3 элементов по 2:
{a,b,c}×{a,b,c}={ (a,a), (a,b), (a,c), (b,a), (b,b), (b,c), (c,a), (c,b), (c,c)}, их количество nk=32=9
Перестановки без повторений из 3 элементов по 2 ≡ упорядоченные сочетания без повторений ≡ размещения из трех элементов по 2:
{ (a,b), (a,c), (b,a), (b,c), (c,a), (c,b) }, их количество

ПРИМЕР 2
Дано множество M={a,b,c}
Сочетания без повторений из 3 элементов по 2 :
{a,b}, {a,c}, {b,c}, их количество
Сочетания с повторениями из 3 элементов по 2:
{a,a}, {a,b}, {a,c}, {b,b}, {b,c}, {c,c}, их количество

N-МЕРНЫЙ КУБ
Вершины n-мерного куба можно рассматривать как совокупность упорядоченных сочетаний с повторениями (размещений с повторениями) из элементов множества Ek={0,1,2,…, k-1} по n:

КОМБИНАТОРНАЯ МЕРА ИНФОРМАЦИИ
В комбинаторной мере информации количество информации определяется как число комбинаций элементов (сочетаний символов).
Количество информации совпадает с числом возможных сочетаний, перестановок и размещений элементов.
Комбинирование символов в словах, состоящих только из 0 и 1, меняет значения слов.
Рассмотрим две пары слов:
100110 и 001101;
011101 и 111010.
В них произведена перестановка крайних разрядов (изменено местоположение знакового разряда в числе – перенесен слева направо).

ВЕРОЯТНОСТЬ ИСКАЖЕНИЯ ИНФОРМАЦИИ
В теории кодирования имеет место понятие вероятности искажения информации.
Понятие корректирующей способности кода обычно связывают с возможностью обнаружения и исправления ошибки. Количественно корректирующая способность кода определяется вероятностью обнаружения или исправления ошибки.
Пусть имеется n-разрядный код и вероятность искажения одного символа равна p. Количество кодовых комбинаций, каждая из которых содержит k искажений символов, равна числу сочетаний из n по k:
Вероятность того, что искажены k символов, а остальные n-k символов не искажены, определяется как
pk(1-p)n-k
Полная вероятность искажения информации определяется как

TIME-OUT

ВЫБОРКА.
СИСТЕМАТИЗАЦИЯ КОМБИНАТОРНЫХ ПОНЯТИЙ. 1
Def: набор элементов из множества называется выборкой объема k из n элементов или (n.k)-выборкой
Def: выборка называется упорядоченной, если в ней задан порядок следования элементов
Две упорядоченные выборки считаются различными, если они отличаются лишь порядком следования элементов
В выборках могут допускаться повторения элементов
Def: упорядоченная (n,k)-выборка, в которой элементы могут повторяться, называется перестановкой с повторениями из n элементов по k или (n,k)-перестановкой с повторениями
Число (n,k)-перестановок с повторениями определяется как nk
Def: если элементы упорядоченной (n,k)-выборки попарно различны, то она называется (n,k)-перестановкой без повторений или просто (n,k)-перестановкой
Число (n,k)-перестановок без повторений определяется как n!

ВЫБОРКА.
СИСТЕМАТИЗАЦИЯ КОМБИНАТОРНЫХ ПОНЯТИЙ. 2
Def: неупорядоченная (n,k)-выборка, в которой элементы могут повторяться, называется сочетанием с повторениями из n элементов по k или (n,k)-сочетанием с повторениями.
Число сочетаний с повторениями из n элементов по k определяется как
Def: если элементы неупорядоченной выборки попарно различны, то она называется сочетанием без повторений из n элементов по k или (n,k)-сочетанием. Каждое такое сочетание представляет подмножество мощности k
Число сочетаний без повторений из n элементов по k определяется как

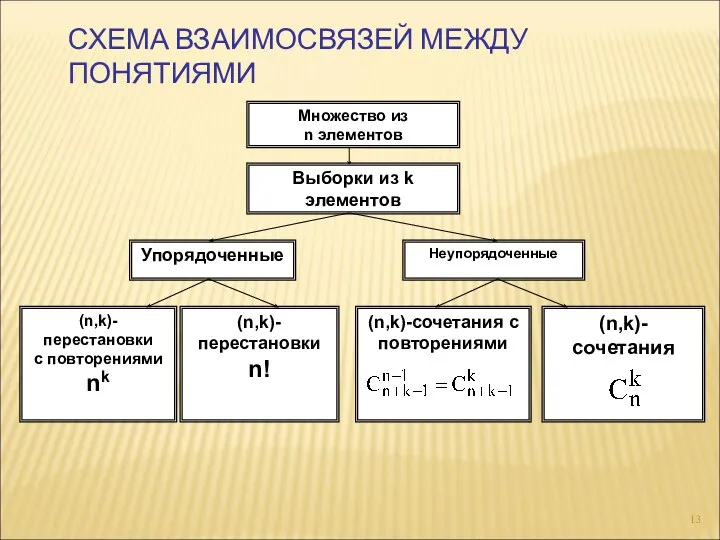
СХЕМА ВЗАИМОСВЯЗЕЙ МЕЖДУ ПОНЯТИЯМИ

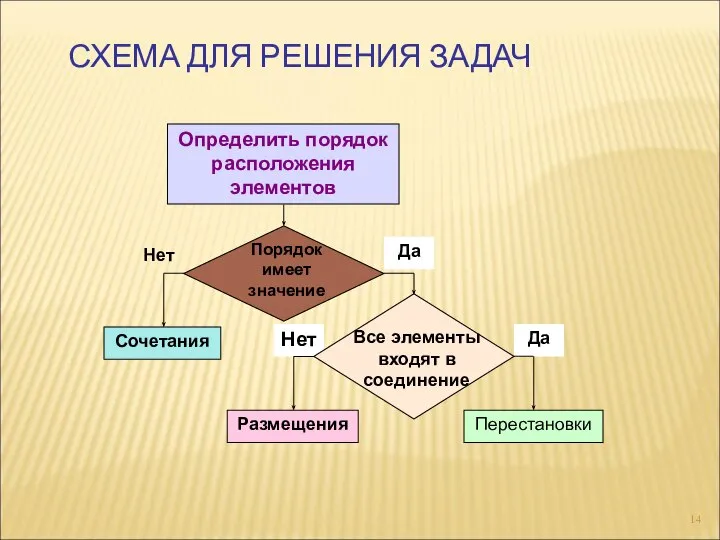
СХЕМА ДЛЯ РЕШЕНИЯ ЗАДАЧ

ТЕСТ-ВОПРОСЫ. 1
1. Что является более общим понятием:
а) перестановки;
б) размещения;
в) сочетания.
2. В каком случае мощность множества больше:
а) в размещении без повторений;
б) в размещении с повторениями;
в) одинаково.
3. В каком случае мощность множества больше:
а) в перестановках без повторений;
б) в перестановках с повторениями;
в) одинаково.