Метод комплексных амплитуд при моделировании радиосистем. Лекция 12

Литература
Борисов Ю.П., Цветнов В.В. Математическое моделирование радиотехнических систем и устройств. - М.: Радио и связь, 1985. 176 с.
Глава 5. Метод комплексной огибающей

Амплитуда и фаза
Что есть амплитуда и фаза сигнала?
Со школьной скамьи эти понятия неразрывно связаны с гармоническим колебанием:
– амплитуда
– начальная фаза
– полная фаза
Эти понятия мы распространили на описание сигналов:
– «амплитуда»
– «фаза»
– полная фаза
– «амплитудный множитель», «огибающая»

Преобразование Гильберта
А как быть с произвольным вещественным сигналом ?
Ему можно сопоставить комплексный аналитический сигнал
с помощью преобразования Гильберта:
Преобразование Гильберта – ответ на вопрос:
тогда ИХ фильтра, формирующего ортогональный сигнал
– ядро преобразования Гильберта

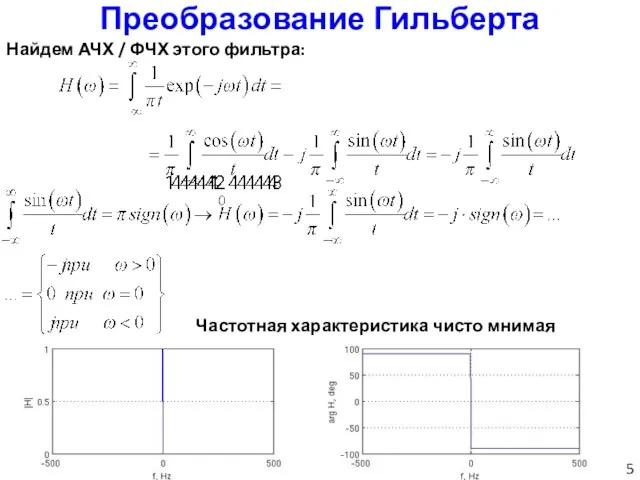
Преобразование Гильберта
Найдем АЧХ / ФЧХ этого фильтра:
Частотная характеристика чисто мнимая

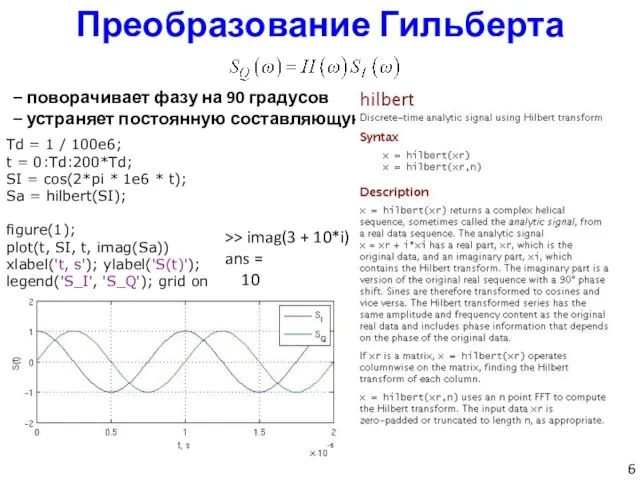
Преобразование Гильберта
– поворачивает фазу на 90 градусов
– устраняет постоянную составляющую.
Td = 1 / 100e6;
t = 0:Td:200*Td;
SI = cos(2*pi * 1e6 * t);
Sa = hilbert(SI);
figure(1);
plot(t, SI, t, imag(Sa))
xlabel('t, s'); ylabel('S(t)');
legend('S_I', 'S_Q'); grid on
>> imag(3 + 10*i)
ans =
10

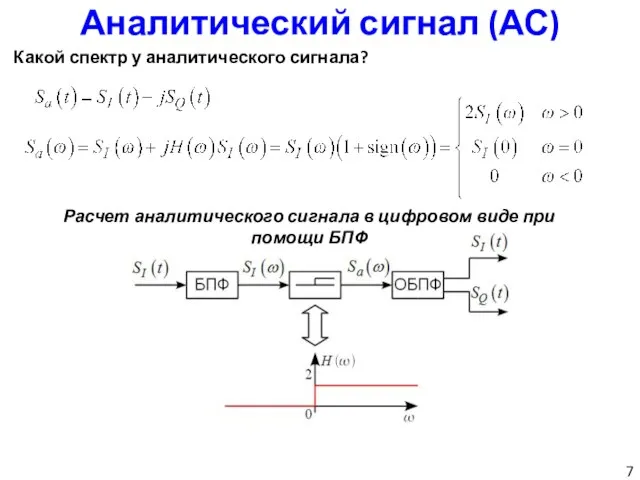
Аналитический сигнал (АС)
Какой спектр у аналитического сигнала?
Расчет аналитического сигнала в цифровом виде при помощи БПФ

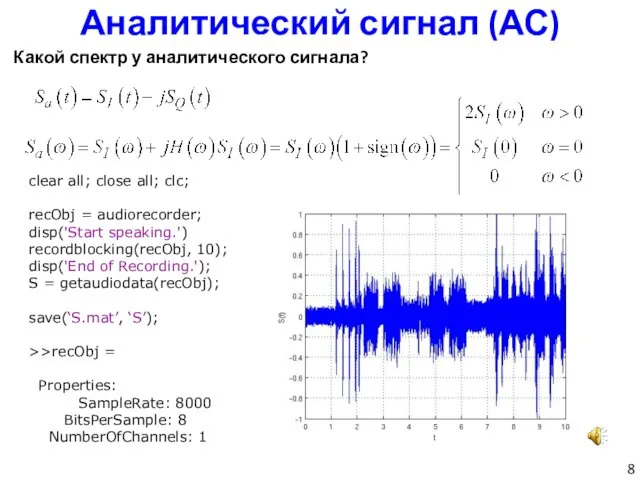
Аналитический сигнал (АС)
Какой спектр у аналитического сигнала?
clear all; close all; clc;
recObj = audiorecorder;
disp('Start speaking.')
recordblocking(recObj, 10);
disp('End of Recording.');
S = getaudiodata(recObj);
save(‘S.mat’, ‘S’);
>>recObj =
Properties:
SampleRate: 8000
BitsPerSample: 8
NumberOfChannels: 1

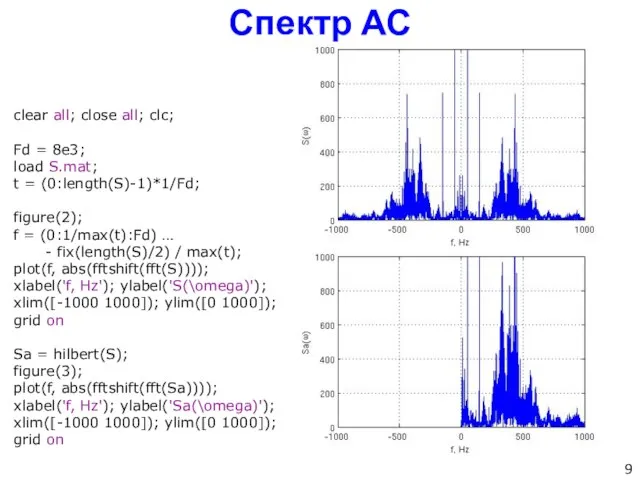
Спектр АС
clear all; close all; clc;
Fd = 8e3;
load S.mat;
t = (0:length(S)-1)*1/Fd;
figure(2);
f = (0:1/max(t):Fd) …
- fix(length(S)/2) / max(t);
plot(f, abs(fftshift(fft(S))));
xlabel('f, Hz'); ylabel('S(\omega)');
xlim([-1000 1000]); ylim([0 1000]);
grid on
Sa = hilbert(S);
figure(3);
plot(f, abs(fftshift(fft(Sa))));
xlabel('f, Hz'); ylabel('Sa(\omega)');
xlim([-1000 1000]); ylim([0 1000]);
grid on

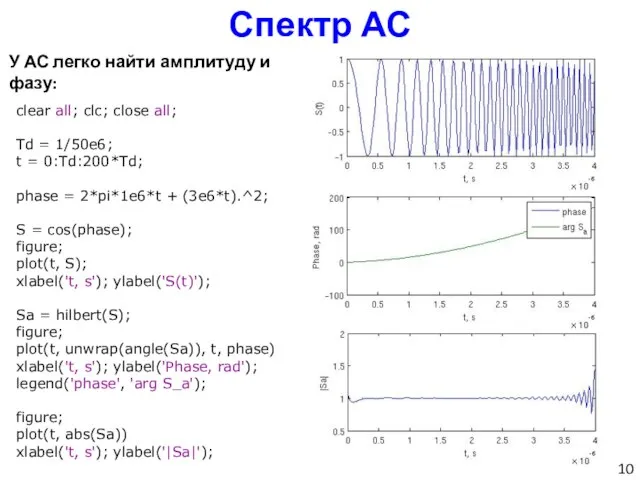
Спектр АС
clear all; clc; close all;
Td = 1/50e6;
t = 0:Td:200*Td;
phase = 2*pi*1e6*t + (3e6*t).^2;
S = cos(phase);
figure;
plot(t, S);
xlabel('t, s'); ylabel('S(t)');
Sa = hilbert(S);
figure;
plot(t, unwrap(angle(Sa)), t, phase)
xlabel('t, s'); ylabel('Phase, rad');
legend('phase', 'arg S_a');
figure;
plot(t, abs(Sa))
xlabel('t, s'); ylabel('|Sa|');
У АС легко найти амплитуду и фазу:

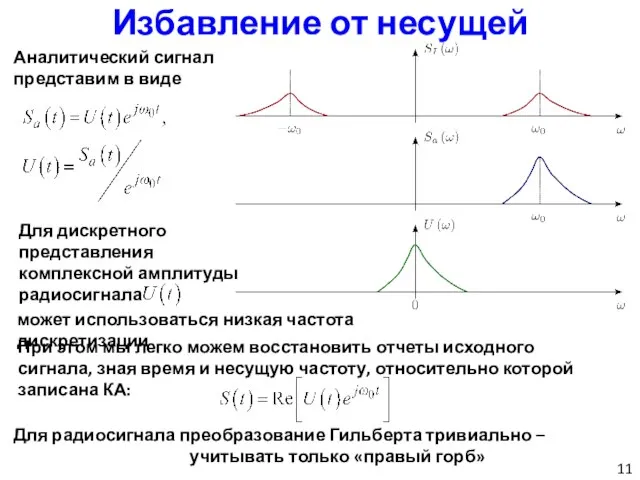
Избавление от несущей
Аналитический сигнал представим в виде
Для дискретного
представления
комплексной амплитуды
радиосигнала
может использоваться низкая частота дискретизации
При этом мы легко можем восстановить отчеты исходного сигнала, зная время и несущую частоту, относительно которой записана КА:
Для радиосигнала преобразование Гильберта тривиально –
учитывать только «правый горб»

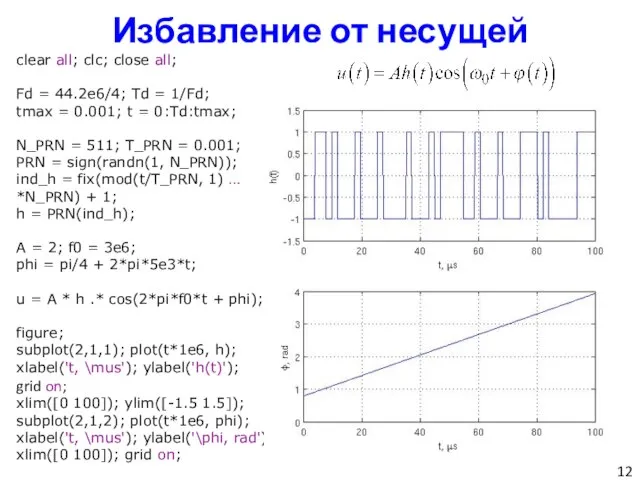
Избавление от несущей
clear all; clc; close all;
Fd = 44.2e6/4; Td = 1/Fd;
tmax = 0.001; t = 0:Td:tmax;
N_PRN = 511; T_PRN = 0.001;
PRN = sign(randn(1, N_PRN));
ind_h = fix(mod(t/T_PRN, 1) …
*N_PRN) + 1;
h = PRN(ind_h);
A = 2; f0 = 3e6;
phi = pi/4 + 2*pi*5e3*t;
u = A * h .* cos(2*pi*f0*t + phi);
figure;
subplot(2,1,1); plot(t*1e6, h);
xlabel('t, \mus'); ylabel('h(t)');
grid on;
xlim([0 100]); ylim([-1.5 1.5]);
subplot(2,1,2); plot(t*1e6, phi);
xlabel('t, \mus'); ylabel('\phi, rad')
xlim([0 100]); grid on;

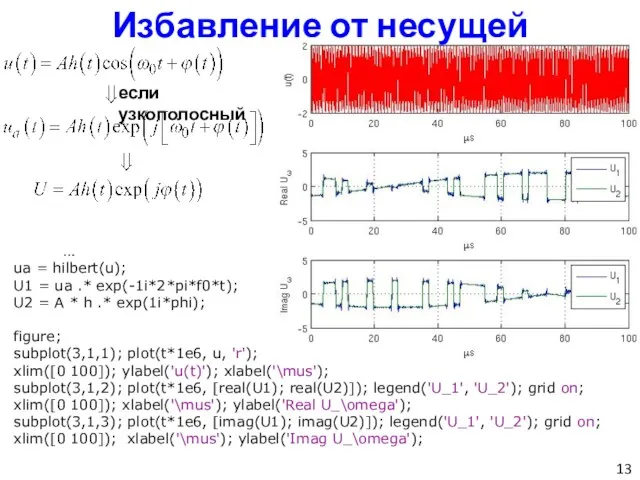
Избавление от несущей
…
ua = hilbert(u);
U1 = ua .* exp(-1i*2*pi*f0*t);
U2 = A * h .* exp(1i*phi);
figure;
subplot(3,1,1); plot(t*1e6, u, 'r');
xlim([0 100]); ylabel('u(t)'); xlabel('\mus');
subplot(3,1,2); plot(t*1e6, [real(U1); real(U2)]); legend('U_1', 'U_2'); grid on;
xlim([0 100]); xlabel('\mus'); ylabel('Real U_\omega');
subplot(3,1,3); plot(t*1e6, [imag(U1); imag(U2)]); legend('U_1', 'U_2'); grid on;
xlim([0 100]); xlabel('\mus'); ylabel('Imag U_\omega');
если узкополосный

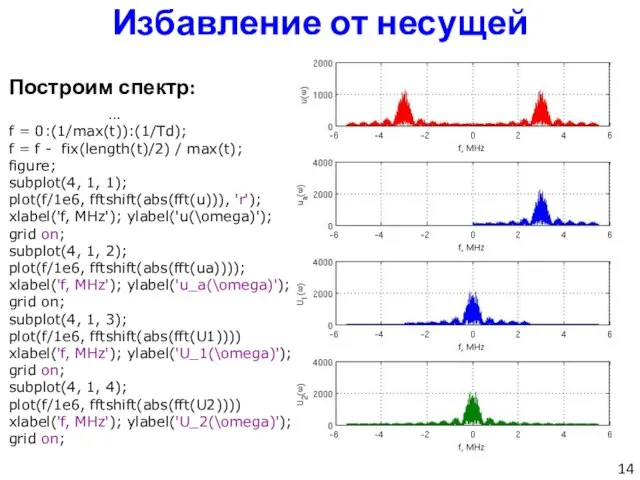
Избавление от несущей
Построим спектр:
…
f = 0:(1/max(t)):(1/Td);
f = f - fix(length(t)/2) / max(t);
figure;
subplot(4, 1, 1);
plot(f/1e6, fftshift(abs(fft(u))), 'r');
xlabel('f, MHz'); ylabel('u(\omega)');
grid on;
subplot(4, 1, 2);
plot(f/1e6, fftshift(abs(fft(ua))));
xlabel('f, MHz'); ylabel('u_a(\omega)');
grid on;
subplot(4, 1, 3);
plot(f/1e6, fftshift(abs(fft(U1))))
xlabel('f, MHz'); ylabel('U_1(\omega)');
grid on;
subplot(4, 1, 4);
plot(f/1e6, fftshift(abs(fft(U2))))
xlabel('f, MHz'); ylabel('U_2(\omega)');
grid on;

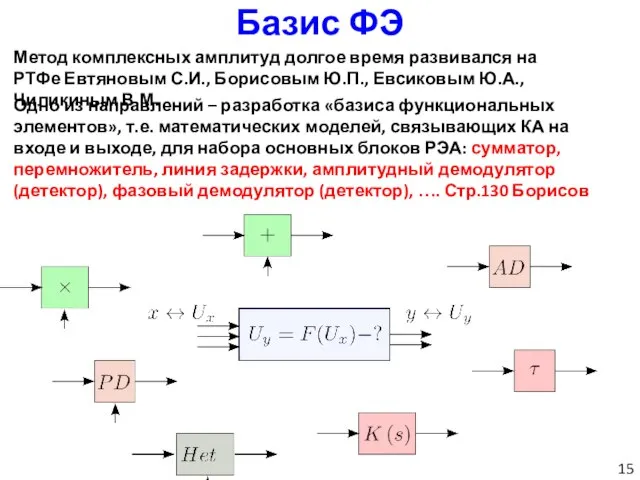
Базис ФЭ
Метод комплексных амплитуд долгое время развивался на РТФе Евтяновым С.И., Борисовым Ю.П., Евсиковым Ю.А., Чиликиным В.М.
Одно из направлений – разработка «базиса функциональных элементов», т.е. математических моделей, связывающих КА на входе и выходе, для набора основных блоков РЭА: сумматор, перемножитель, линия задержки, амплитудный демодулятор (детектор), фазовый демодулятор (детектор), …. Стр.130 Борисов

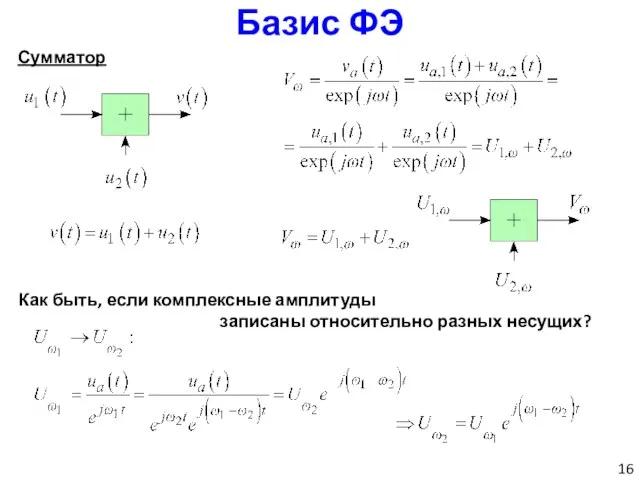
Базис ФЭ
Сумматор
Как быть, если комплексные амплитуды
записаны относительно разных несущих?

Базис ФЭ
Умножитель
Если медленно меняется
Иначе всё усложняется

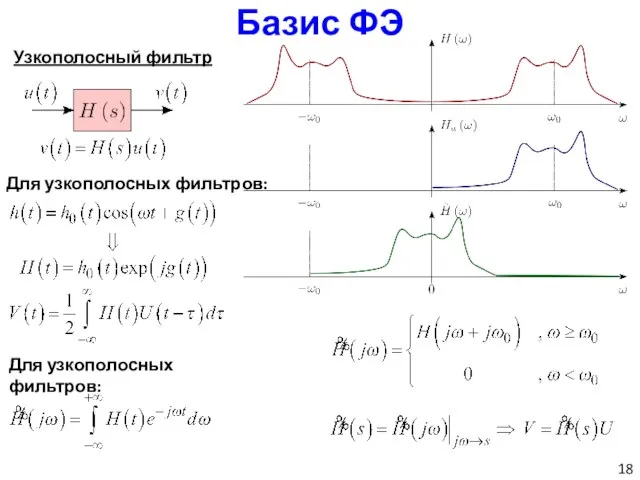
Базис ФЭ
Узкополосный фильтр
Для узкополосных фильтров:
Для узкополосных фильтров:

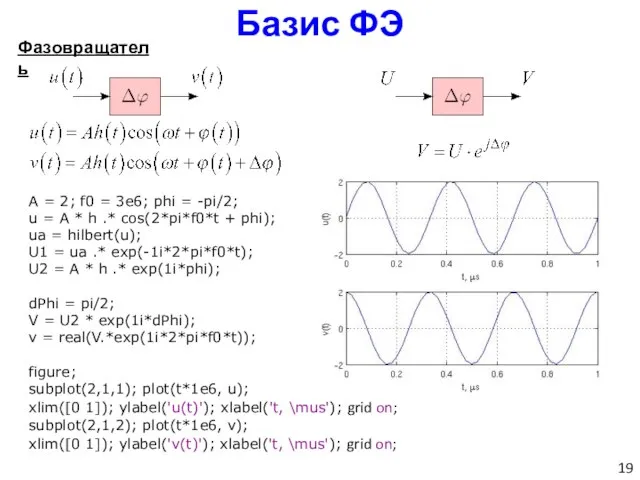
Базис ФЭ
Фазовращатель
A = 2; f0 = 3e6; phi = -pi/2;
u = A * h .* cos(2*pi*f0*t + phi);
ua = hilbert(u);
U1 = ua .* exp(-1i*2*pi*f0*t);
U2 = A * h .* exp(1i*phi);
dPhi = pi/2;
V = U2 * exp(1i*dPhi);
v = real(V.*exp(1i*2*pi*f0*t));
figure;
subplot(2,1,1); plot(t*1e6, u);
xlim([0 1]); ylabel('u(t)'); xlabel('t, \mus'); grid on;
subplot(2,1,2); plot(t*1e6, v);
xlim([0 1]); ylabel('v(t)'); xlabel('t, \mus'); grid on;