Многогранники. Стереометрия

Введение
Стереометрия – раздел геометрии, в котором изучают свойства фигур в пространстве.
Предметы стереометрии:
•Точки
•Прямые
•Плоскости
•Геометрические тела и их поверхности

Многогранник – поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.
Грани– многоугольники, из которых состоит многогранник.
Ребра – стороны граней.
Вершины – концы рёбер.
Диагонали – отрезки, соединяющие две вершины, не принадлежащие одной грани.

Многогранники бывают выпуклые и невыпуклые. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
Примеры выпуклых и невыпуклых многогранников

Теорема Эйлера
В любом выпуклом многограннике сумма числа граней и числа вершин больше числа ребер на 2

Правильный многогранник
Правильный многогранник – выпуклый многогранник, гранями которого являются правильные многоугольники.

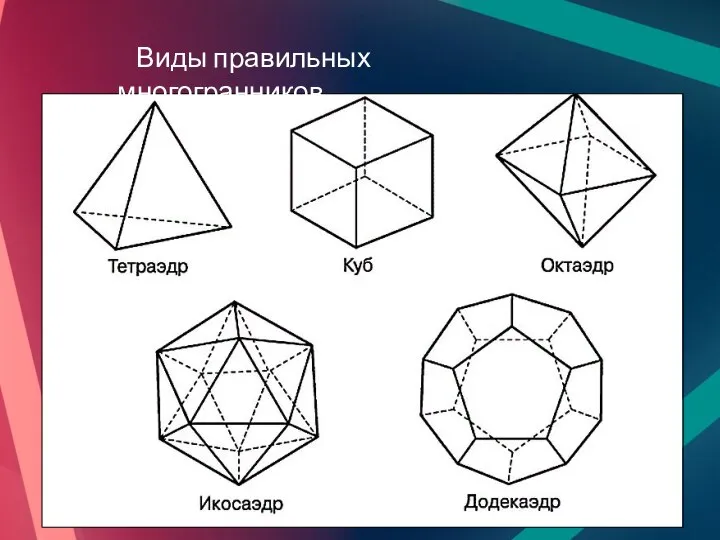
Виды правильных многогранников

Призма – многогранник, основания которого являются равными многоугольниками, а боковые стороны – параллелограммами.
Призма

Пирамида – многогранник, основание которого является произвольный многоугольник, а боковые грани – треугольники, имеющие общую вершину
Пирамида

Формулы для нахождения объёма и площади поверхности некоторых многогранников

Задача 1
Найдите объем куба, если площадь его поверхности равна 54.

Решение

Задача 2
Площадь поверхности прямоугольного параллелепипеда равна 16 . Найдите его диагональ, если два ребра равны 1 и 2 .

Решение
Площадь поверхности можно найти по формуле . Значит, . Тогда диагональ .

Внимание!