- Главная
- Математика
- О подобии произвольных фигур

Содержание
Слайд 2UROKIMATEMATIKI.RU
Игорь Жаборовский © 2012
k – КОЭФФИЦИЕНТ ПОДОБИЯ фигур F и F1
фигуры F
UROKIMATEMATIKI.RU
Игорь Жаборовский © 2012
k – КОЭФФИЦИЕНТ ПОДОБИЯ фигур F и F1
фигуры F

и F1 называются ПОДОБНЫМИ, если каждой точке фигуры F можно сопоставить точку фигуры F1 так,
что для любых двух точек М и N фигуры F и сопоставленных им точек М1 и N1 фигуры F1
выполняется равенство ,
где k – одно и то же положительное число для всех точек
Слайд 3UROKIMATEMATIKI.RU
Игорь Жаборовский © 2012
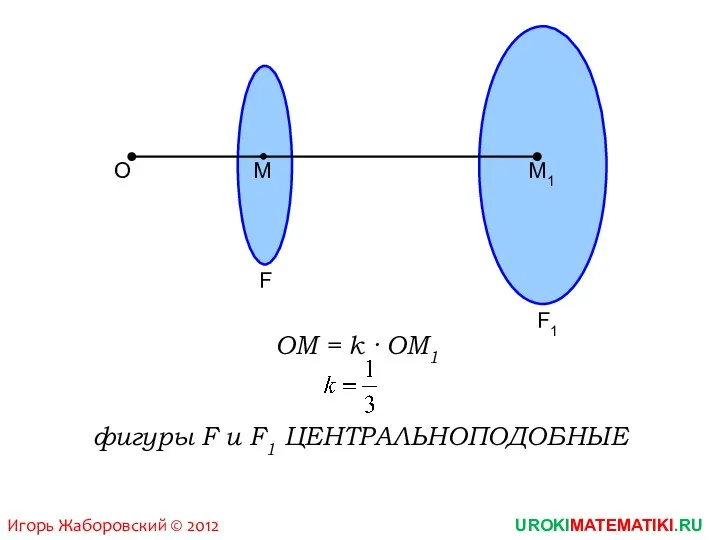
OM = k · OM1
F
F1
O
M
M1
фигуры F и F1 ЦЕНТРАЛЬНОПОДОБНЫЕ
UROKIMATEMATIKI.RU
Игорь Жаборовский © 2012
OM = k · OM1
F
F1
O
M
M1
фигуры F и F1 ЦЕНТРАЛЬНОПОДОБНЫЕ
- Предыдущая
Potrebnost_dvizheniaСледующая -
Нарушения ритма и проводимости Задачи на готовых чертежах. Ромб
Задачи на готовых чертежах. Ромб Графическая лаборатория Цель: систематизировать знания по теме «Функции и их графики», закрепить навыки работы с графиками функц
Графическая лаборатория Цель: систематизировать знания по теме «Функции и их графики», закрепить навыки работы с графиками функц Сложение и вычитание десятичных дробей. 18 февраля в истории Кубани
Сложение и вычитание десятичных дробей. 18 февраля в истории Кубани Арифметический корень натуральной степени
Арифметический корень натуральной степени Числовые ряды
Числовые ряды Этапы создания математических моделей
Этапы создания математических моделей Интерактивная мозаика. Математические тесты
Интерактивная мозаика. Математические тесты VSM_mag_2-16
VSM_mag_2-16 Мультиколлинеарность – это взаимное влияние факторов друг на друга
Мультиколлинеарность – это взаимное влияние факторов друг на друга Контрольная работа по математике
Контрольная работа по математике Гарри Потер. Игра по математике и физике
Гарри Потер. Игра по математике и физике Производная сложной функции
Производная сложной функции Тригонометрия в различных областях науки и жизни
Тригонометрия в различных областях науки и жизни Многогранники в архитектуре
Многогранники в архитектуре Бесконечно убывающая геометрическая прогрессия
Бесконечно убывающая геометрическая прогрессия Найдите высоту и медиану треугольника
Найдите высоту и медиану треугольника Математическая викторина. Клуб Эрудит
Математическая викторина. Клуб Эрудит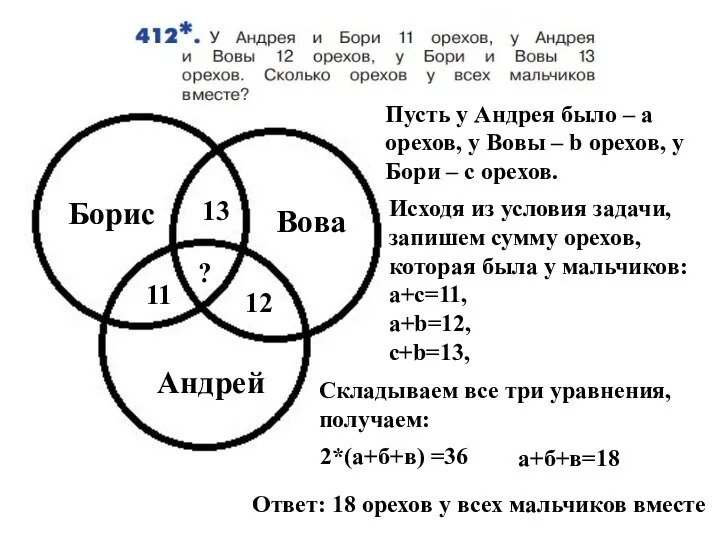 Уравнения. Задача
Уравнения. Задача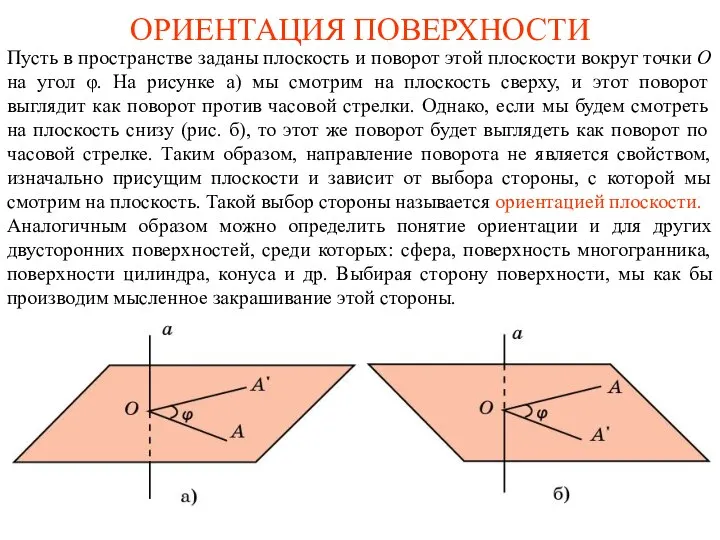 Ориентация поверхности. Лист Мёбиуса
Ориентация поверхности. Лист Мёбиуса Преобразование логарифмических выражений
Преобразование логарифмических выражений Простейшие уравнения
Простейшие уравнения Тренировочные варианты
Тренировочные варианты Решение задач с помощью уравнений
Решение задач с помощью уравнений Презентация на тему Решение задач с помощью рациональных уравнений (8 класс)
Презентация на тему Решение задач с помощью рациональных уравнений (8 класс)  Задача по математике (1 класс)
Задача по математике (1 класс) Геометрия. Что значит это слово? часть 1
Геометрия. Что значит это слово? часть 1 Площади. Тест 8 класс
Площади. Тест 8 класс Карта треугольника
Карта треугольника