Содержание
- 2. Летучка (ПИШЕМ ТОЛЬКО ОТВЕТЫ НА ВОПРОСЫ!) 1) 2) 3) 4) 5) Матрица – это… Определитель матрицы
- 3. Летучка(ОТВЕТЫ) 1) 2) 3) 4) 5) Матрица – это прямоугольная таблица чисел. Определитель матрицы –это число,
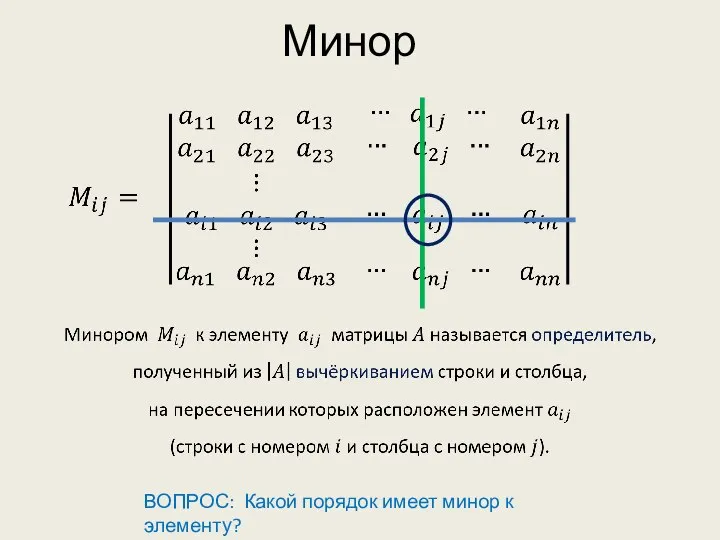
- 4. Минор ВОПРОС: Какой порядок имеет минор к элементу?
- 5. Пример 1.
- 6. Алгебраическое дополнение
- 7. Пример 2.
- 8. Пример 3.
- 9. Разложение определителя Удобно раскладывать определитель по строке, содержащей много нулей. (почему?)
- 10. Пример разложения определителя по строке: Пример разложения определителя по столбцу:
- 11. Обратная матрица Обратная матрица обозначается: Только у квадратной матрицы существует обратная. (почему?) ; по определению верно:
- 12. Построение обратной матрицы (Как в этом убедиться?)
- 13. Пример построения обратной матрицы 1)
- 14. 2) 3)
- 15. 4) 5) Дома сделать проверку.
- 16. Решение систем уравнений с помощью обратной матрицы Запишем систему линейных уравнений: с помощью матриц: Тогда система
- 17. По определению обратной матрицы , поэтому так как при умножении на единичную матрица не изменяется, то
- 18. Пример решения системы с помощью обратной матрицы
- 20. Скачать презентацию


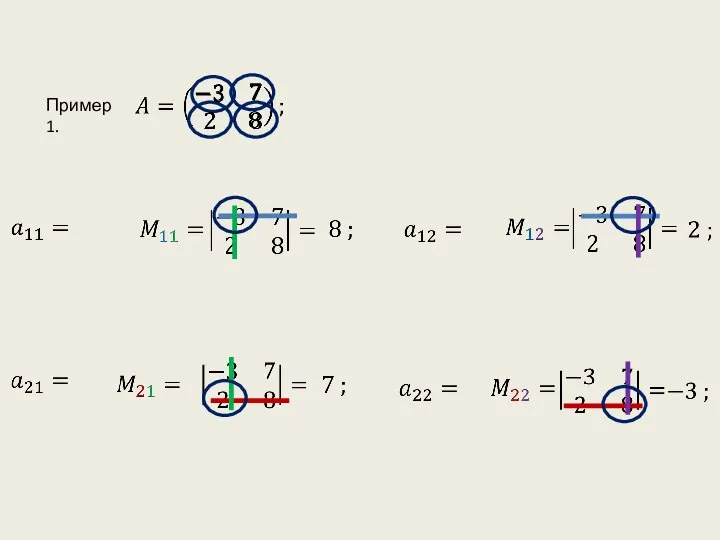

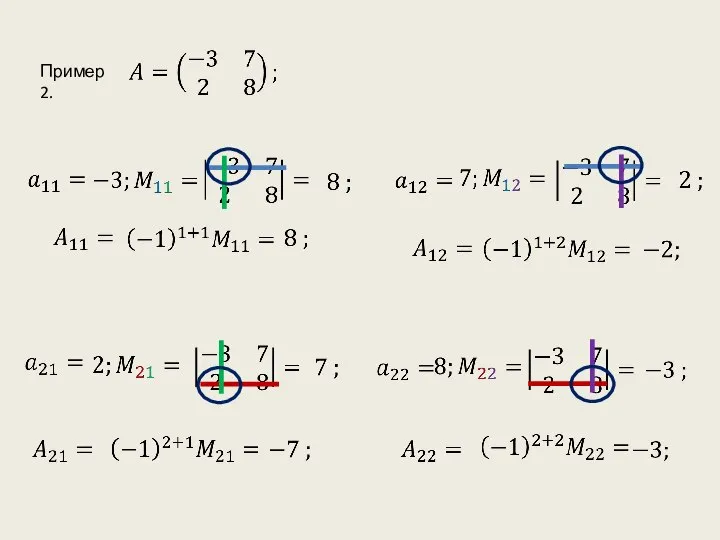
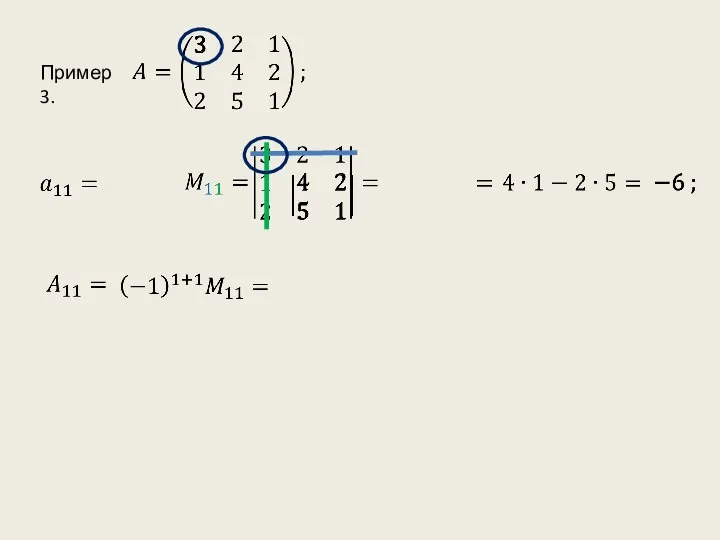





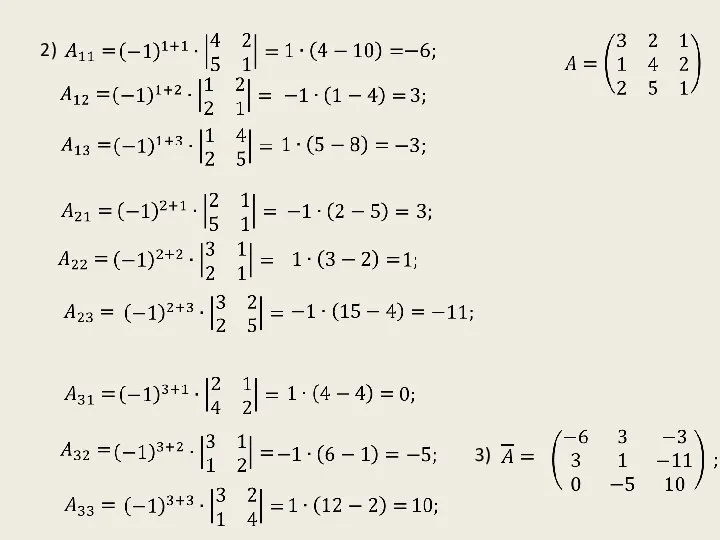




 Викторина по математике: Где логика?
Викторина по математике: Где логика? Призма
Призма Старинная задача по математике
Старинная задача по математике Элементы круга и окружности в задачах ОГЭ
Элементы круга и окружности в задачах ОГЭ Задачи и примеры по математике
Задачи и примеры по математике Интерактивные тренинги по математике для подготовки к ЕГЭ
Интерактивные тренинги по математике для подготовки к ЕГЭ Правила дифференцирования
Правила дифференцирования Типи трикутників
Типи трикутників Приведение к каноническому виду уравнений параболического типа
Приведение к каноническому виду уравнений параболического типа Доли. 3 класс
Доли. 3 класс Вынесение общего множителя за скобки. 6 класс
Вынесение общего множителя за скобки. 6 класс Презентация на тему Решение квадратных уравнений и неравенств
Презентация на тему Решение квадратных уравнений и неравенств  Классы Фиттинга с заданными свойствами операторов Локетта
Классы Фиттинга с заданными свойствами операторов Локетта Найдите производную функции. Практическая работа
Найдите производную функции. Практическая работа Геометрические приложения определенного интеграла
Геометрические приложения определенного интеграла user_file_5edd0051b6aa7
user_file_5edd0051b6aa7 Геометрия Евклида, как первая научная система
Геометрия Евклида, как первая научная система Фильтр Ходрика-Прескотта
Фильтр Ходрика-Прескотта Задания по математике
Задания по математике Строение функции, свойства, графики
Строение функции, свойства, графики Матрицы. Виды матриц
Матрицы. Виды матриц Применение производной к исследованию функции и построению графика функции
Применение производной к исследованию функции и построению графика функции Математика в Архітектурі
Математика в Архітектурі Задача о расшивке узких мест производства
Задача о расшивке узких мест производства Двоичная арифметика
Двоичная арифметика Правильные многогранникик
Правильные многогранникик Презентация на тему Математика. Единицы площади
Презентация на тему Математика. Единицы площади  Действительный анализ. Интеграл Римана и критерий Лебега
Действительный анализ. Интеграл Римана и критерий Лебега