Слайд 2Геометрическая интерпретация
|а| означает расстояние на координатной прямой от точки, изображающей число а,

до начала отсчета.
Если а 0, то на координатной прямой существует две точки а и –а, равноудаленные от нуля, модули которых равны.
Если а=0, то на координатной прямой |а| изображается точкой 0.
Слайд 3Пример 1. Решить неравенство:
Решение.
Рассмотрим четыре случая.
1) 3)
2) 4)
Объединим эти решения:

Слайд 4Пример 2. Решить уравнение:
Решение. Пусть . Тогда уравнение примет вид .

Воспользуемся геометрическим смыслом модуля: найдем все точки числовой оси, сумма расстояний от каждой из которых до точек 0 и 4 равна 10.
Ответ: {-4, -2, 1, 3}
Слайд 5Пример 3: Решить уравнение:
Решение: Уравнение равносильно следующему:
Пусть t =|x-2|, t

≥ 0. Тогда , и уравнение примет вид:
Но t ≥ 0, поэтому t = 1, откуда
Ответ: {1, 3}
Слайд 6Пример 4. Решить уравнение (неравенство):
а)
б)
в)
г)
д)

Слайд 7Решение: а) Так как обе части неравенства неотрицательны, то возведение в квадрат

является равносильным преобразование:
а)
Решим последнее неравенство методом интервалов:
Ответ:
Слайд 9в)
Решим второе неравенство последней совокупности методом интервалов:
Объединяя найденные решения с решением

неравенства , получим ответ.
Ответ:
Слайд 10г)
(1)
(2)
Решим (1) методом интервалов:
Решим (2) методом интервалов:
Найдем пересечение
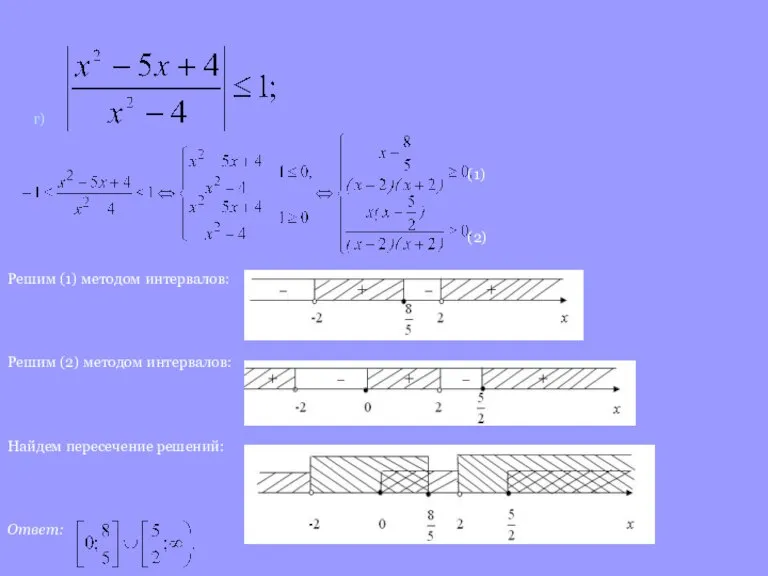
решений:
Ответ:
Слайд 11д)
Перепишем уравнение (так как |-a|=|a|):
Из свойства 10:
Тогда уравнение равносильно неравенству:
Метод











 Презентация на тему Формулы сокращенного умножения (Сумма и разность кубов)
Презентация на тему Формулы сокращенного умножения (Сумма и разность кубов)  График линейной функции с модулем
График линейной функции с модулем Вероятность, статистика и функциональная грамотность в итоговой и промежуточной аттестации по математике
Вероятность, статистика и функциональная грамотность в итоговой и промежуточной аттестации по математике Простейшие задачи. Теоретический тест в координатах. 9 класс
Простейшие задачи. Теоретический тест в координатах. 9 класс Проецирование многогранных и кривых поверхностей
Проецирование многогранных и кривых поверхностей Корень п-ой степени
Корень п-ой степени Комбинаторика и азартные игры
Комбинаторика и азартные игры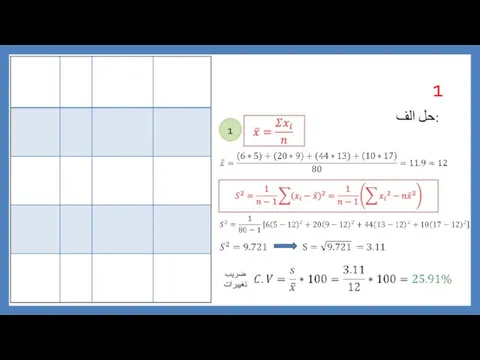 حل تمرین آمار
حل تمرین آمار Использование голосовых ассистентов на уроках математики в колледже
Использование голосовых ассистентов на уроках математики в колледже Ромб: признаки и свойства
Ромб: признаки и свойства Свойства степеней с натуральными показателями
Свойства степеней с натуральными показателями Сравнение чисел. Геометрические величины. Геометрические фигуры
Сравнение чисел. Геометрические величины. Геометрические фигуры Приёмы умножения числа 2
Приёмы умножения числа 2 Презентация на тему РАЦИОНАЛЬНЫЕ ЧИСЛА
Презентация на тему РАЦИОНАЛЬНЫЕ ЧИСЛА  Презентация на тему Геометрические тела и окружающий мир
Презентация на тему Геометрические тела и окружающий мир  Интегрирование неотрицательніх измериміх функций
Интегрирование неотрицательніх измериміх функций Разбор Мат.Вертикали. 6 класс
Разбор Мат.Вертикали. 6 класс Метод рационализации в логарифмических неравенствах
Метод рационализации в логарифмических неравенствах user_file_54317c3324dbe (1)
user_file_54317c3324dbe (1) Понятие десятичной дроби. Разряды десятичных дробей
Понятие десятичной дроби. Разряды десятичных дробей Кроссворд Площади фигур
Кроссворд Площади фигур Тест. Свойство простейших фигур
Тест. Свойство простейших фигур Описанная окружность
Описанная окружность Презентация на тему Логарифмическая функция, ее свойства и график
Презентация на тему Логарифмическая функция, ее свойства и график  Старинные меры длины
Старинные меры длины Задача сетевого планирования с вложением средств
Задача сетевого планирования с вложением средств Обобщающий урок по теме Многогранники
Обобщающий урок по теме Многогранники Повторение пройденного (1 класс)
Повторение пройденного (1 класс)