Содержание
- 2. Что же такое логика? Логика является одной из дисциплин, образующих математический фундамент информатики. В вычислительной технике
- 3. Этапы развития логики Первые учения о формах и способах рассуждений возникли в странах Древнего Востока (Китай,
- 4. В XVII веке немецкий ученый и философ Готфрид Вильгельм Лейбниц (1646 – 1716) попытался построить первые
- 5. Другой великий математик – англичанин Джордж Буль (1815 – 1864) открыл новую область науки – математическую
- 6. Основы логики В логике основным объектом является высказывание. Высказывание (суждение) - это форма мышления, с помощью
- 7. Определить что является высказыванием? Сканер - это устройство ввода. Прослушайте сообщение! 4+5=10 Кто отсутствует? Париж —
- 8. Определите истинность высказываний: Все медведи — бурые. Аристотель – основоположник логики. В прямоугольнике все углы прямые.
- 9. Высказывание называется простым, если никакая его часть сама не является высказыванием. Примеры: В каждом ромбе диагонали
- 10. Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами: А = {Аристотель - основоположник логики} В
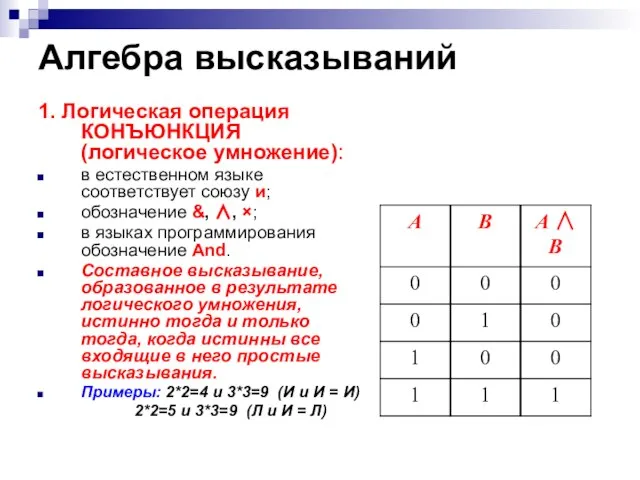
- 11. Алгебра высказываний 1. Логическая операция КОНЪЮНКЦИЯ (логическое умножение): в естественном языке соответствует союзу и; обозначение &,
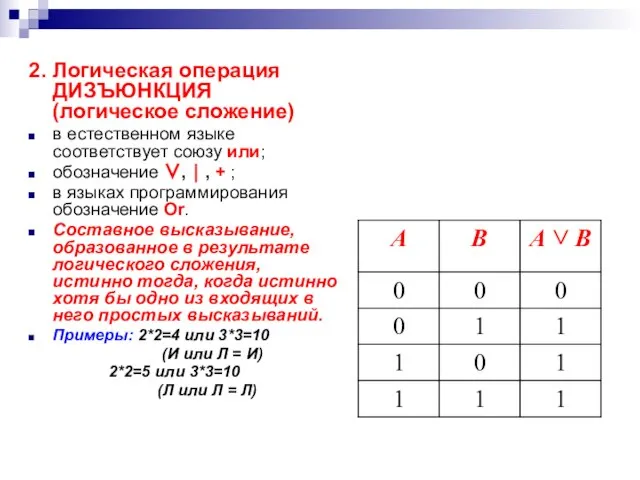
- 12. 2. Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение) в естественном языке соответствует союзу или; обозначение ∨, ⏐ ,
- 13. 3. Логическая операция ИНВЕРСИЯ (отрицание) в естественном языке соответствует словам неверно, что... и частице не; обозначение
- 14. 4.Логическая операция ИМПЛИКАЦИЯ (логическое следование): в естественном языке соответствует обороту если ..., то ...; обозначение ?
- 15. Примеры: Если число делится на 10, то оно делится на 5 – истинно, т.к. истинны и
- 16. 5.Логическая операция ЭКВИВАЛЕНТНОСТЬ (равнозначность): в естественном языке соответствует оборотам речи тогда и только тогда; в том
- 17. Примеры: А={Компьютер может вычислять} В={Компьютер включен} {Компьютер не может вычислять} ⇔ {Компьютер не включен} - истинно
- 18. Упражнения I. Выделите в составных высказываниях простые. Обозначьте каждое из них буквой; запишите с помощью логических
- 19. 2) Неверно, что Солнце движется вокруг Земли. (простое высказывание) В алгебре логики записывается = 1 (Истина)
- 20. 3) Сентябрь – осенний месяц или октябрь – зимний месяц. (составное высказывание) В алгебре логики записывается
- 21. Упражнения 3) Если сумма цифр числа 12 делится на 3, то число делится на 3 4)
- 22. II. Найдите значение выражения (5>6) &(3=4) (5 4) 0 0 0 & 0 = 0 1
- 23. III. Найдите значения логических выражений: а) (1 ∨ 0) ∨(1 ∨ 0); б) ((1 ∨ 0)
- 24. IV. Даны простые высказывания: А = {5>3}, В = {2=3} и С = {4 Определите истинность
- 25. Самостоятельно Даны простые высказывания: А = {Принтер – устройство ввода информации}, В = {Процессор – устройство
- 26. Решение: Даны простые высказывания: А = {Принтер – устройство ввода информации}, В = {Процессор – устройство
- 28. Скачать презентацию























 Комплексные числа и координатная плоскость. Решение примеров на построение комплексных чисел на комплексной плоскости
Комплексные числа и координатная плоскость. Решение примеров на построение комплексных чисел на комплексной плоскости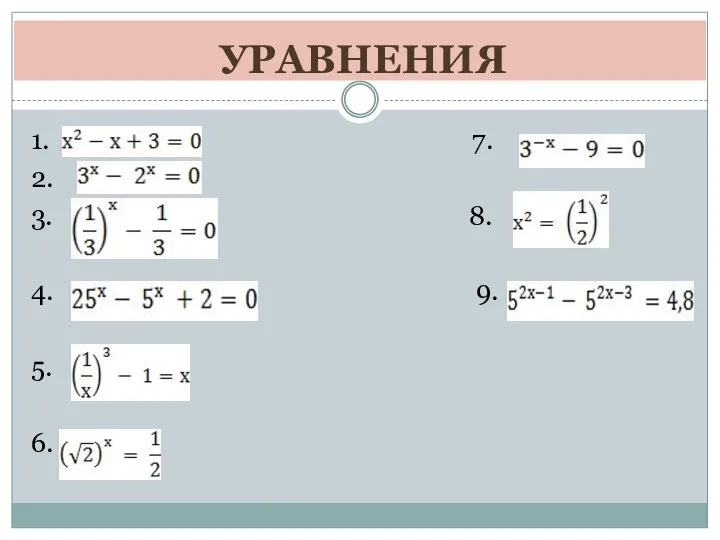 Решение показателей уравнений
Решение показателей уравнений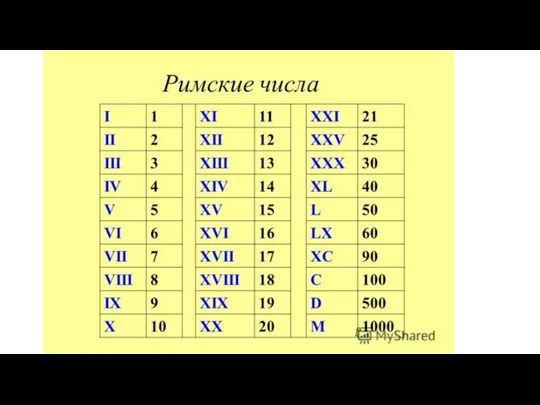 Римские числа
Римские числа Повторительно-обобщающий урок по теме: Показательная функция. 11 класс
Повторительно-обобщающий урок по теме: Показательная функция. 11 класс Теоремы о пределах. Нахождение пределов
Теоремы о пределах. Нахождение пределов Презентация на тему Средняя линия треугольника
Презентация на тему Средняя линия треугольника  Реши примеры устно. 2 класс
Реши примеры устно. 2 класс Декартова система координат
Декартова система координат Презентация на тему Математический КВН
Презентация на тему Математический КВН  Отображения (функции)
Отображения (функции) Диалектика как методология научного познания
Диалектика как методология научного познания Экологические понятия в математике
Экологические понятия в математике Треугольники. Геометрия, 7 класс
Треугольники. Геометрия, 7 класс ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА Параллельные прямые. 7 класс
Параллельные прямые. 7 класс Научные открытия России. Задача тысячелетия. Теорема Пуанкаре
Научные открытия России. Задача тысячелетия. Теорема Пуанкаре Дифференциальные уравнения и их применение в медицине
Дифференциальные уравнения и их применение в медицине Динамика системы вблизи цикла
Динамика системы вблизи цикла Деление с остатком
Деление с остатком Парная линейная регрессия
Парная линейная регрессия Компоненти дій
Компоненти дій Фигуры вращения
Фигуры вращения Элементы комбинаторики. Решение простейших комбинаторных задач
Элементы комбинаторики. Решение простейших комбинаторных задач Таблица умножения с 7 до 9
Таблица умножения с 7 до 9 Производная и первообразная
Производная и первообразная Какой многоугольник называется правильным? Приведите примеры правильных многоугольников
Какой многоугольник называется правильным? Приведите примеры правильных многоугольников Занимательные задачи
Занимательные задачи Основное свойство дроби
Основное свойство дроби