Подсчёт вероятности

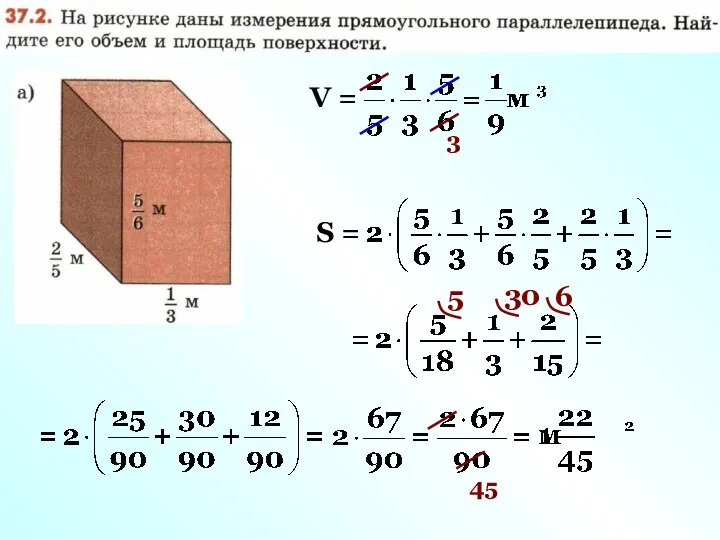
V =
3
S =
5
30
6
45

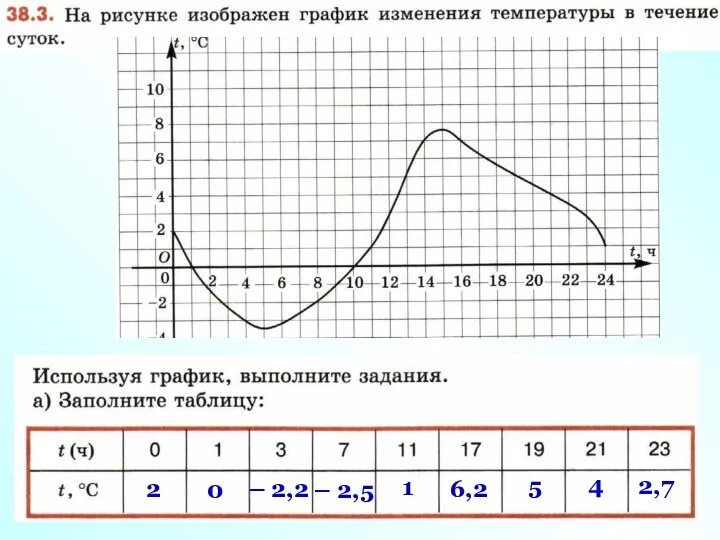
2
0
– 2,2
1
6,2
5
– 2,5
4
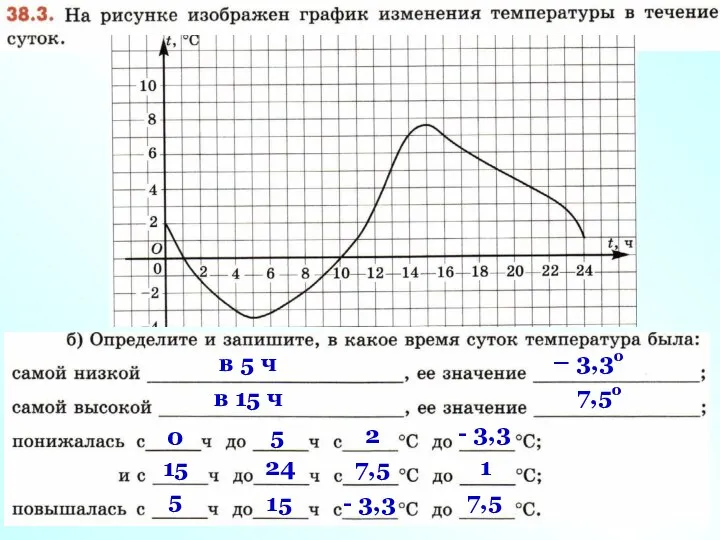
2,7

в 5 ч
– 3,3о
в 15 ч
7,5о
0
5
2
- 3,3
15
24
7,5
1
5
15
- 3,3
7,5

х + 7 = 3
– 4
х – 0,2 = – 3,4
– 3,2
х + 8 = – 12
– 20
х – 2,8 = 2,1
4,9
– 11 – х = 8
– 19
– 4,3 – х = 1,3
– 5,6
10 – х = – 4
14
– 0,45 – х = – 0,32
– 0,13

*
К л а с с н а я р а б о т а.

Семь букв разрезной азбуки : А, А, Б, Б, К, У, Ш – положены в мешок, откуда их вынимают наудачу и располагают одну за другой в том порядке, в котором они появляются. Может ли в результате получиться слово БАБУШКА?
А, А, Б, Б, К, У, Ш
1 2 3 4 5 6 7
4
7 ·
6 ·
5 ·
4 ·
3 ·
2 ·
1 =
5040
Р =
Р – вероятность (от фр. probabilite)

Задание. Подбросьте монету в 1 рубль 50 раз и подсчитайте, сколько раз выпадет «орёл».
В XVIII веке французский учёный, почётный член петербургской академии наук Бюффон для проверки правильности подсчёта вероятности выпадения «орла» подкинул монету 4040 раз. «Орёл» у него выпал 2048 раз.
Р =
0,506…
≈ 51%

В XIX веке английский учёный Пирсон подкинул монету 24000 раза. «Орёл» у него выпал 12012 раз.
Р =
0,5005
≈ 50%

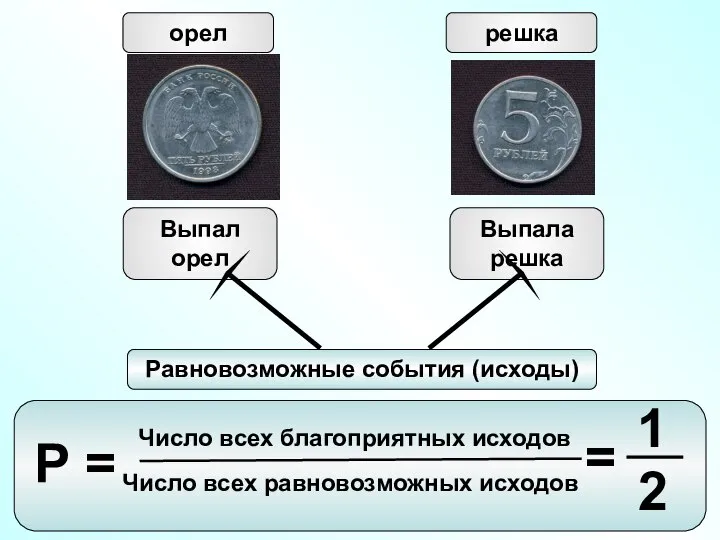
орел
решка
Выпал орел
Выпала решка
Число всех благоприятных исходов
Число всех равновозможных исходов
Р =
Равновозможные события (исходы)
=
1
2

Подсчёт вероятности
Достоверное событие – стопроцентная вероятность
100 % =
= 1
Невозможное событие – нулевая вероятность
0 % =
= 0

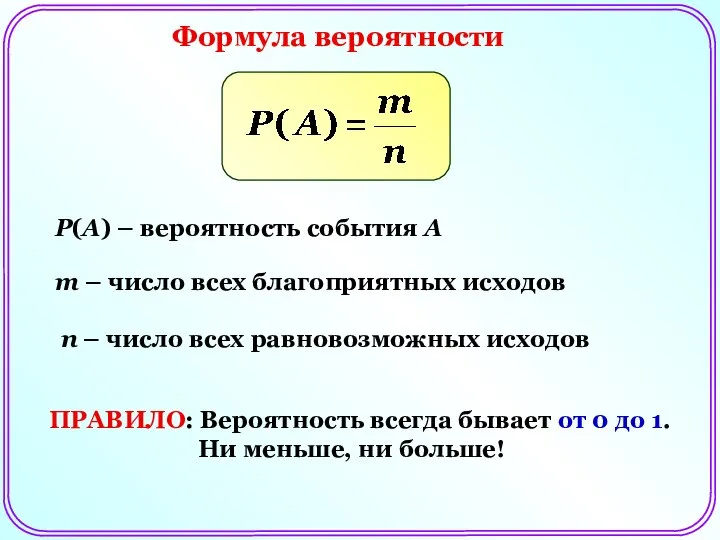
Формула вероятности
Р(А) – вероятность события А
m – число всех благоприятных исходов
n – число всех равновозможных исходов
ПРАВИЛО: Вероятность всегда бывает от 0 до 1. Ни меньше, ни больше!

Число граней:
Равновозможные исходы:
1, 2, 3, 4, 5, 6
6
1) Р =
2) Р =
3) Р =
4) Р =
5) Р =
6) Р =