Понятие многогранника. Правильные многогранники

Теория многогранников, в частности выпуклых многогранников,
— одна из самых увлекательных глав геометрии.
Л. А. Люстерник
С.Дали «Тайная вечеря»

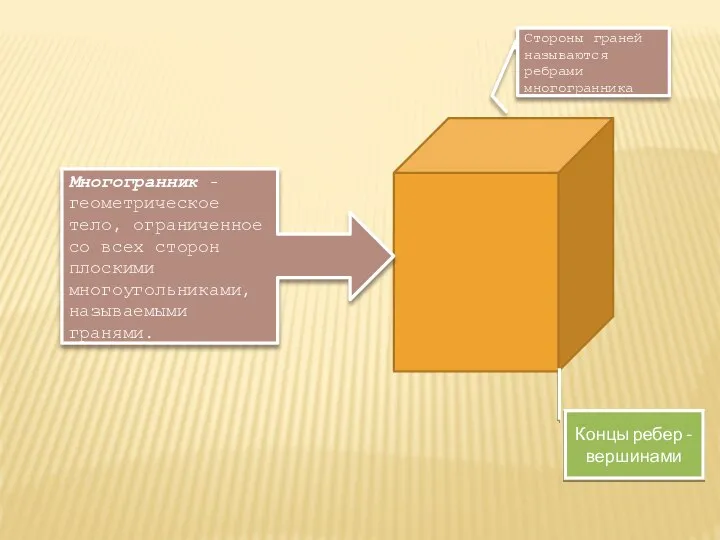
Стороны граней называются ребрами многогранника
Многогранник - геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями.
Концы ребер - вершинами

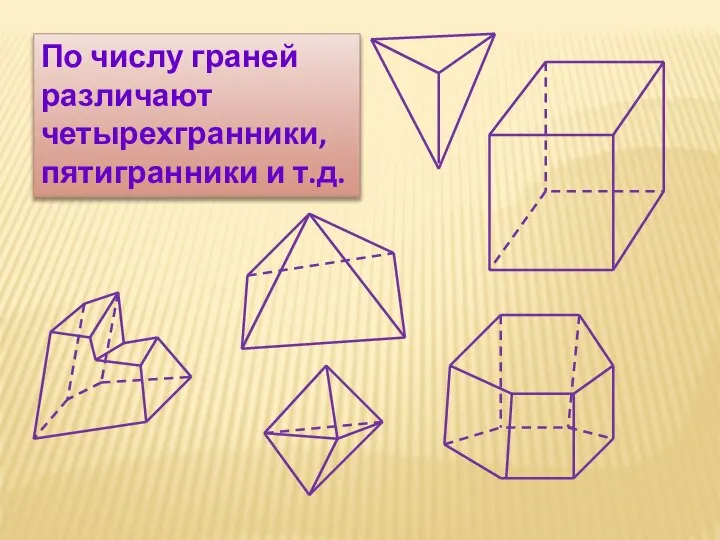
По числу граней различают четырехгранники, пятигранники и т.д.

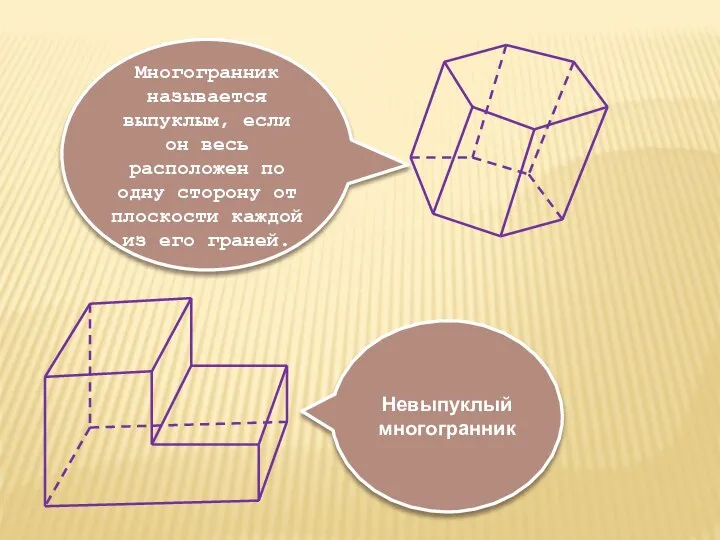
Невыпуклый многогранник
Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой из его граней.

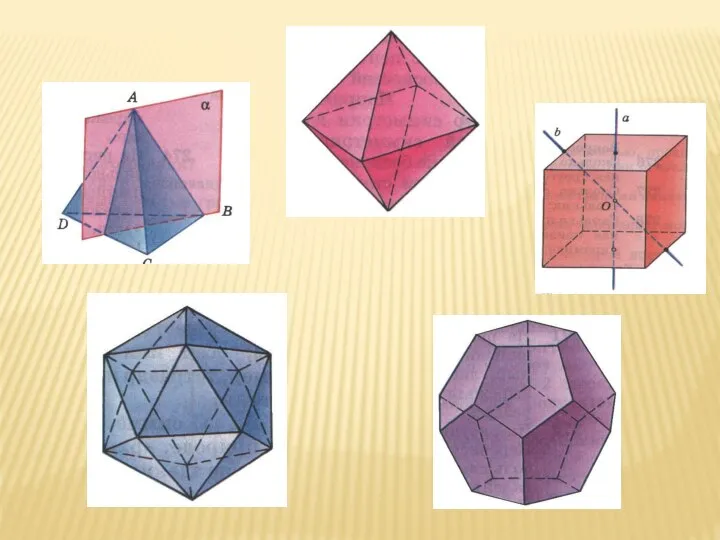
Правильные многогранники.
Многогранник называется правильным, если все его грани - равные между собой правильные многоугольники и в каждой его вершине сходится одно и то же число граней.
Известно только 5 выпуклых правильных многогранников.
Правильные выпуклые многогранники следующие: тетраэдр (4 грани); гексаэдр (6 граней) – это хорошо нам известный куб; октаэдр (8 граней); додекаэдр (12 граней); икосаэдр (20 граней).

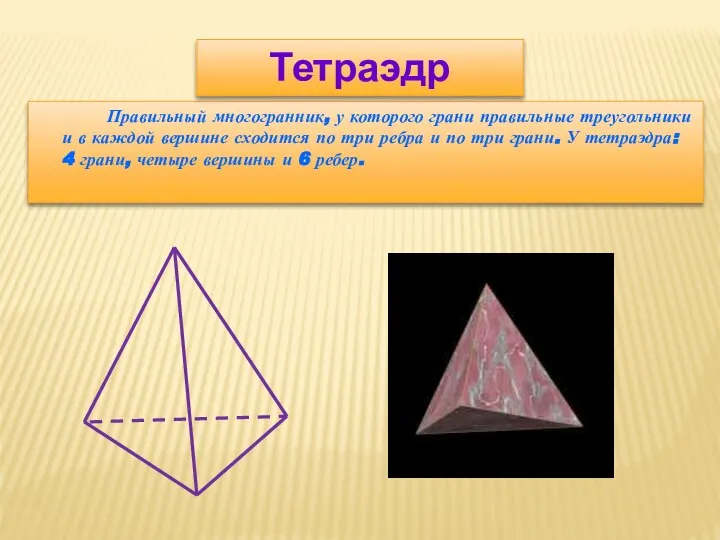
Правильный многогранник, у которого грани правильные треугольники и в каждой вершине сходится по три ребра и по три грани. У тетраэдра: 4 грани, четыре вершины и 6 ребер.
Тетраэдр

Правильный многогранник, у которого грани- правильные треугольники и в каждой вершине сходится по четыре ребра и по четыре грани. У октаэдра: 8 граней, 6 вершин и 12 ребер
Октаэдр

Правильный многогранник, у которого грани – квадраты и в каждой вершине сходится по три ребра и три грани. У него: 6 граней, 8 вершин и 12 ребер.
Куб

Додекаэдр
Правильный многогранник, у которого грани правильные пятиугольники и в каждой вершине сходится по три ребра и три грани. У додекаэдра:12 граней, 20 вершин и 30 ребер.

Икосаэдр
Правильный многогранник, у которого грани правильные треугольники и в каждой вершине сходится по пять ребер и пять граней. У икосаэдра: 20 граней, 12 вершин и 30 ребер.

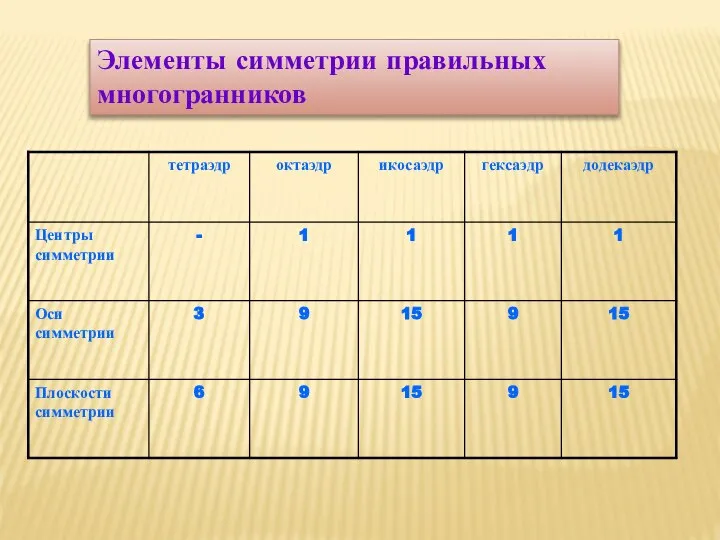
Элементы симметрии правильных многогранников

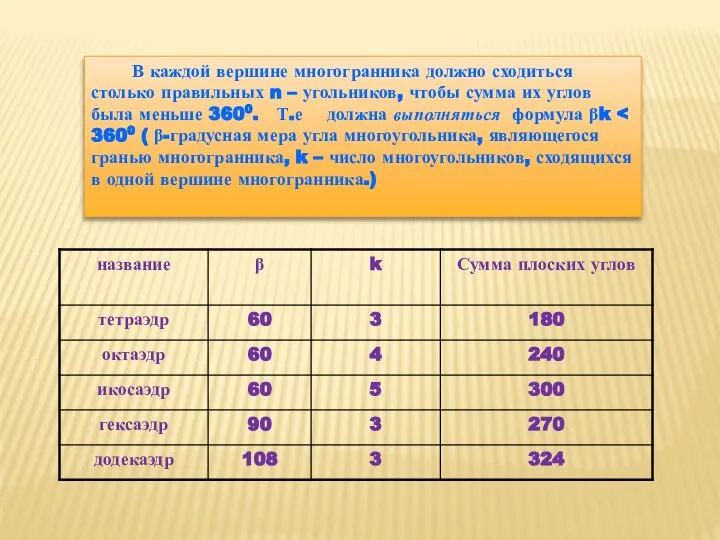
В каждой вершине многогранника должно сходиться столько правильных n – угольников, чтобы сумма их углов была меньше 3600. Т.е должна выполняться формула βk < 3600 ( β-градусная мера угла многоугольника, являющегося гранью многогранника, k – число многоугольников, сходящихся в одной вершине многогранника.)

Теорема Эйлера:
Число вершин - число ребер + число граней =2
Один из величайших математиков мира, работы которого оказали решающее влияние на развитие многих современных разделов математики.
Л.Эйлер
(1707-1783)

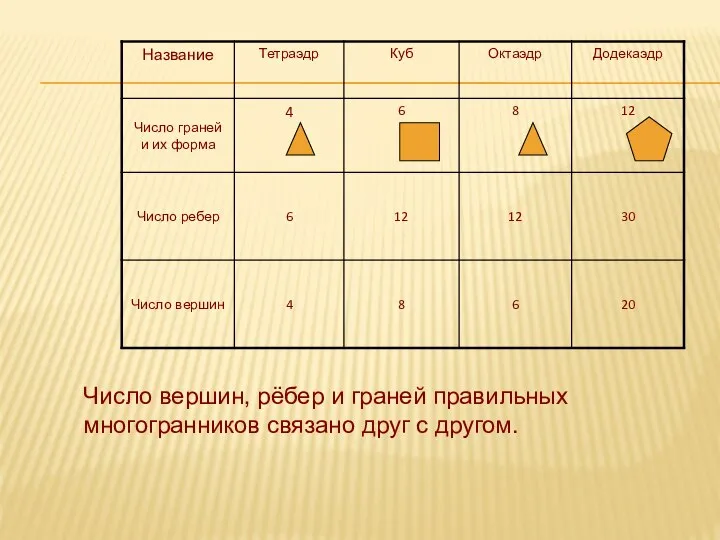
Число вершин, рёбер и граней правильных многогранников связано друг с другом.

Все типы правильных многогранников были известны в Древней Греции – именно им посвящена завершающая, XIII книга «Начал» Евклида.
Немного истории

Правильные многогранники называют также «платоновыми телами» - они занимали видное место в идеалистической картине мира древнегреческого философа Платона.
Додекаэдр символизировал всё мироздание, почитался главнейшим. Уже по латыни в средние века его стали называть «пятая сущность» или guinta essentia, «квинта эссенциа», отсюда происходит вполне современное слово «квинтэссенция», означающее всё самое главное, основное, истинную сущность чего-либо.

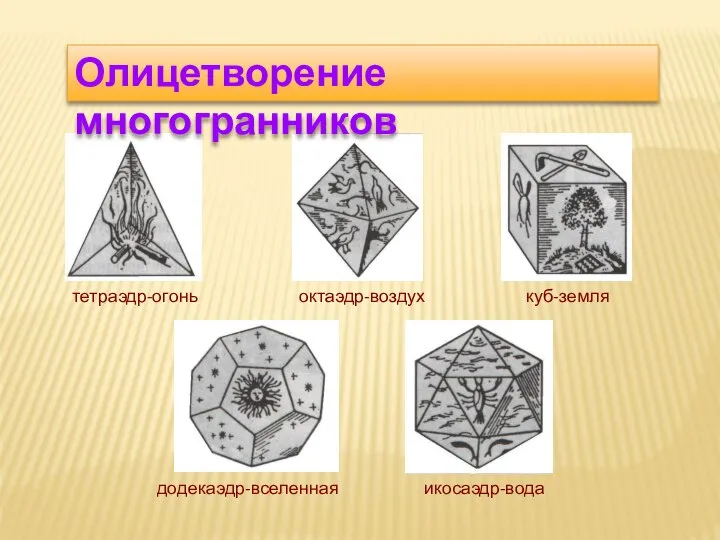
Олицетворение многогранников
додекаэдр-вселенная
икосаэдр-вода
октаэдр-воздух
куб-земля
тетраэдр-огонь

Звездчатые правильные многогранники

.
Существует семейство тел, родственных платоновым - это полуправильные выпуклые многогранники, или Архимедовы тела. У них все многогранные углы равны, все грани - правильные многоугольники, но нескольких различных типов.

«Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая мою геометрию»

Кристаллы — тела, имеющие многогранную форму. Вот один из примеров таких тел: кристалл пирита (сернистый колчедан FeS) — природная модель додекаэдра. Пирит (от греч. “пир” — огонь) — сернистое железо или серный колчедан, наиболее распространенный минерал из группы сульфидов. Размеры кристаллов пирита часто достигают нескольких сантиметров и являются хорошим коллекционным материалом. От других подобных ему минералов отличается твердостью: царапает стекло.

Создания природы красивы и симметричны. В кристаллографии существует раздел, который называется «геометрическая кристаллография»

ЕСЛИ НАБЛЮДАТЬ И РАССМАТРИВАТЬ МНОГОГРАННЫЕ ФОРМЫ, ТО МОЖНО НЕ ТОЛЬКО ПОЧУВСТВОВАТЬ ИХ КРАСОТУ, НО И ОБНАРУЖИТЬ НЕКОТОРЫЕ ЗАКОНОМЕРНОСТИ, ВОЗМОЖНО, ИМЕЮЩИЕ ПРИКЛАДНОЕ ЗНАЧЕНИЕ.
Некоторые из правильных и полуправильных тел встречаются в природе
в виде кристаллов,
другие — в виде
вирусов, простейших
микроорганизмов.
Вирусы

В эпоху Возрождения большой интерес к формам правильных многогранников проявили скульпторы. Знаменитый художник, увлекавшийся геометрией Альбрехт Дюрер (1471- 1528) , в известной гравюре ''Меланхолия '‘ на переднем плане изобразил додекаэдр.

Многогранники в архитектуре.
Великая пирамида в Гизе
Александрийский маяк

Замечено, что наша матушка-Земля последовательно проходит эволюцию правильных объемных фигур. Существует много данных о сравнении структур и процессов Земли с вышеуказанными фигурами. Полагают, что четырем геологическим эрам Земли соответствуют четыре силовых каркаса правильных Платоновских тел:
Протозою - тетраэдр (четыре плиты),
Палеозою - гексаэдр (шесть плит),
Мезозою - октаэдр (восемь плит),
Кайнозою - додекаэдр (двенадцать плит).

Гипотеза В.Макарова и В.Морозова:
Ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете.
Лучи кристалла обуславливают икосаэдро-додекаэрическую структуру Земли, проявляющуюся в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. 62 их вершины и середины ребер, называемые узлами, оказывается, обладают рядом специфичecких свойств, позволяющих объяснить многие непонятные явления.

Если нанести на глобус очаги наиболее крупных и примечательных культур и цивилизаций Древнего мира, можно заметить закономерность в их расположении относительно географических полюсов и экватора планеты. Многие залежи полезных ископаемых тянутся вдоль икосаэдрово-додекаэдровой сетки. Еще более удивительные вещи происходят в местах пересечения этих ребер: тут располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана, здесь шотландское озеро Лох-Несс, Бермудский треугольник. Дальнейшие исследования Земли, возможно, определят отношение к этой красивой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место.

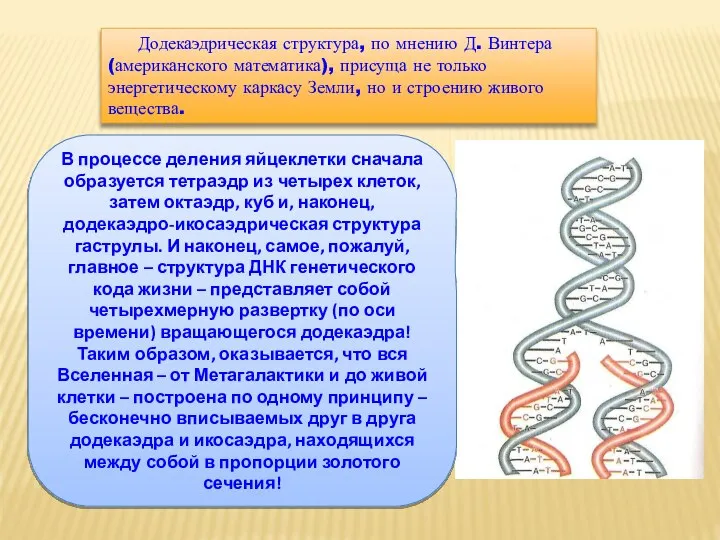
Додекаэдрическая структура, по мнению Д. Винтера (американского математика), присуща не только энергетическому каркасу Земли, но и строению живого вещества.
В процессе деления яйцеклетки сначала образуется тетраэдр из четырех клеток, затем октаэдр, куб и, наконец, додекаэдро-икосаэдрическая структура гаструлы. И наконец, самое, пожалуй, главное – структура ДНК генетического кода жизни – представляет собой четырехмерную развертку (по оси времени) вращающегося додекаэдра! Таким образом, оказывается, что вся Вселенная – от Метагалактики и до живой клетки – построена по одному принципу – бесконечно вписываемых друг в друга додекаэдра и икосаэдра, находящихся между собой в пропорции золотого сечения!

Впрочем, многогранники - отнюдь не только объект научных исследований. Их формы - завершенные и причудливые, широко используются в декоративном искусстве.

Титульный лист книги
Ж. Кузена «Книга о перспективе»

Ярчайшим примером художественного изображения многогранников в XX веке являются, конечно, графические фантазии Маурица Корнилиса Эшера (1898-1972), голландского художника, родившегося в Леувардене.
Мауриц Эшер в своих рисунках как бы открыл и интуитивно проиллюстрировал законы сочетания элементов симметрии, т.е. те законы, которые властвуют над кристаллами, определяя и их внешнюю форму, и их атомную структуру, и их физические свойства.
Математик, так же как и художник или поэт, создает узоры, и если его узоры более устойчивы, то лишь потому, что они составлены из идей.