Презентация на тему Золотое сечение-гармония математики

Содержание:
Вступление
История «Золотого сечения»
Математическое понимание гармонии
Понятие «Золотое сечение»
«Золотое сечение» - гармония математики
Золотое сечение в геометрии
Вывод

Вступление
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались многие ученые. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
Что же такое «золотое сечение»?

История «Золотого сечения»
В Древнем Египте существовала «система правил гармонии», основанная на Золотом Сечении.
В Древней Греции Золотое Сечение было своеобразным каноном культуры, который пронизывает все сферы науки и искусства. Красота и гармония стали важнейшими категориями познания.
В толковании древних греков понятие золотого сечения, и понятие гармонии идентичны.
Согласно Пифагору гармония имеет численное выражение, то есть, она связана с концепцией числа.
Евклид излагает теорию Платоновых тел, которая является существенным разделом геометрической теории Золотого Сечения.
Теория гармонии Древних

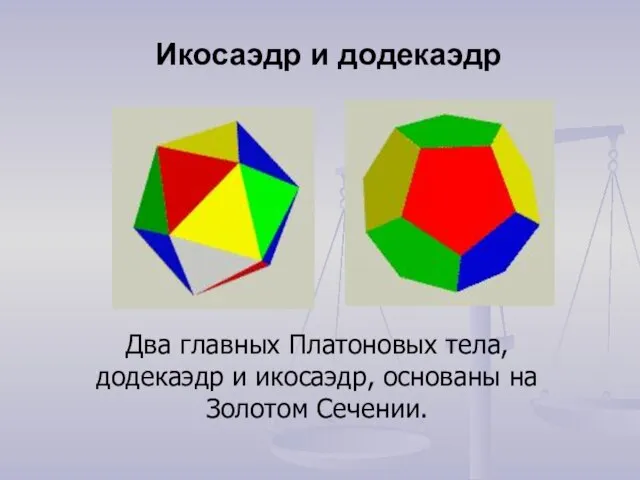
Два главных Платоновых тела, додекаэдр и икосаэдр, основаны на Золотом Сечении.
Икосаэдр и додекаэдр

Ряд Фибоначчи
С историей золотого сечения связано имя итальянского математика Леонардо Фибоначчи.
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи.
Каждый член последовательности, начиная с третьего, равен сумме двух предыдущих, а отношение смежных чисел ряда приближается к отношению золотого деления.
Все исследователи золотого деления в растительном и в животном мире, искусстве, неизменно приходили к ряду Фибоначчи как арифметическому выражению закона золотого деления.

«Золотая Пропорция» - главный эстетический принцип эпохи Средневековья
Эпоха Возрождения ассоциируется с именами таких «титанов», как Леонардо да Винчи, Микеланджело, Рафаэль, Николай Коперник, Альберт Дюрер, Лука Пачоли.
Имеется много авторитетных свидетельств о том, что именно Леонардо да Винчи(1452-1519) был одним из первых, кто ввел сам термин «Золотое Сечение».
Доказано, что во многих своих произведениях Леонардо да Винчи использовал пропорции золотого сечения, в частности, в своей всемирно известной фреске «Тайная вечеря» и непревзойденной «Джоконде.

«Витрувийский человек»
Леонардо да Винчи
Разрабатывая правила изображения человеческой фигуры, Леонардо да Винчи пытался на основе литературных сведений древности восстановить так называемый «квадрат древних».
Он выполнил рисунок, в котором показано, что размах вытянутых в сторону рук человека примерно равен его росту, вследствие чего фигура человека вписывается в квадрат и в круг.
При исследовании рисунка можно заметить, что комбинация рук и ног в действительности составляет четыре различных позы.
Рисунок и текст иногда называют каноническими пропорциями.

Вклад Кеплера
в теорию Золотого Сечения
Гениальный астроном Иоганн Кеплер (1571-1630) был последовательным приверженцем Золотого Сечения, Платоновых тел и Пифагорейской доктрины о числовой гармонии Мироздания.
Считается, что именно Кеплер обратил внимание на ботаническую закономерность филлотаксиса и установил связь между числами Фибоначчи и золотой пропорцией, доказав, что последовательность отношений соседних чисел Фибоначчи:
1/1; 2/1; 3/2; 5/3 ;8/5; 13/8;…в пределе стремится к золотой пропорции

Математическое понимание гармонии
«Гармония – соразмерность частей и целого, слияние различных компонентов объекта в единое органическое целое. В гармонии получают внешнее выявление внутренняя упорядоченность и мера бытия» -Большая Советская Энциклопедия
Математическая гармония - это равенство или соразмерность частей с друг другом и части с целым.
Понятие математической гармонии тесно связано с понятиями пропорции и симметрии.

Понятие «Золотое сечение»
a : b = b : c или с : b = b : а
Золотое сечение - деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.

Эта пропорция равна:
Золотое сечение в процентах

Число j является положительным корнем квадратного уравнения:
x2 = x + 1
подставим корень j вместо x и разделим на j :
Если продолжить такую подстановку бесконечное число раз, то получим цепную дробь:
Аналогично, если взять корень квадратный из правой и левой частей тождества (1) то получим представление золотой пропорции в «радикалах»:
(2)
(3)
(1)
(4)
Эти формулы (3) и (4) доставляют «эстетическое наслаждение» и вызывают неосознанное чувство ритма и гармонии…
«Золотое сечение» - гармония математики

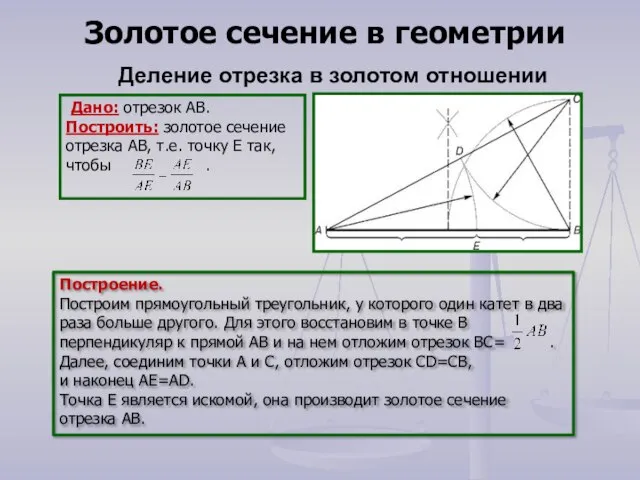
Дано: отрезок АВ.
Построить: золотое сечение отрезка АВ, т.е. точку Е так, чтобы .
Построение.
Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок ВС= .
Далее, соединим точки А и С, отложим отрезок CD=CB,
и наконец AE=AD.
Точка Е является искомой, она производит золотое сечение отрезка АВ.
Деление отрезка в золотом отношении
Золотое сечение в геометрии

А
В
С
Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся в золотом отношении:
Золотой треугольник

Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение длины к ширине даёт число φ, называется золотым прямоугольником.
Золотой прямоугольник

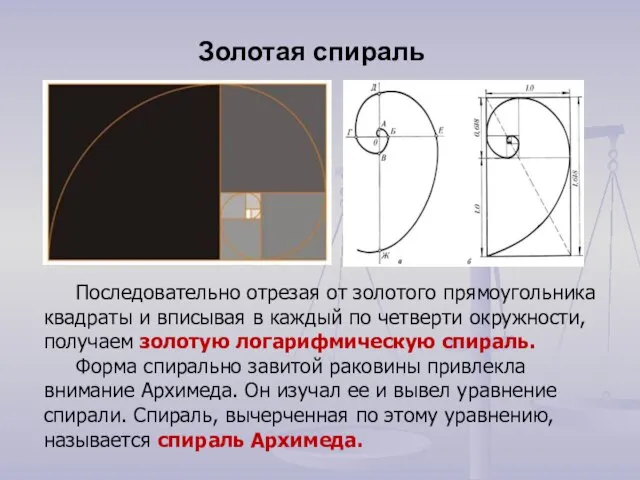
Последовательно отрезая от золотого прямоугольника квадраты и вписывая в каждый по четверти окружности, получаем золотую логарифмическую спираль.
Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется спираль Архимеда.
Золотая спираль

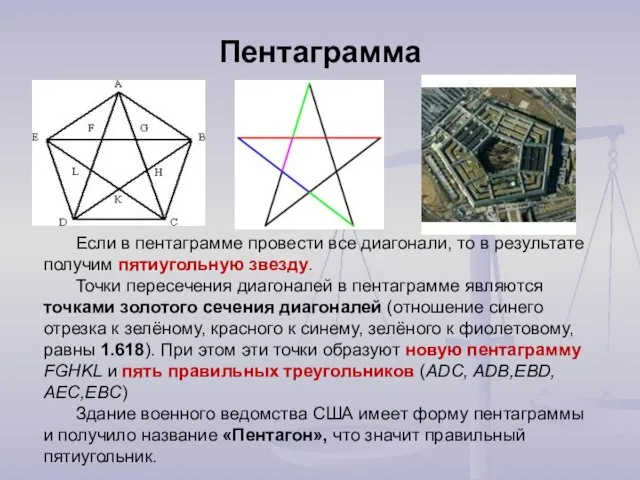
Пентаграмма
Если в пентаграмме провести все диагонали, то в результате получим пятиугольную звезду.
Точки пересечения диагоналей в пентаграмме являются точками золотого сечения диагоналей (отношение синего отрезка к зелёному, красного к синему, зелёного к фиолетовому, равны 1.618). При этом эти точки образуют новую пентаграмму FGHKL и пять правильных треугольников (ADC, ADB,EBD, AEC,EBC)
Здание военного ведомства США имеет форму пентаграммы и получило название «Пентагон», что значит правильный пятиугольник.