Слайд 9ЕГЭ-2019
4. Первый сплав содержит 5 % меди, второй — 14 % меди. Масса

второго сплава больше массы первого сплава на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 10 % меди. Найдите массу третьего сплава.
Решение. Пусть масса первого сплава x кг, второго (x + 7) кг, третьего — (2x + 7) кг. Меди было в первом сплаве 0,05x кг, во втором — 0,14(x + 7) кг, в третьем — 0,1(2x + 7) кг. Составим уравнение:
0,05x + 0,14(x + 7) = 0,1(2x + 7).
Слайд 11ЕГЭ-2017
5. Смешав 70 %-й и 60 %-й растворы кислоты и добавив 2 кг

чистой воды, получили 50 %-й раствор кислоты. Если бы вместо 2 кг воды добавили 2 кг 90 %-го раствора той же кислоты, то получили бы 70 %-й раствор кислоты. Сколько килограммов 70 %-го раствора кислоты использовали для получения смеси?
Решение. Пусть масса первого сплава x кг, второго (x + 7) кг, третьего — (2x + 7) кг. Найдём массу меди в каждом из трёх сплавов. Меди было в первом сплаве 0,05x кг, во втором — 0,14(x + 7) кг, в третьем — 0,1(2x + 7) кг. Составим уравнение: 0,05x + 0,14(x + 7) = 0,1(2x + 7).
Слайд 17Задачи для самостоятельного решения
7. Имеется 400 г морской воды, содержащей 4 %

соли. Сколько граммов чистой воды нужно добавить в эту морскую воду, чтобы новый раствор содержал 2 % соли?
8. (2016) В сосуд, содержащий 10 литров 24-процентного водного раствора некоторого вещества, добавили 5 литров воды. Определите процентную концентрацию того же вещества в новом растворе.
9. (2009) В бидон налили 4 литра молока трёхпроцентной жирности и 6 литров молока шестипроцентной жирности. Сколько процентов составляет жирность молока в бидоне?.
















 Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов
Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов Решение задач. 1 класс
Решение задач. 1 класс Рациональные уравнения
Рациональные уравнения Признаки параллельности прямых
Признаки параллельности прямых Интегрированный урок в 7 классе Грамотная геометрия - геометрия + русский язык
Интегрированный урок в 7 классе Грамотная геометрия - геометрия + русский язык Интегрированный урок алгебры и экономики. 7 класс
Интегрированный урок алгебры и экономики. 7 класс Веселые примеры
Веселые примеры Использование логических операций в теории множеств. Инверсия
Использование логических операций в теории множеств. Инверсия Автор: Стребкова Виктория Ученица 5 класса
Автор: Стребкова Виктория Ученица 5 класса Многочлены над числовыми полями
Многочлены над числовыми полями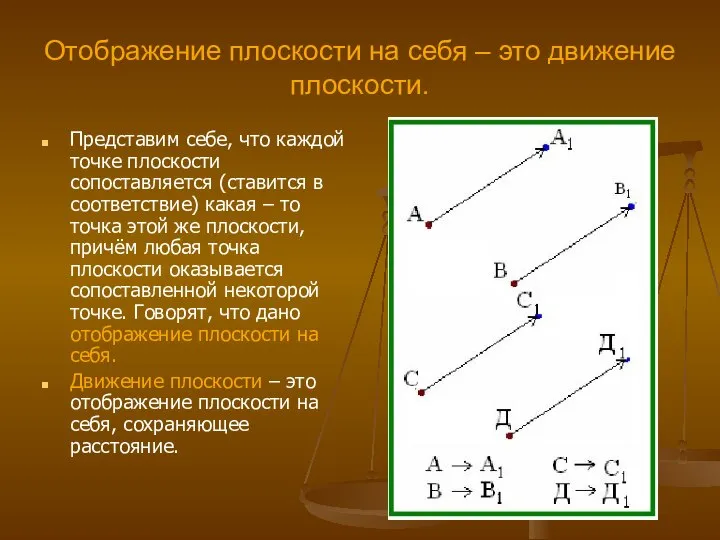 Геометрические преобразования плоскости
Геометрические преобразования плоскости Урок математики в 1 классе
Урок математики в 1 классе Приемы вычитания с переходом через разряд вида 35 - 7
Приемы вычитания с переходом через разряд вида 35 - 7 Числовые выражения
Числовые выражения Множество. Элемент множества
Множество. Элемент множества Литература
Литература Стереометрия. Многогранники
Стереометрия. Многогранники Приёмы умножения числа 2
Приёмы умножения числа 2 Невозможный треугольник
Невозможный треугольник Презентация на тему Умножение и деление чисел на 2 и на 3 (2 класс)
Презентация на тему Умножение и деление чисел на 2 и на 3 (2 класс)  Этапы моделирования
Этапы моделирования Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Обыкновенные дроби
Обыкновенные дроби Задачи и примеры. 1 класс
Задачи и примеры. 1 класс Понятия длиннее, короче, одинаковые по длине
Понятия длиннее, короче, одинаковые по длине Тест Смешанные числа
Тест Смешанные числа Усный счет
Усный счет Презентация на тему Буквенные выражения (2 класс)
Презентация на тему Буквенные выражения (2 класс)