Содержание
- 2. Свойства графов, которые мы будем изучать в данной главе, присущи графам общего вида и не зависят
- 3. 4.1. Цикломатическое число
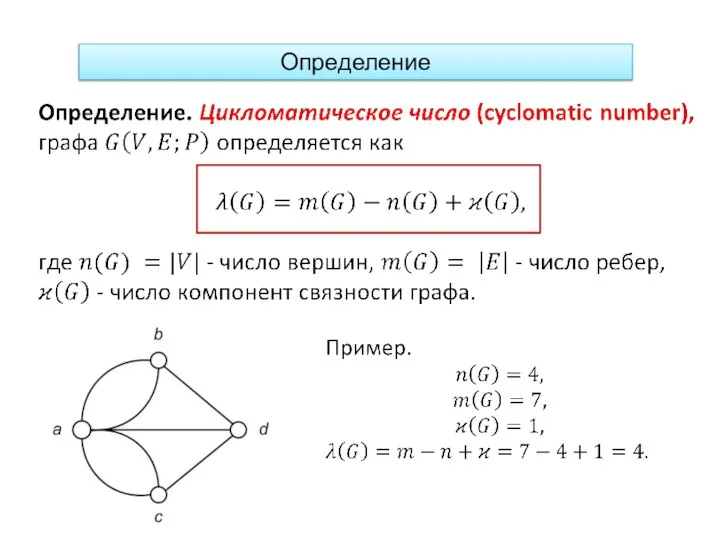
- 4. Определение
- 5. Цикловые ребра и перешейки Назовем ребро цикловым, если оно содержится хотя бы в одном цикле; в
- 7. Свойства цикломатического числа
- 9. 4.2. Деревья
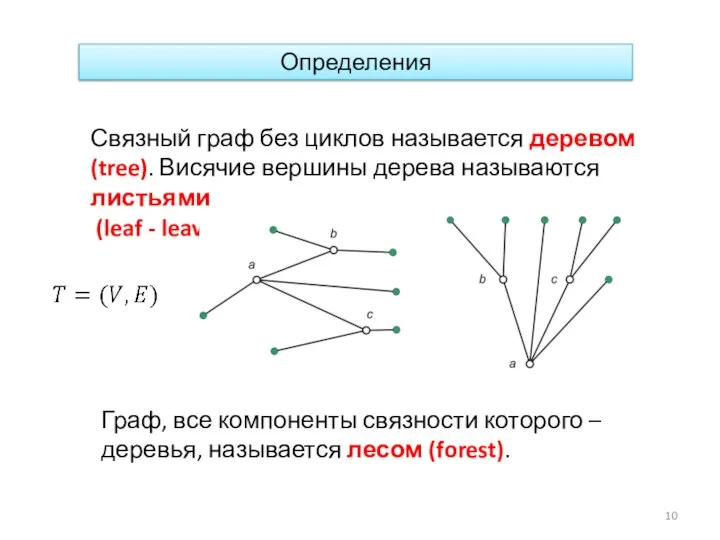
- 10. Определения Связный граф без циклов называется деревом (tree). Висячие вершины дерева называются листьями (leaf - leaves).
- 11. Свойства дерева
- 13. Свойство 5. Добавление ребра (разумеется, без добавления вершины) приводит к увеличению λ на единицу, то есть
- 14. 4.3. Каркасы
- 15. Определение Каркас связного графа является деревом.
- 16. Алгоритм нахождения каркаса Алгоритм является модификацией волнового алгоритма нахождения кратчайшей цепи. Шаг 1. Выберем произвольную вершину
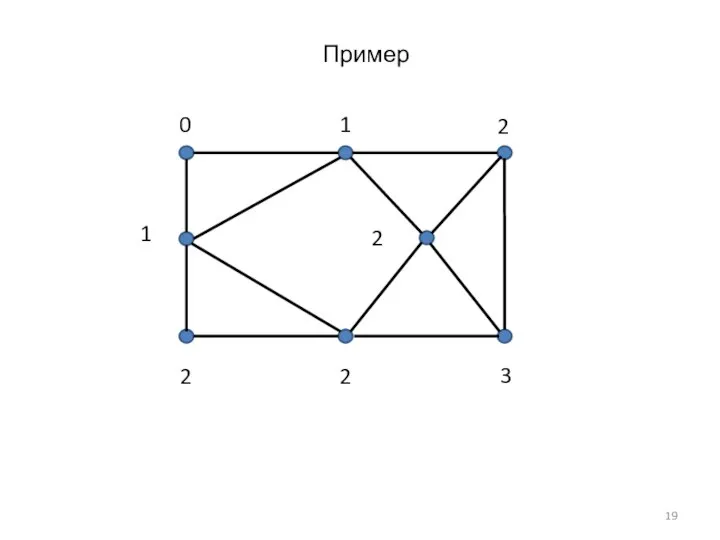
- 19. Пример 0 1 1 2 2 2 2 3
- 20. Кратчайший каркас графа
- 21. Алгоритм Прима
- 22. Robert C. Prim (b. 1921) along with coworker Joseph Kruskal developed two different algorithms (see greedy
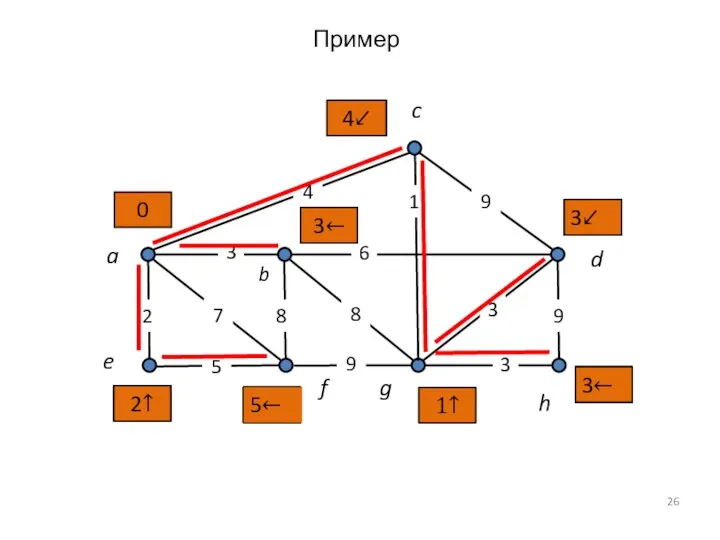
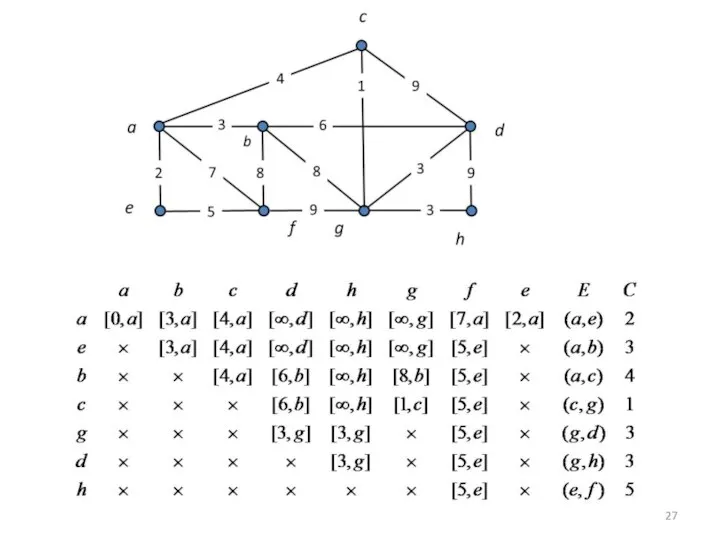
- 26. f a b c d e g h 4 3 2 7 8 6 8 1
- 28. Теорема о хорде каркаса
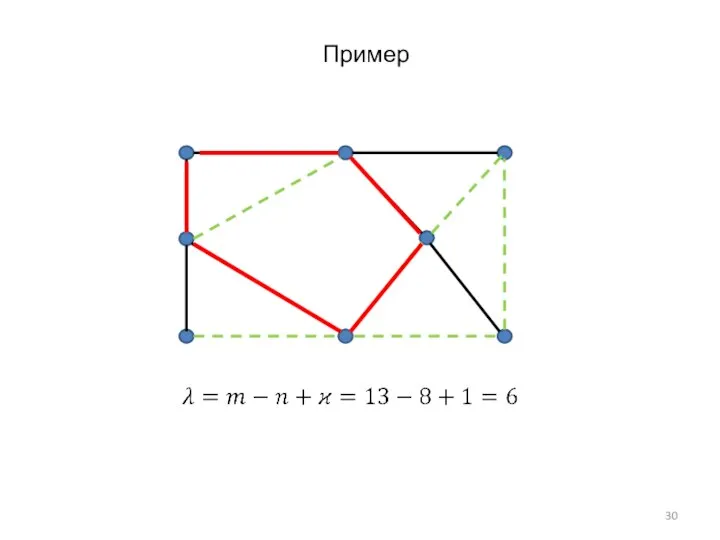
- 30. Пример
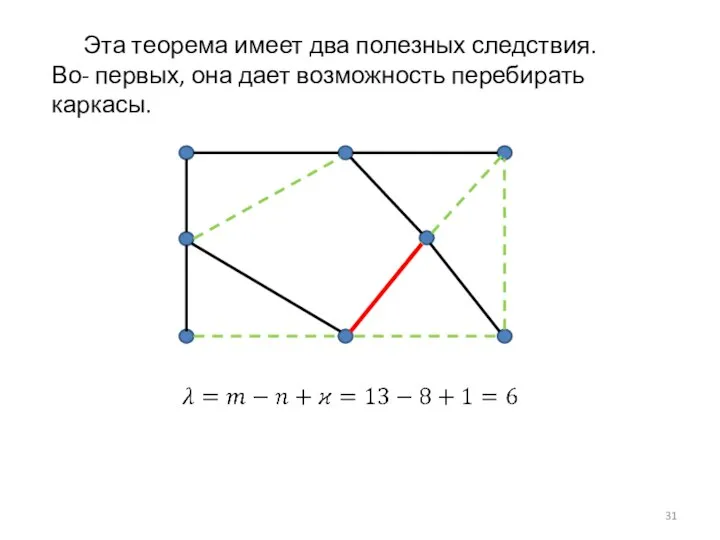
- 31. Эта теорема имеет два полезных следствия. Во- первых, она дает возможность перебирать каркасы.
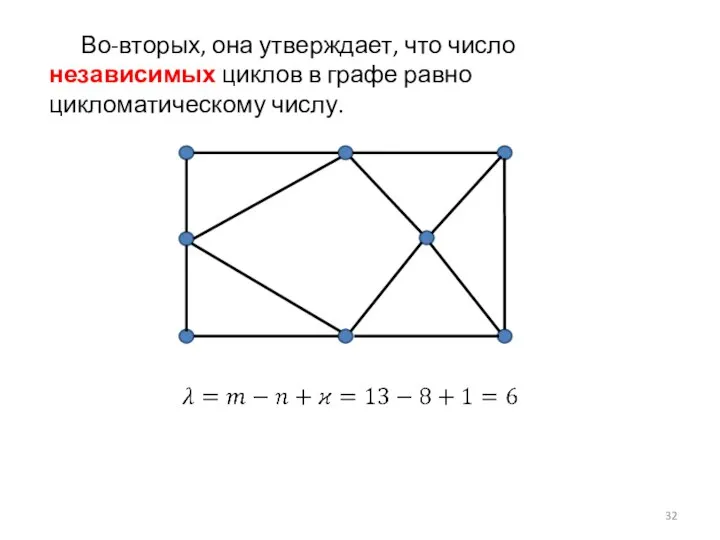
- 32. Во-вторых, она утверждает, что число независимых циклов в графе равно цикломатическому числу.
- 33. Каждому суграфу G ’=(V,E ’) графа G=(V,E) взаимно однозначно соответствует подмножество ребер E ’⊆E ; каждое
- 34. Однореберные суграфы линейно независимы, а любой суграф есть их линейная комбинация = Пример: сумма суграфов (1,1,0,1)
- 35. В этом разделе цикл определяется как суграф, все вершины ко- торого имеют четные валентности. Сумма двух
- 37. Скачать презентацию


























 Пперпендикулярные прямые
Пперпендикулярные прямые Решение текстовых задач с помощью уравнений
Решение текстовых задач с помощью уравнений Логические операции
Логические операции Задачи на кратное сравнение
Задачи на кратное сравнение Связь суммы со слагаемыми
Связь суммы со слагаемыми Решение задач с помощью систем уравнений (часть 2)
Решение задач с помощью систем уравнений (часть 2) Сечение куба, призмы, пирамиды
Сечение куба, призмы, пирамиды Основные понятия и определения метрологии. Лекция 1
Основные понятия и определения метрологии. Лекция 1 Математическая викторина. 2 тур. Великие и знаменитые
Математическая викторина. 2 тур. Великие и знаменитые Сократите дробь решите систему, уравнение, упростите выражение и т.д
Сократите дробь решите систему, уравнение, упростите выражение и т.д Показательная функция и ее применение
Показательная функция и ее применение Таблицы. Алгебра 7 класс
Таблицы. Алгебра 7 класс Расстояние от точки до прямой. Решение задач
Расстояние от точки до прямой. Решение задач Перпендикуляр и наклонная
Перпендикуляр и наклонная Математическое моделирование
Математическое моделирование Арифметическая прогрессия. Всё в твоих руках
Арифметическая прогрессия. Всё в твоих руках ПРОЕКТ: Реализация требований ФГОС ООО при обучении учащихся 6 класса теме «Сложение и вычитание рациональных чисел»
ПРОЕКТ: Реализация требований ФГОС ООО при обучении учащихся 6 класса теме «Сложение и вычитание рациональных чисел» 3_Equations_2
3_Equations_2 Выражения с переменными
Выражения с переменными Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Методика изучения геометрического материала
Методика изучения геометрического материала Соотношение числа и цифры. Считаем от 1 до 9
Соотношение числа и цифры. Считаем от 1 до 9 Задачи на нахождение неизвестного по двум разностям
Задачи на нахождение неизвестного по двум разностям Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1
Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1 Формулы тангенсов и котангенсов
Формулы тангенсов и котангенсов Уравнение древности. Франсуа Виет
Уравнение древности. Франсуа Виет Великолепная пятерка. Математический калейдоскоп
Великолепная пятерка. Математический калейдоскоп Умножение обыкновенных дробей
Умножение обыкновенных дробей