Ур3

Цели обучения:
10.2.1 - знать аксиомы стереометрии, их следствия; иллюстрировать и записывать их с помощью математических символов;

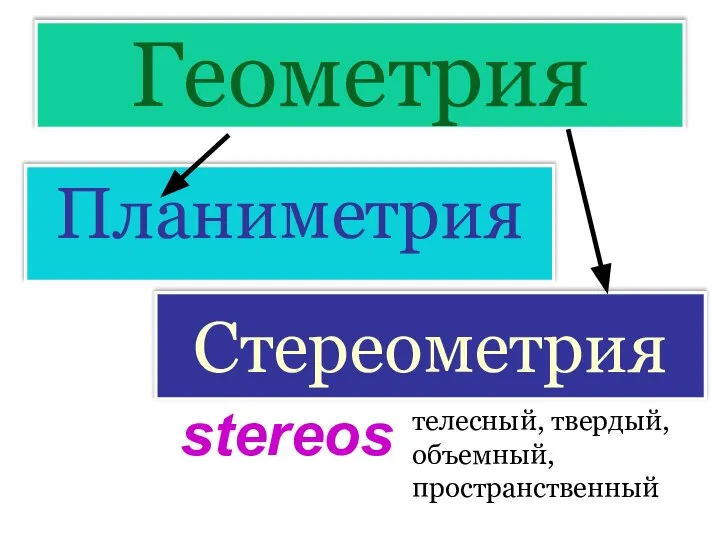
Геометрия
Планиметрия
Стереометрия
stereos
телесный, твердый, объемный, пространственный

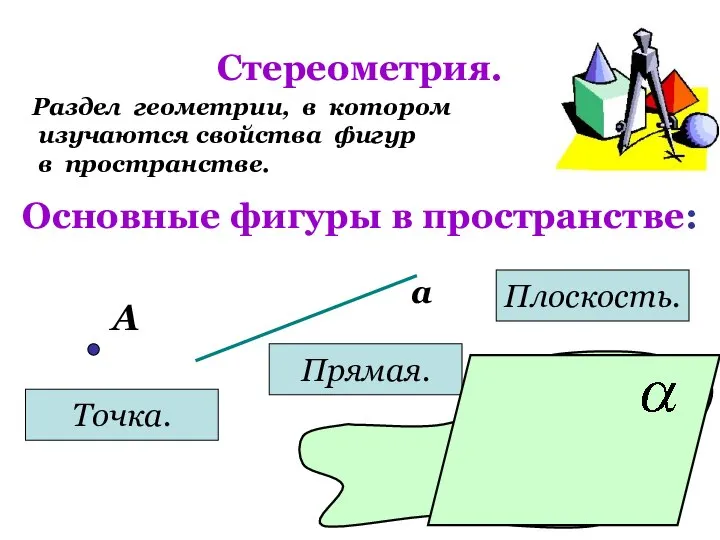
Стереометрия.
Раздел геометрии, в котором
изучаются свойства фигур
в пространстве.
Основные фигуры в пространстве:
А
Точка.
а
Прямая.
Плоскость.

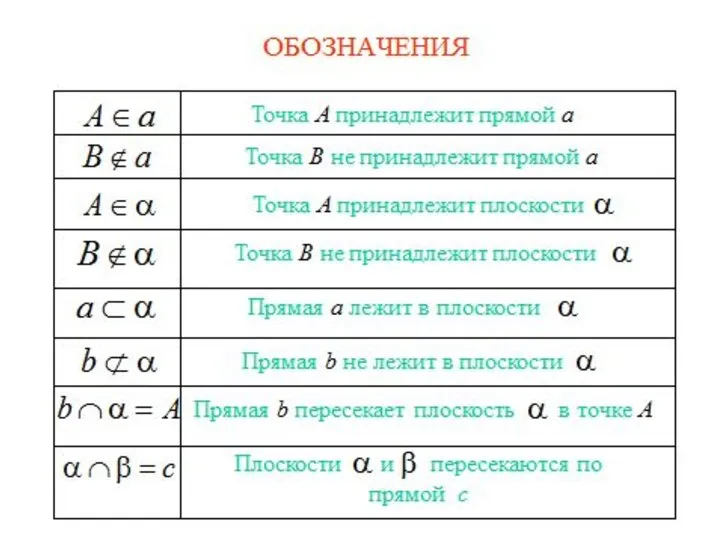
A, B, C, …
a, b, c, …
или
AВ, BС, CD, …

Аксиома
(от греч. axíõma – принятие положения)
исходное положение научной теории, принимаемое без доказательства

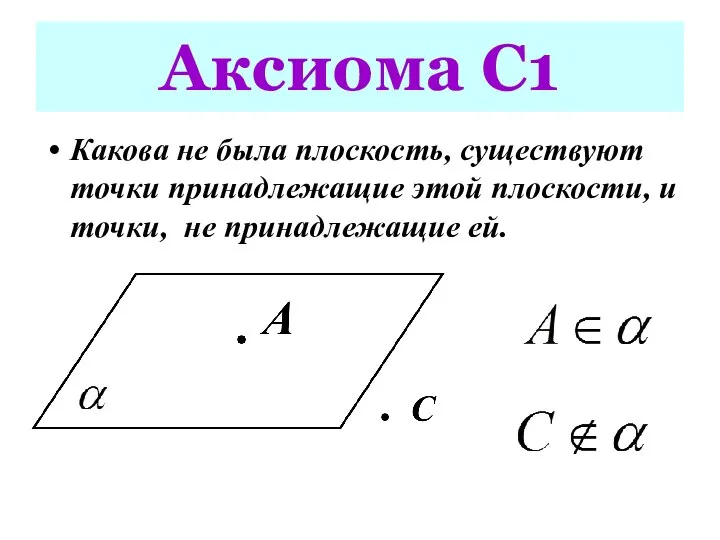
Какова не была плоскость, существуют точки принадлежащие этой плоскости, и точки, не принадлежащие ей.
Аксиома С1

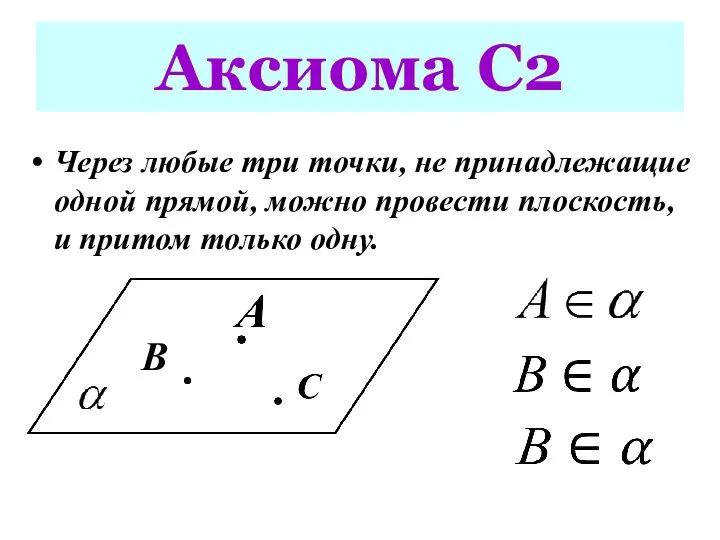
Аксиома С2
В
Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.

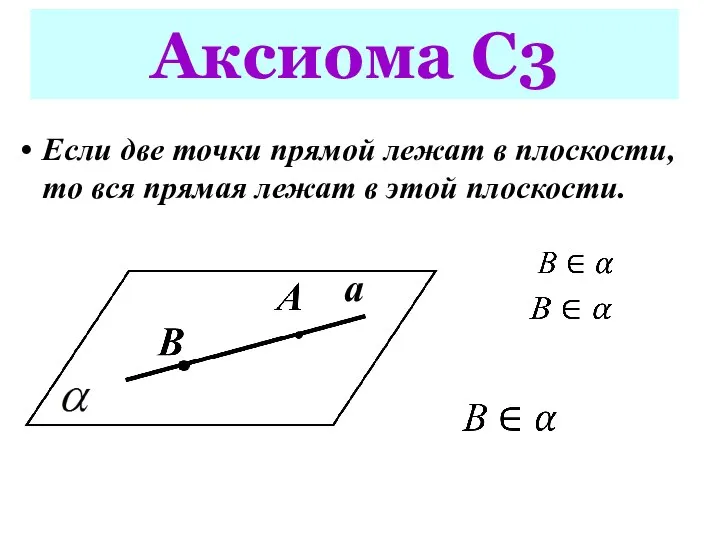
Аксиома С3
а
Если две точки прямой лежат в плоскости, то вся прямая лежат в этой плоскости.

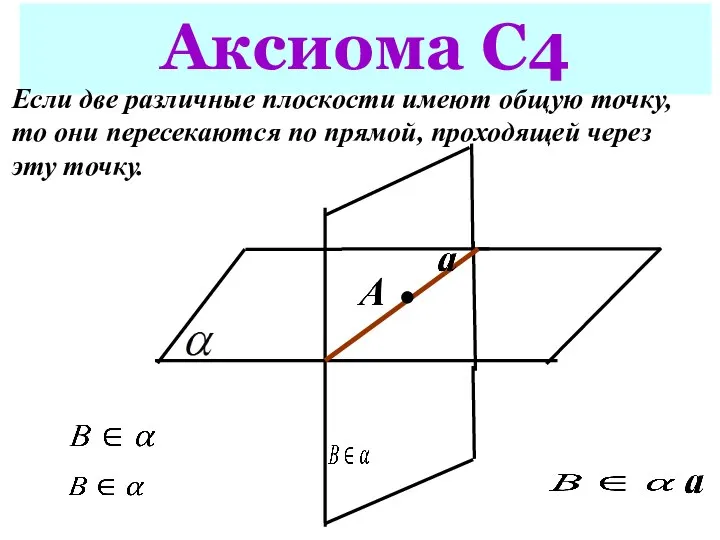
Аксиома С4
Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

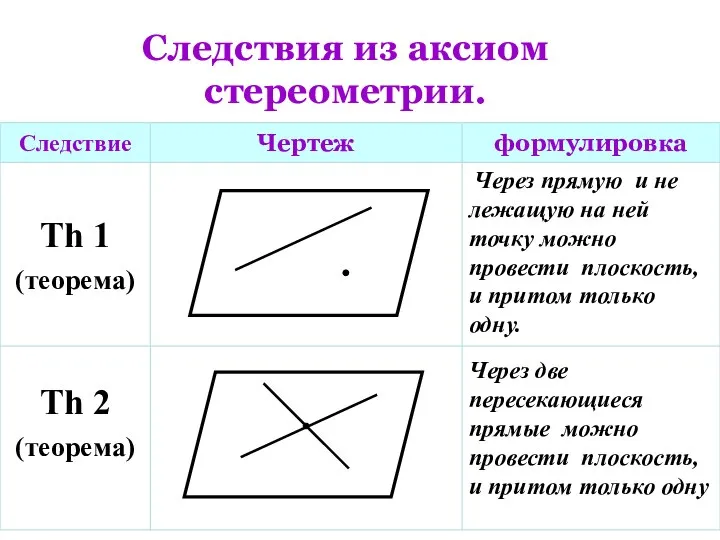
Следствия из аксиом стереометрии.
Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.
Через две пересекающиеся прямые можно провести плоскость, и притом только одну

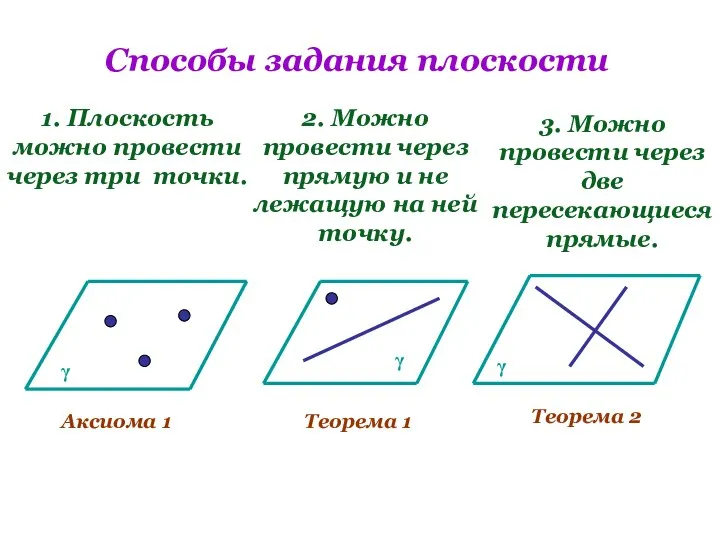
Способы задания плоскости
1. Плоскость можно провести через три точки.
2. Можно провести через прямую и не лежащую на ней точку.
Аксиома 1
Теорема 1
Теорема 2
3. Можно провести через две пересекающиеся прямые.