Содержание
- 2. Многие физические величины характеризуются числовым значением и направлением в пространстве, их называют векторными величинами
- 3. Нулевой вектор – это любая точка плоскости или пространства. Нулевым вектором называется вектор, у которого начальная
- 4. Если два вектора лежат на одной прямой или на параллельных прямых , то такие векторы называют
- 5. Если два вектора не лежат на одной прямой или на параллельных прямых , то такие векторы
- 7. Два вектора называются равными, если они сонаправленные и их длины равны.
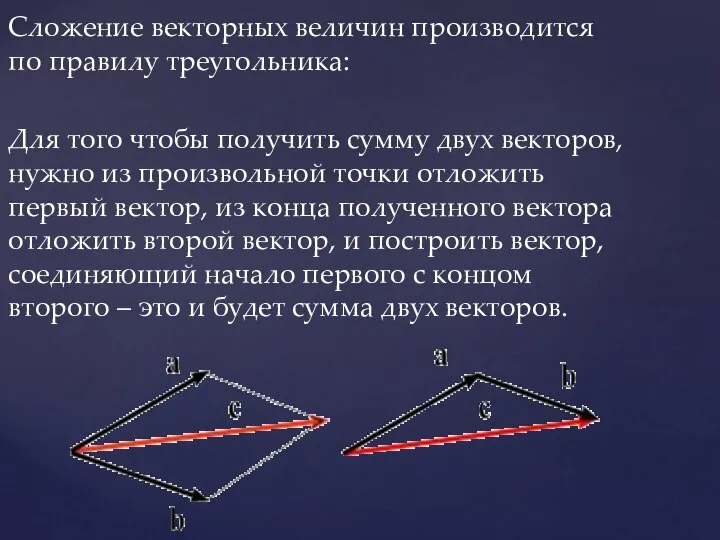
- 8. Сложение векторных величин производится по правилу треугольника: Для того чтобы получить сумму двух векторов, нужно из
- 10. Произведением вектора ? ≠ 0 на число k называется вектор, модуль которого равен числу |?|∗|? |и
- 11. Свойство вычитания суммы из числа: Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое
- 12. Свойство вычитания числа из суммы Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого,
- 13. Геометрическая интерпретация. Произведение ненулевого вектора на число - это вектор, коллинеарный данному (сонаправленный данному, если число
- 14. Формула умножения вектора на число для плоских задач В случае плоской задачи произведение вектора a =
- 15. Свойства вектора умноженного на число Если вектор b равен произведению ненулевого числа k и ненулевого вектора
- 16. Формула умножения вектора на число для плоских задач В случае плоской задачи произведение вектора a =
- 17. Свойства вектора умноженного на число Если вектор b равен произведению ненулевого числа k и ненулевого вектора
- 18. Угол между векторами.
- 19. Формула скалярного произведения векторов для плоских задач В случае плоской задачи скалярное произведение векторов a =
- 20. Скалярное произведение вектора самого на себя всегда больше или равно нуля: a · a ≥ 0
- 21. Свойство вычитания суммы из числа: Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое
- 22. Свойство вычитания числа из суммы Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого,
- 24. Скачать презентацию




















 Квадратичная функция и ее график
Квадратичная функция и ее график Классификация систем массового обслуживания
Классификация систем массового обслуживания Deterministic finite automata. Nondeterministic finite automata
Deterministic finite automata. Nondeterministic finite automata Математическая интеллектуальная игра для всей семьи
Математическая интеллектуальная игра для всей семьи urok_1_10_klass_geom
urok_1_10_klass_geom Формулы площади
Формулы площади Множество и его элементы
Множество и его элементы Статистический опрос жителей Санкт-Петербурга о применении ими пиротехнических изделий
Статистический опрос жителей Санкт-Петербурга о применении ими пиротехнических изделий Презентация на тему Приемы доказательства неравенств, содержащих переменные
Презентация на тему Приемы доказательства неравенств, содержащих переменные 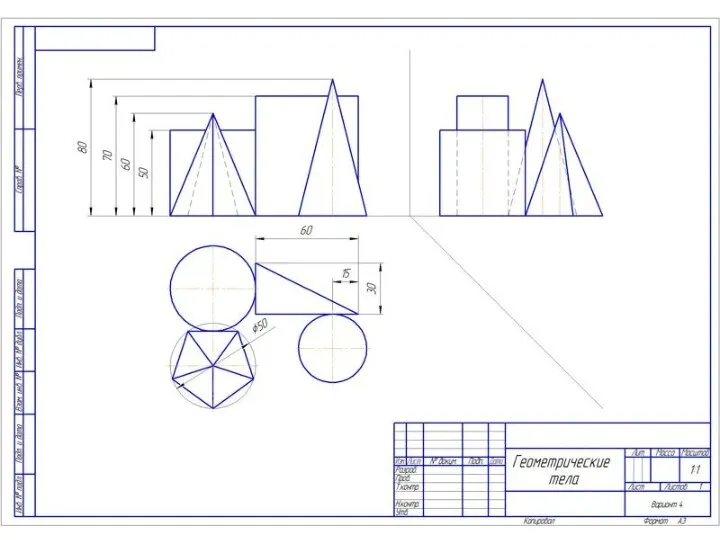 Геометрические тела. 9 класс
Геометрические тела. 9 класс Статистика оплаты труда. Статистическое изучение фонда заработной платы и фонда материального поощрения
Статистика оплаты труда. Статистическое изучение фонда заработной платы и фонда материального поощрения Режим поступления заявок
Режим поступления заявок Презентация на тему Письменное умножение на двузначное число (4 класс)
Презентация на тему Письменное умножение на двузначное число (4 класс)  Основы тригонометрии. Упражнения
Основы тригонометрии. Упражнения Римские Числа Копылова Ольга 6 класс
Римские Числа Копылова Ольга 6 класс Морское путешествие
Морское путешествие Вероятность случайного события. Математика
Вероятность случайного события. Математика Час занимательной математики
Час занимательной математики Частные случаи длины дуги. Лекция №10
Частные случаи длины дуги. Лекция №10 Законы булевой алгебры
Законы булевой алгебры Свойство описанного четырехугольника
Свойство описанного четырехугольника Производная элементарных функций
Производная элементарных функций 20140130_dekada
20140130_dekada Решение уравнений
Решение уравнений Критические точки функции
Критические точки функции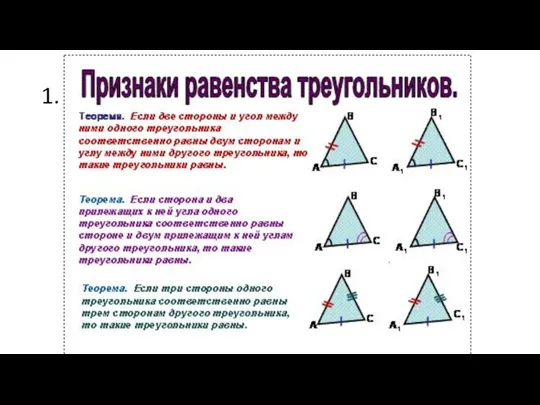 Признаки равенства треугольников
Признаки равенства треугольников Рациональные дроби и их свойства
Рациональные дроби и их свойства Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число