Содержание
- 2. По сторонам По углам равносторонний Треугольники делятся на виды: равнобедренный разносторонний прямоугольный остроугольный тупоугольный ?
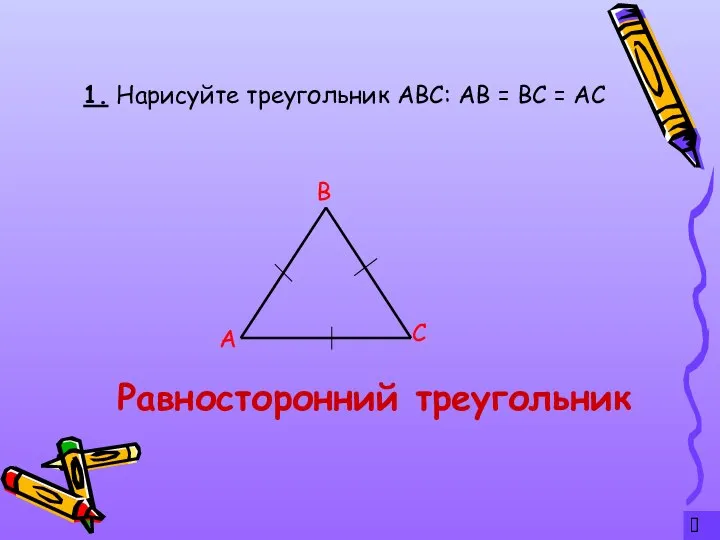
- 3. ? 1. Нарисуйте треугольник АВС: АВ = ВС = АС А С В Равносторонний треугольник
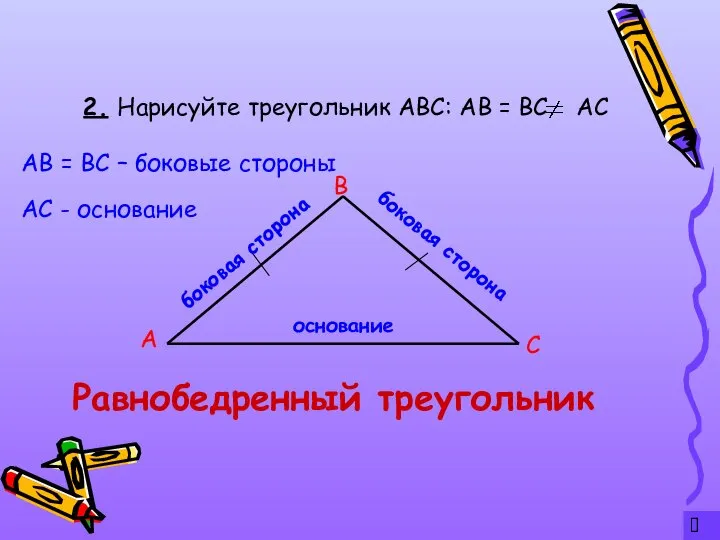
- 4. ? 2. Нарисуйте треугольник АВС: АВ = ВС АС А С В основание боковая сторона боковая
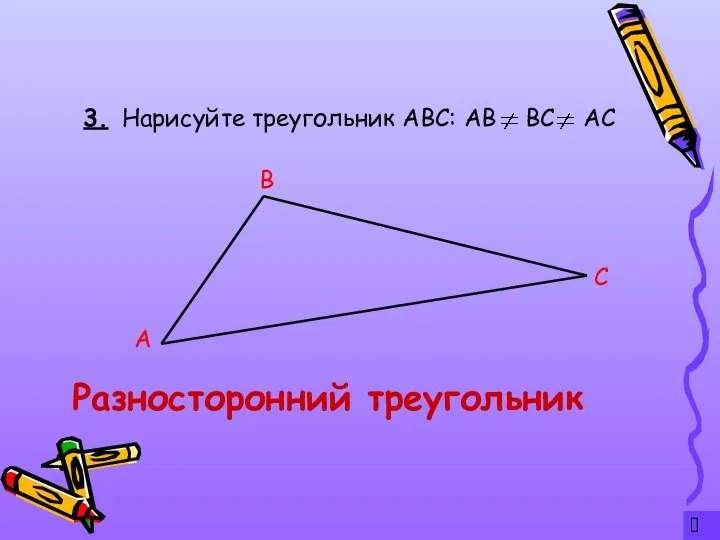
- 5. ? 3. Нарисуйте треугольник АВС: АВ ВС АС Разносторонний треугольник А С В
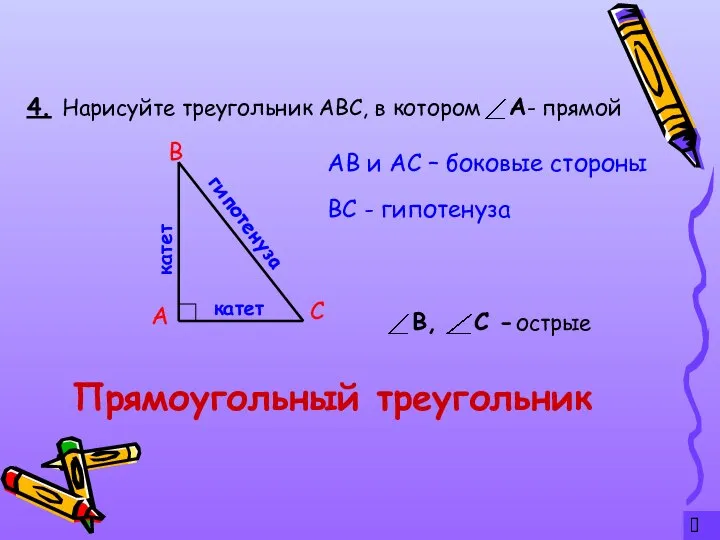
- 6. ? 4. Прямоугольный треугольник Нарисуйте треугольник АВС, в котором - прямой А С В катет катет
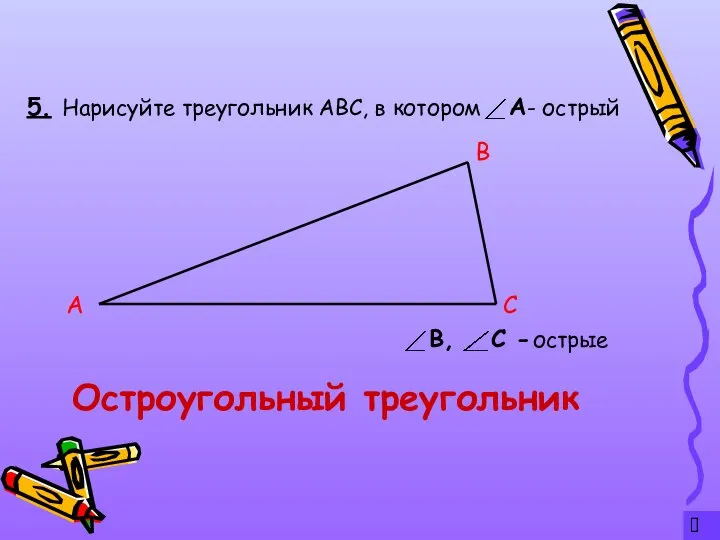
- 7. ? 5. Остроугольный треугольник Нарисуйте треугольник АВС, в котором - острый А С В острые
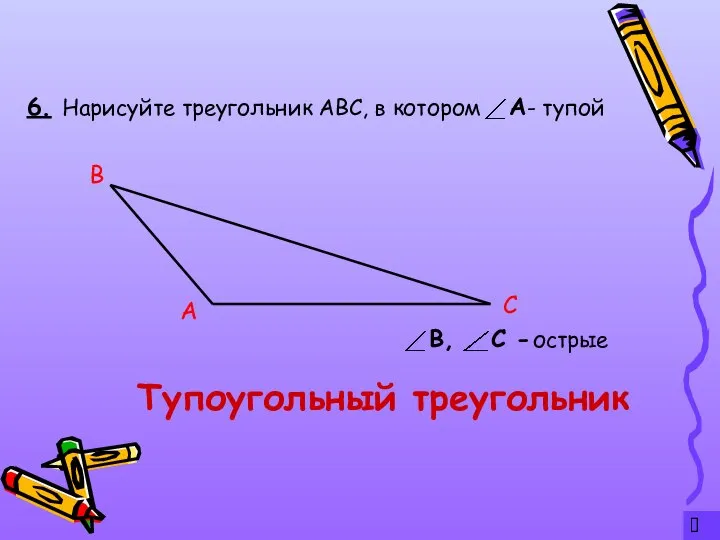
- 8. ? 6. Тупоугольный треугольник Нарисуйте треугольник АВС, в котором - тупой А С В острые
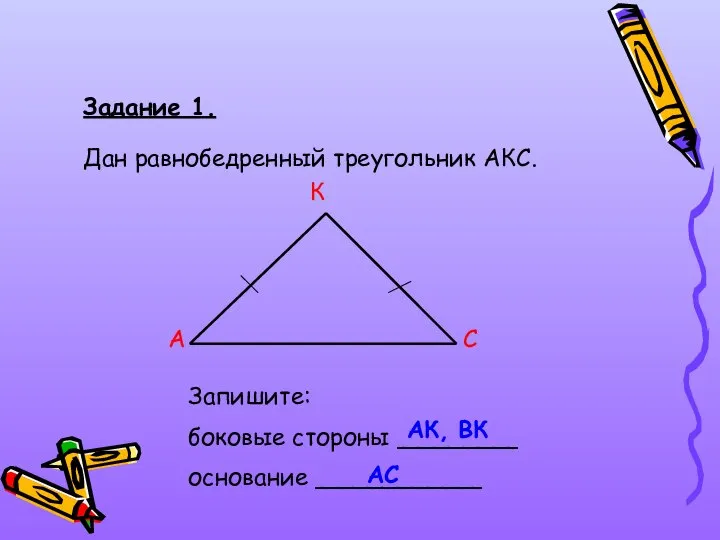
- 9. Задание 1. Дан равнобедренный треугольник АКС. А С К Запишите: боковые стороны ________ основание ___________ АК,
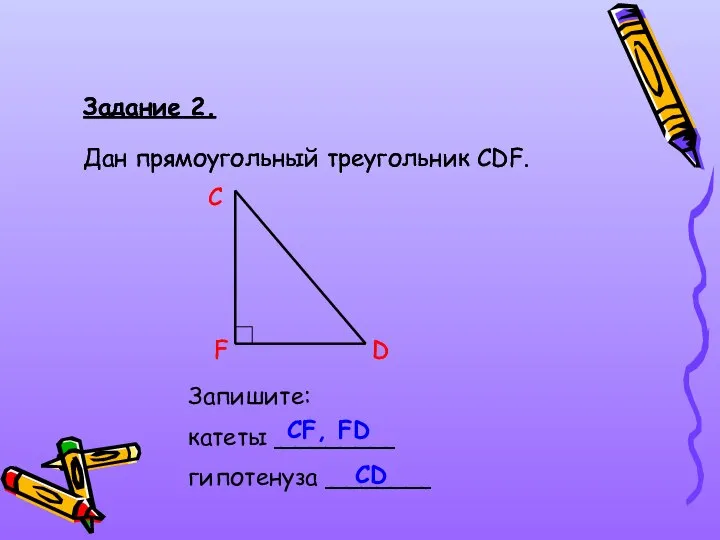
- 10. Задание 2. Дан прямоугольный треугольник СDF. C D F Запишите: катеты ________ гипотенуза _______ CF, FD
- 11. Задание 4. Верны ли утверждения: 1) Равносторонний треугольник является равнобедренным 2) Равнобедренный треугольник обязательно является остроугольным
- 12. A C B M Медианой треугольника, проведённой из данной вершины , называется отрезок , соединяющий эту
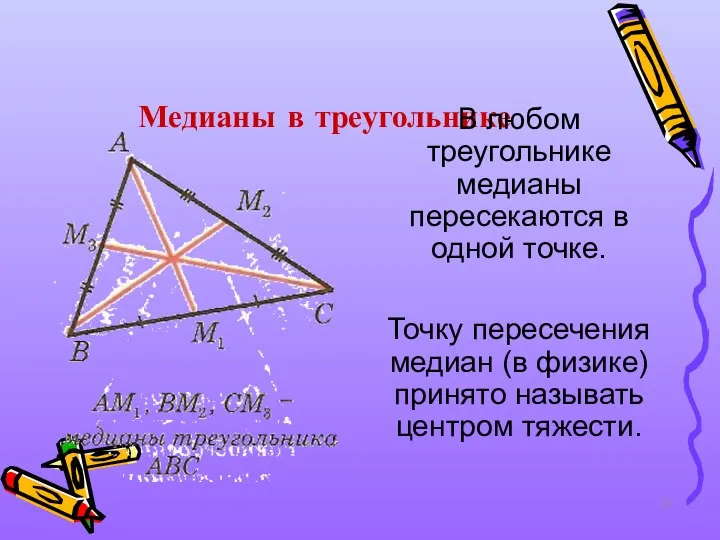
- 13. Медианы в треугольнике В любом треугольнике медианы пересекаются в одной точке. Точку пересечения медиан (в физике)
- 14. Медиана – обезьяна, У которой зоркий глаз. Прыгнет точно в середину Стороны против вершины, Где находится
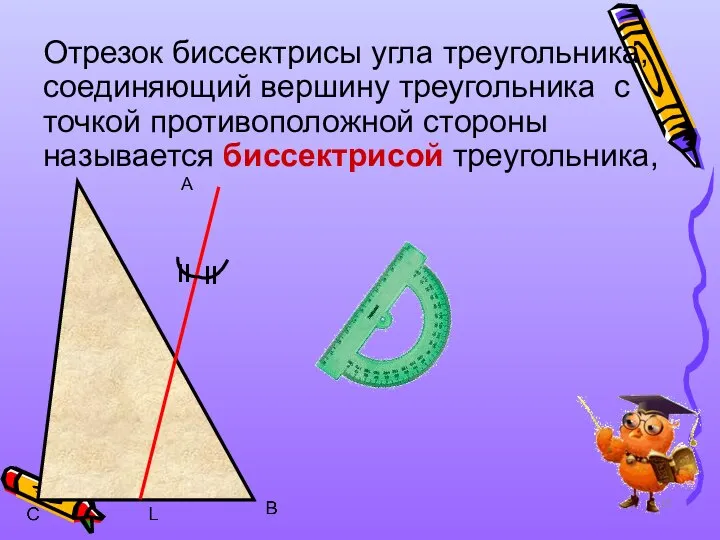
- 15. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны называется биссектрисой треугольника, A
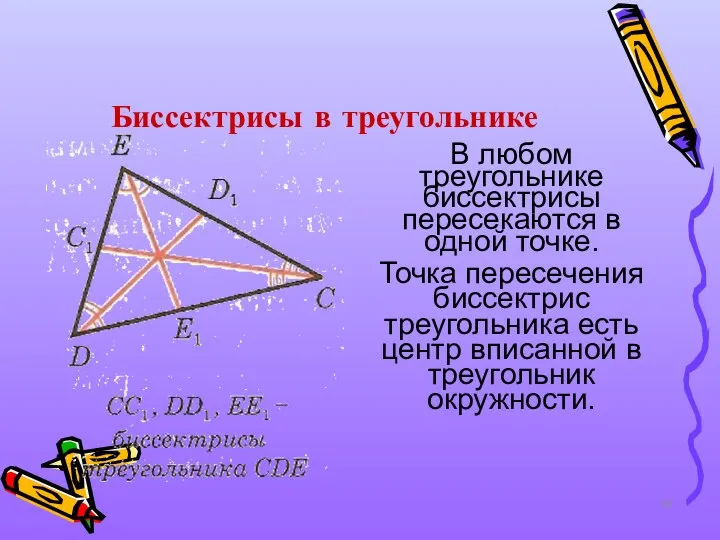
- 16. Биссектрисы в треугольнике В любом треугольнике биссектрисы пересекаются в одной точке. Точка пересечения биссектрис треугольника есть
- 17. Биссектриса - это крыса. Которая бегает по углам И делит угол пополам.
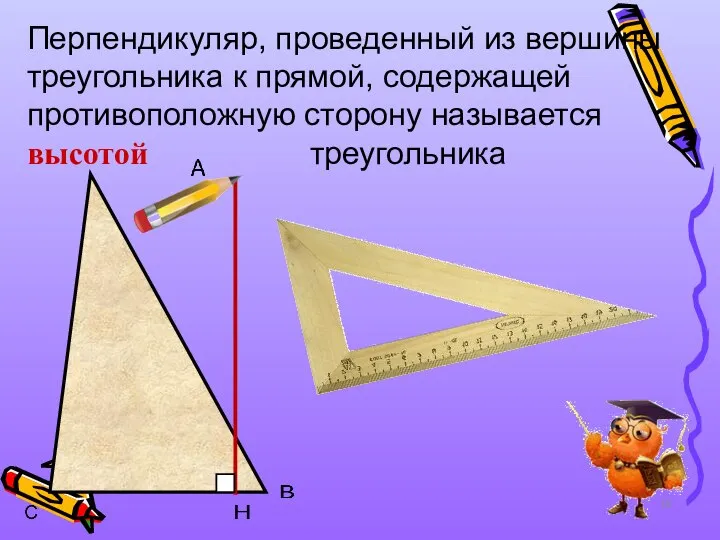
- 18. Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону называется высотой треугольника
- 19. Высота похожа на кота. Который, выгнув спину И под прямым углом Соединит вершину И сторону хвостом,
- 21. Скачать презентацию






 Решение квадратных уравнений
Решение квадратных уравнений Длина окружности
Длина окружности Лічба в межах 20. Складання і розв’язування задач на знаходження суми й остачі. Побудова відрізків заданої довжини
Лічба в межах 20. Складання і розв’язування задач на знаходження суми й остачі. Побудова відрізків заданої довжини Геометрическое решение задачи о расстояниях между точками
Геометрическое решение задачи о расстояниях между точками Индивидуальный проект на тему Золотое сечение в природе
Индивидуальный проект на тему Золотое сечение в природе Признаки равенства треугольников
Признаки равенства треугольников Решение задач с помощью уравнений. 7 класс
Решение задач с помощью уравнений. 7 класс Теорія множин. Відношення
Теорія множин. Відношення Числовые выражения
Числовые выражения Презентация на тему Сечения
Презентация на тему Сечения  Презентация на тему ЛОГАРИФМЫ И ИХ СВОЙСТВА
Презентация на тему ЛОГАРИФМЫ И ИХ СВОЙСТВА  Теорема о рациональном корне многочлена с целыми коэффициентами
Теорема о рациональном корне многочлена с целыми коэффициентами Комбинаторика
Комбинаторика Вероятность и статистика
Вероятность и статистика Математические игры
Математические игры Презентация на тему Призма: виды и особенности
Презентация на тему Призма: виды и особенности 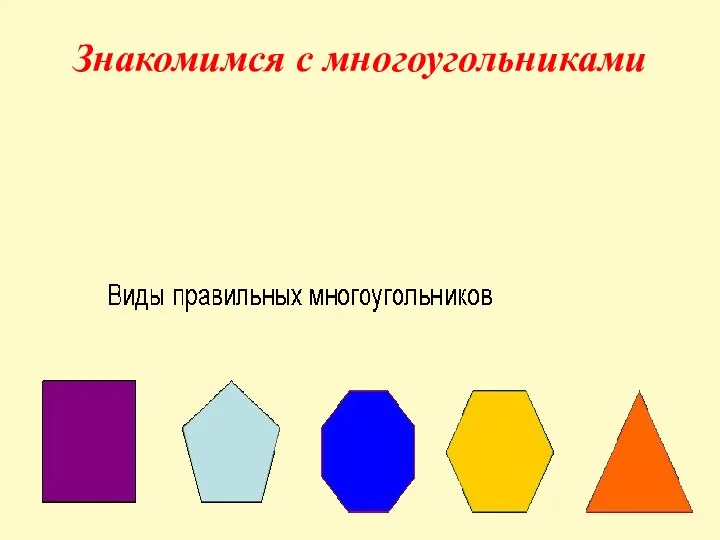 Знакомимся с многоугольниками
Знакомимся с многоугольниками Aproximarea numerică a funcţiilor. Metode numerice – curs 11
Aproximarea numerică a funcţiilor. Metode numerice – curs 11 Тренажёр Теремок. Математика - 1 класс
Тренажёр Теремок. Математика - 1 класс P-ичная арифметика. Решение задач
P-ичная арифметика. Решение задач Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Площадь треугольника
Площадь треугольника Перпендикулярные прямые
Перпендикулярные прямые Арифметический корень степени п
Арифметический корень степени п Нумерация. Подготовка к ВПР
Нумерация. Подготовка к ВПР Динамика нелинейного тентообразного отображения с параметром
Динамика нелинейного тентообразного отображения с параметром Скрипт параллелограм
Скрипт параллелограм Занятие 1. Вводное занятие
Занятие 1. Вводное занятие