Содержание
- 2. 1. Основные понятия теории графов
- 3. ДУГА {A,B} Ориентированный Граф G(V,E) A B D C ВЕРШИНА D ДУГА {B,A} ЦИКЛ (Петля) МНОЖЕСТВО
- 4. Неориентированный Граф G(V,E) A B D C ВЕРШИНА А (B,A)=(A,B) МНОЖЕСТВО ВЕРШИН МНОЖЕСТВО РЕБЕР РЕБРО (A,B)
- 5. Ориентированные и неориентированные графы Ориентированный граф G(V,E), V = {1,2,3,4,5,6} E = {{1,2}, {2,2}, {2,4}, {2,5},
- 6. Основные понятия Вершина графа Смежная Изолированная Висячая Степень вершины исходящая, входящая Ребро (дуга) графа Инцидентность вес
- 7. Пути и циклы в графе A B D C E G H I J F
- 8. Изоморфизм графов ИЗОМОРФНЫЕ ГРАФЫ НЕИЗОМОРФНЫЕ ГРАФЫ
- 9. Подграфы A B D C E A B D C E G(V,E) G’(V’,E’) G’ подграф G,
- 10. Клики в графе A B D C E F G
- 11. Двудольные графы A B D C E F G
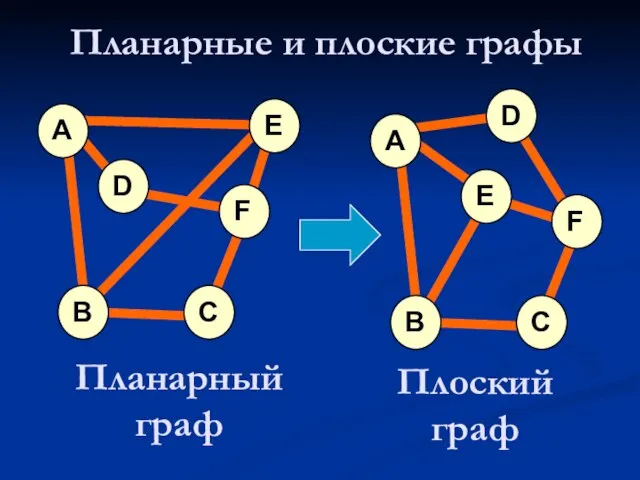
- 12. Планарные и плоские графы A B D C E F A B D C E F
- 13. 2. Алгоритмы на графах
- 14. Минимальные покрывающие деревья Имеется граф G(V,E) Каждому ребру (u,v) задан неотрицательный вес w(u,v) Задача: найти подмножество
- 15. Отличия теории и практики A B C D A B C D A B C D
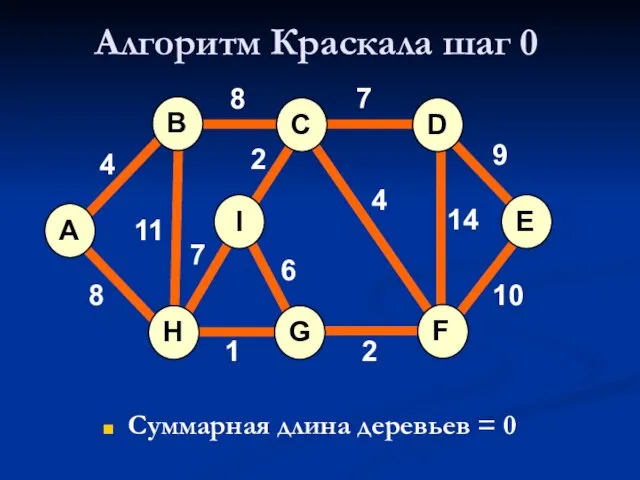
- 16. Алгоритм Краскала шаг 0 Суммарная длина деревьев = 0 A H G I B F C
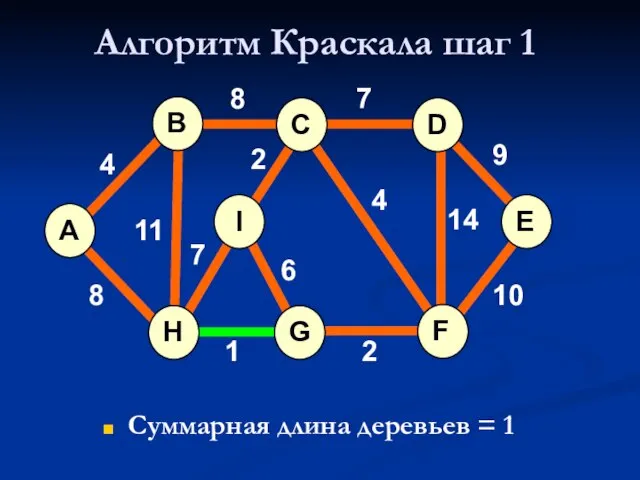
- 17. Алгоритм Краскала шаг 1 Суммарная длина деревьев = 1 A H G I B F C
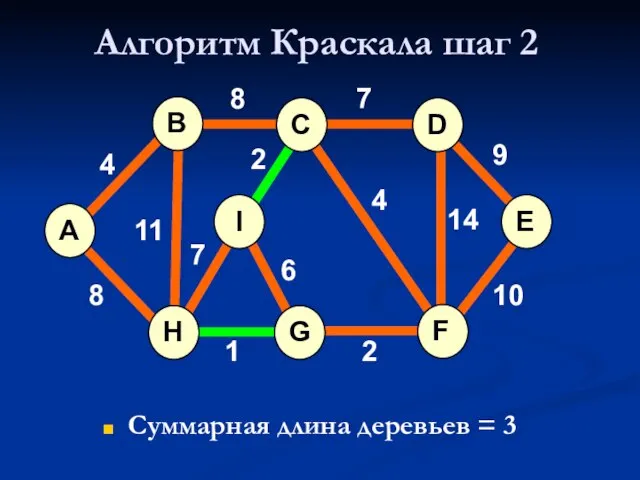
- 18. Алгоритм Краскала шаг 2 Суммарная длина деревьев = 3 A H G I B F C
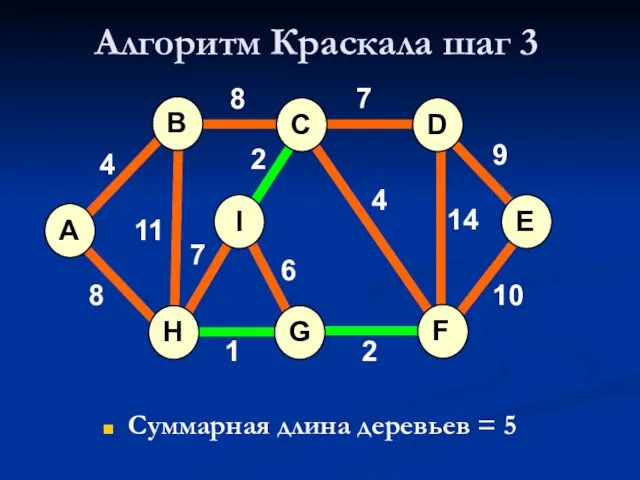
- 19. Алгоритм Краскала шаг 3 Суммарная длина деревьев = 5 A H G I B F C
- 20. Алгоритм Краскала шаг 4 Суммарная длина деревьев = 9 A H G I B F C
- 21. Алгоритм Краскала шаг 5 Суммарная длина деревьев = 13 A H G I B F C
- 22. Алгоритм Краскала шаг 6 Суммарная длина деревьев = 20 A H G I B F C
- 23. Алгоритм Краскала шаг 7 Суммарная длина деревьев = 28 A H G I B F C
- 24. Алгоритм Краскала шаг 8 Суммарная длина деревьев = 37 A H G I B F C
- 25. Алгоритм Краскала шаг 9 Суммарная длина деревьев = 37 A H G I B F C
- 26. Алгоритм Прима Начало алгоритма: с произвольной вершины К текущему дереву присоединяется смежная вершина с кратчайшим ребром.
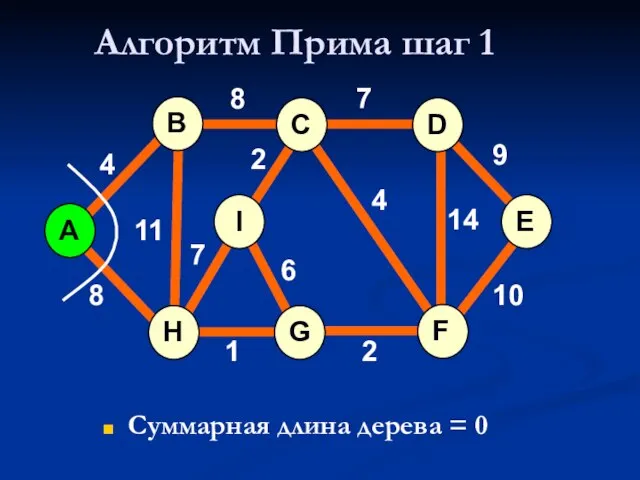
- 27. Алгоритм Прима шаг 0 Суммарная длина дерева = 0 A H G I B F C
- 28. Алгоритм Прима шаг 1 Суммарная длина дерева = 0 A H G I B F C
- 29. Алгоритм Прима шаг 2 Суммарная длина дерева = 4 A H G I B F C
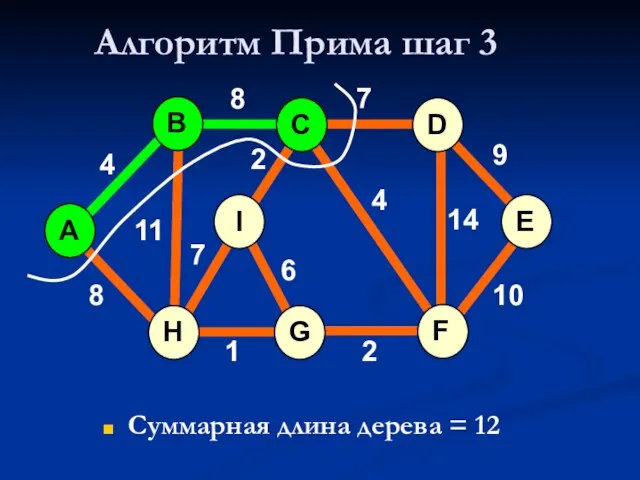
- 30. Алгоритм Прима шаг 3 Суммарная длина дерева = 12 A H G I B F C
- 31. Алгоритм Прима шаг 4 Суммарная длина дерева = 14 A H G I B F C
- 32. Алгоритм Прима шаг 5 Суммарная длина дерева = 18 A H G I B F C
- 33. Алгоритм Прима шаг 6 Суммарная длина дерева = 20 A H G I B F C
- 34. Алгоритм Прима шаг 7 Суммарная длина дерева = 21 A H G I B F C
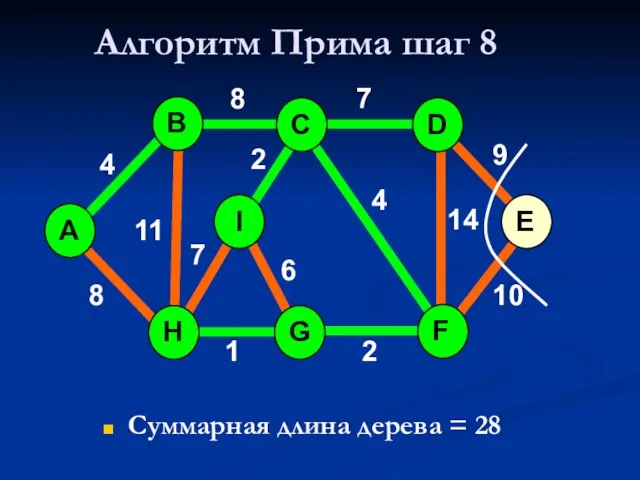
- 35. Алгоритм Прима шаг 8 Суммарная длина дерева = 28 A H G I B F C
- 36. Алгоритм Прима шаг 9 Суммарная длина дерева = 37 A H G I B F C
- 37. Алгоритм Прима шаг 10 Суммарная длина дерева = 37 A H G I B F C
- 38. КРАТЧАЙШИЕ ПУТИ В ГРАФЕ Алгоритм Дейкстры (Дийкстры) Алгоритм Ли Алгоритм А* (А-звездочка)
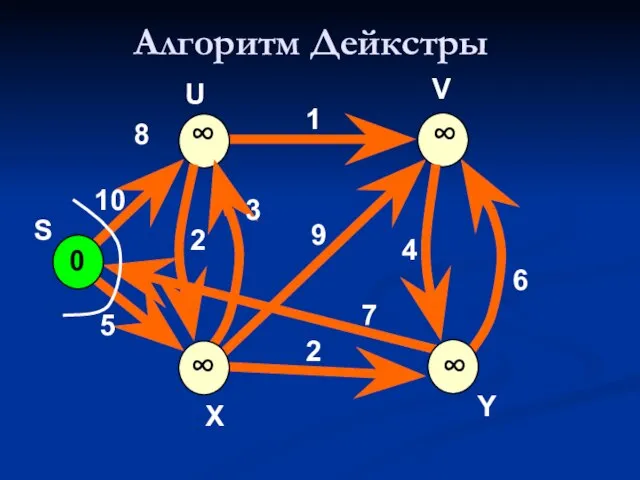
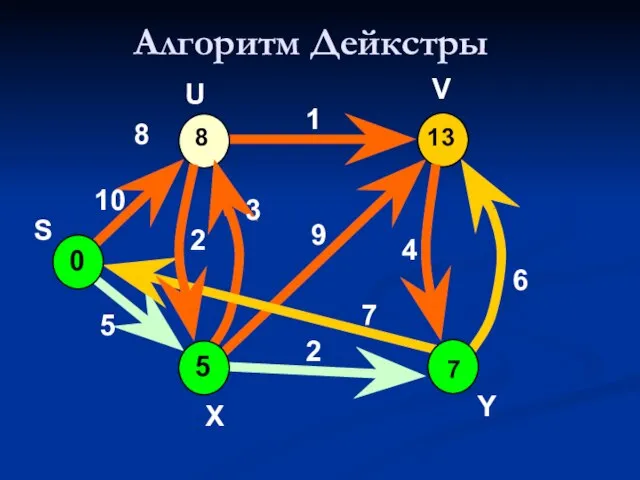
- 39. Алгоритм Дейкстры 0 ∞ V 10 5 7 2 9 1 8 4 6 U S
- 40. Алгоритм Дейкстры 0 V 10 5 7 2 9 1 8 4 6 U S X
- 41. Алгоритм Дейкстры 0 V 10 5 7 2 9 1 8 4 6 U S X
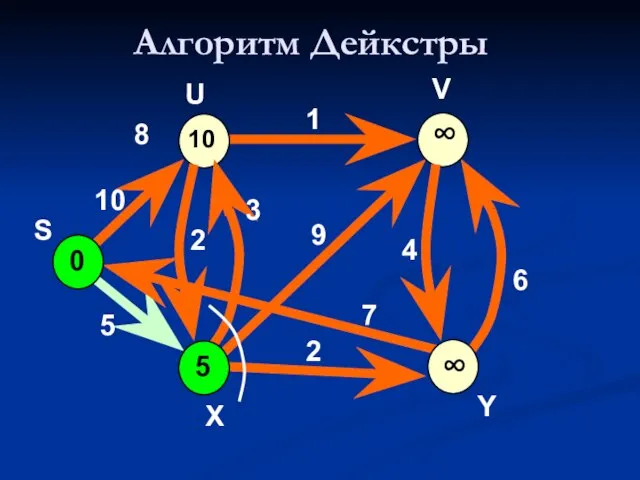
- 42. Алгоритм Дейкстры 0 10 V 10 5 7 2 9 1 8 4 6 U S
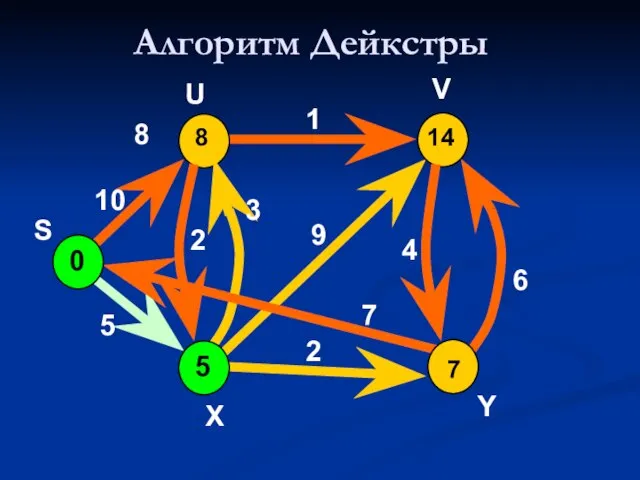
- 43. Алгоритм Дейкстры 0 8 V 10 5 7 2 9 1 8 4 6 U S
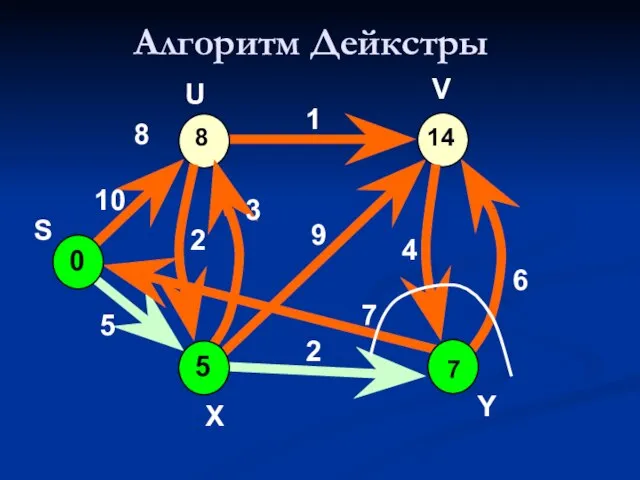
- 44. Алгоритм Дейкстры 0 8 V 10 5 7 2 9 1 8 4 6 U S
- 45. Алгоритм Дейкстры 0 8 V 10 5 7 2 9 1 8 4 6 U S
- 46. Алгоритм Дейкстры 0 8 V 10 5 7 2 9 1 8 4 6 U S
- 47. Алгоритм Дейкстры 0 8 V 10 5 7 2 9 1 8 4 6 U S
- 48. Алгоритм А* (Алгоритм оптимального поиска) S V’ V F 9 11 g(v) h(v) F(v)=g(v)+h(v)
- 49. Оценка длины пути Точная длина Минимальная оценка Манхеттеновская длина
- 50. Алгоритм А* g(v) – стоимость пути от финиша до вершины v. h(v) – нижняя оценка стоимости
- 52. Скачать презентацию




































 Урок математики. Длины
Урок математики. Длины элементы теории множеств
элементы теории множеств Определение равнодействующей и уравновешивающих сходящихся сил плоской системы сил графическим и аналитическим способами
Определение равнодействующей и уравновешивающих сходящихся сил плоской системы сил графическим и аналитическим способами Презентация на тему Решение уравнений и неравенств, содержащих модуль
Презентация на тему Решение уравнений и неравенств, содержащих модуль  Решение уравнений с помощью разложения на множители
Решение уравнений с помощью разложения на множители Свойства сторон и углов треугольника
Свойства сторон и углов треугольника Урок повторения
Урок повторения Инфекционные заболевания с кожным симптомом
Инфекционные заболевания с кожным симптомом Worksheet 3 (reatke)
Worksheet 3 (reatke) Основные формулы для Огэ по математике
Основные формулы для Огэ по математике Синтаксис объявления функции
Синтаксис объявления функции Устный счёт
Устный счёт Презентация на тему Математические диктанты 3 класс
Презентация на тему Математические диктанты 3 класс  Тригонометрические уравнения. Устный счет
Тригонометрические уравнения. Устный счет 20f
20f Числа, кратные 3
Числа, кратные 3 Формула Эйлера для расстояния между центрами вписанной и описанной окружностей треугольника
Формула Эйлера для расстояния между центрами вписанной и описанной окружностей треугольника Мера Лебега
Мера Лебега Случаи вычитания 11-
Случаи вычитания 11- Неравенства с двумя переменными и их системы
Неравенства с двумя переменными и их системы Відео. Задача на 2 дії
Відео. Задача на 2 дії Прямопропорциональные величины
Прямопропорциональные величины Расстояние между точками с заданными координатами. Координаты середины отрезка
Расстояние между точками с заданными координатами. Координаты середины отрезка Организация исследовательской деятельности учащихся по математике
Организация исследовательской деятельности учащихся по математике Математика. Управление социальными системами. Математический анализ. Дифференцирование функции одной переменной
Математика. Управление социальными системами. Математический анализ. Дифференцирование функции одной переменной interactive english. Missing Santa. Math
interactive english. Missing Santa. Math Сводка и группировка
Сводка и группировка Презентация на тему Делимое и делитель (2 класс)
Презентация на тему Делимое и делитель (2 класс)